Ultra Fast PDE Solving via Physics Guided Few-step Diffusion

Diffusion-based models have demonstrated impressive accuracy and generalization in solving partial differential equations (PDEs). However, they still face significant limitations, such as high sampling costs and insufficient physical consistency, stemming from their many-step iterative sampling mechanism and lack of explicit physics constraints. To address these issues, we propose Phys-Instruct, a novel physics-guided distillation framework which not only (1) compresses a pre-trained diffusion PDE solver into a few-step generator via matching generator and prior diffusion distributions to enable rapid sampling, but also (2) enhances the physics consistency by explicitly injecting PDE knowledge through a PDE distillation guidance. Physic-Instruct is built upon a solid theoretical foundation, leading to a practical physics-constrained training objective that admits tractable gradients. Across five PDE benchmarks, Phys-Instruct achieves orders-of-magnitude faster inference while reducing PDE error by more than 8 times compared to state-of-the-art diffusion baselines. Moreover, the resulting unconditional student model functions as a compact prior, enabling efficient and physically consistent inference for various downstream conditional tasks. Our results indicate that Phys-Instruct is a novel, effective, and efficient framework for ultra-fast PDE solving powered by deep generative models.

ATLAS : Adaptive Self-Evolutionary Research Agent with Task-Distributed Multi-LLM Supporters

Recent multi-LLM agent systems perform well in prompt optimization and automated problem-solving, but many either keep the solver frozen after fine-tuning or rely on a static preference-optimization loop, which becomes intractable for long-horizon tasks. We propose ATLAS (Adaptive Task-distributed Learning for Agentic Self-evolution), a task-distributed framework that iteratively develops a lightweight research agent while delegating complementary roles to specialized supporter agents for exploration, hyperparameter tuning, and reference policy management. Our core algorithm, Evolving Direct Preference Optimization (EvoDPO), adaptively updates the phase-indexed reference policy. We provide a theoretical regret analysis for a preference-based contextual bandit under concept drift. In addition, experiments were conducted on non-stationary linear contextual bandits and scientific machine learning (SciML) loss reweighting for the 1D Burgers' equation. Both results show that ATLAS improves stability and performance over a static single-agent baseline.

Task-tailored Pre-processing: Fair Downstream Supervised Learning

Fairness-aware machine learning has recently attracted various communities to mitigate discrimination against certain societal groups in data-driven tasks. For fair supervised learning, particularly in pre-processing, there have been two main categories: data fairness and task-tailored fairness. The former directly finds an intermediate distribution among the groups, independent of the type of the downstream model, so a learned downstream classification/regression model returns similar predictive scores to individuals inputting the same covariates irrespective of their sensitive attributes. The latter explicitly takes the supervised learning task into account when constructing the pre-processing map. In this work, we study algorithmic fairness for supervised learning and argue that the data fairness approaches impose overly strong regularization from the perspective of the HGR correlation. This motivates us to devise a novel pre-processing approach tailored to supervised learning. We account for the trade-off between fairness and utility in obtaining the pre-processing map. Then we study the behavior of arbitrary downstream supervised models learned on the transformed data to find sufficient conditions to guarantee their fairness improvement and utility preservation. To our knowledge, no prior work in the branch of task-tailored methods has theoretically investigated downstream guarantees when using pre-processed data. We further evaluate our framework through comparison studies based on tabular and image data sets, showing the superiority of our framework which preserves consistent trade-offs among multiple downstream models compared to recent competing models. Particularly for computer vision data, we see our method alters only necessary semantic features related to the central machine learning task to achieve fairness.

ICP-4D: Bridging Iterative Closest Point and LiDAR Panoptic Segmentation

Dominant paradigms for 4D LiDAR panoptic segmentation are usually required to train deep neural networks with large superimposed point clouds or design dedicated modules for instance association. However, these approaches perform redundant point processing and consequently become computationally expensive, yet still overlook the rich geometric priors inherently provided by raw point clouds. To this end, we introduce ICP-4D, a simple yet effective training-free framework that unifies spatial and temporal reasoning through geometric relations among instance-level point sets. Specifically, we apply the Iterative Closest Point (ICP) algorithm to directly associate temporally consistent instances by aligning the source and target point sets through the estimated transformation. To stabilize association under noisy instance predictions, we introduce a Sinkhorn-based soft matching. This exploits the underlying instance distribution to obtain accurate point-wise correspondences, resulting in robust geometric alignment. Furthermore, our carefully designed pipeline, which considers three instance types-static, dynamic, and missing-offers computational efficiency and occlusion-aware matching. Our extensive experiments across both SemanticKITTI and panoptic nuScenes demonstrate that our method consistently outperforms state-of-the-art approaches, even without additional training or extra point cloud inputs.

Rethinking Langevin Thompson Sampling from A Stochastic Approximation Perspective

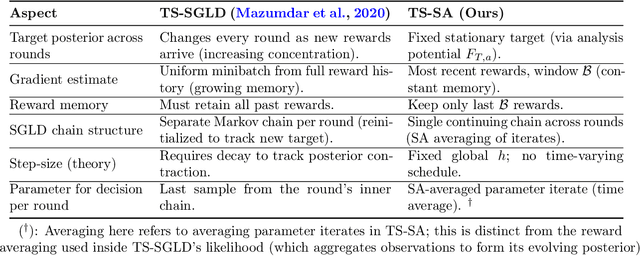
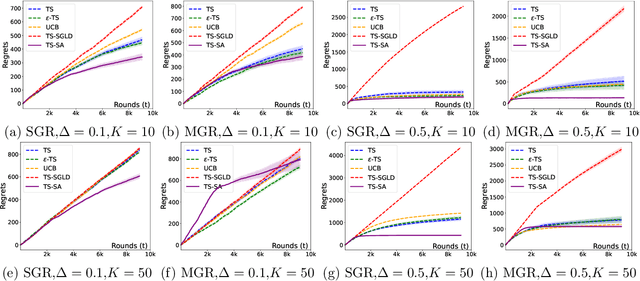
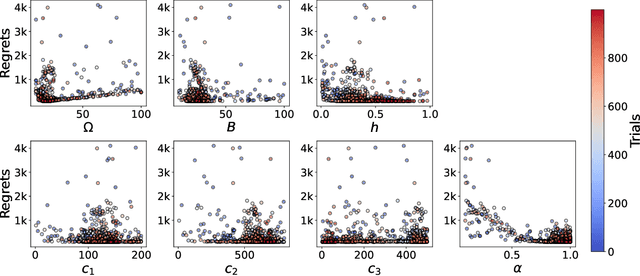
Most existing approximate Thompson Sampling (TS) algorithms for multi-armed bandits use Stochastic Gradient Langevin Dynamics (SGLD) or its variants in each round to sample from the posterior, relaxing the need for conjugacy assumptions between priors and reward distributions in vanilla TS. However, they often require approximating a different posterior distribution in different round of the bandit problem. This requires tricky, round-specific tuning of hyperparameters such as dynamic learning rates, causing challenges in both theoretical analysis and practical implementation. To alleviate this non-stationarity, we introduce TS-SA, which incorporates stochastic approximation (SA) within the TS framework. In each round, TS-SA constructs a posterior approximation only using the most recent reward(s), performs a Langevin Monte Carlo (LMC) update, and applies an SA step to average noisy proposals over time. This can be interpreted as approximating a stationary posterior target throughout the entire algorithm, which further yields a fixed step-size, a unified convergence analysis framework, and improved posterior estimates through temporal averaging. We establish near-optimal regret bounds for TS-SA, with a simplified and more intuitive theoretical analysis enabled by interpreting the entire algorithm as a simulation of a stationary SGLD process. Our empirical results demonstrate that even a single-step Langevin update with certain warm-up outperforms existing methods substantially on bandit tasks.

Physics Informed Constrained Learning of Dynamics from Static Data

A physics-informed neural network (PINN) models the dynamics of a system by integrating the governing physical laws into the architecture of a neural network. By enforcing physical laws as constraints, PINN overcomes challenges with data scarsity and potentially high dimensionality. Existing PINN frameworks rely on fully observed time-course data, the acquisition of which could be prohibitive for many systems. In this study, we developed a new PINN learning paradigm, namely Constrained Learning, that enables the approximation of first-order derivatives or motions using non-time course or partially observed data. Computational principles and a general mathematical formulation of Constrained Learning were developed. We further introduced MPOCtrL (Message Passing Optimization-based Constrained Learning) an optimization approach tailored for the Constrained Learning framework that strives to balance the fitting of physical models and observed data. Its code is available at github link: https://github.com/ptdang1001/MPOCtrL Experiments on synthetic and real-world data demonstrated that MPOCtrL can effectively detect the nonlinear dependency between observed data and the underlying physical properties of the system. In particular, on the task of metabolic flux analysis, MPOCtrL outperforms all existing data-driven flux estimators.

Conformalized-KANs: Uncertainty Quantification with Coverage Guarantees for Kolmogorov-Arnold Networks (KANs) in Scientific Machine Learning

This paper explores uncertainty quantification (UQ) methods in the context of Kolmogorov-Arnold Networks (KANs). We apply an ensemble approach to KANs to obtain a heuristic measure of UQ, enhancing interpretability and robustness in modeling complex functions. Building on this, we introduce Conformalized-KANs, which integrate conformal prediction, a distribution-free UQ technique, with KAN ensembles to generate calibrated prediction intervals with guaranteed coverage. Extensive numerical experiments are conducted to evaluate the effectiveness of these methods, focusing particularly on the robustness and accuracy of the prediction intervals under various hyperparameter settings. We show that the conformal KAN predictions can be applied to recent extensions of KANs, including Finite Basis KANs (FBKANs) and multifideilty KANs (MFKANs). The results demonstrate the potential of our approaches to improve the reliability and applicability of KANs in scientific machine learning.

Coefficient-to-Basis Network: A Fine-Tunable Operator Learning Framework for Inverse Problems with Adaptive Discretizations and Theoretical Guarantees

We propose a Coefficient-to-Basis Network (C2BNet), a novel framework for solving inverse problems within the operator learning paradigm. C2BNet efficiently adapts to different discretizations through fine-tuning, using a pre-trained model to significantly reduce computational cost while maintaining high accuracy. Unlike traditional approaches that require retraining from scratch for new discretizations, our method enables seamless adaptation without sacrificing predictive performance. Furthermore, we establish theoretical approximation and generalization error bounds for C2BNet by exploiting low-dimensional structures in the underlying datasets. Our analysis demonstrates that C2BNet adapts to low-dimensional structures without relying on explicit encoding mechanisms, highlighting its robustness and efficiency. To validate our theoretical findings, we conducted extensive numerical experiments that showcase the superior performance of C2BNet on several inverse problems. The results confirm that C2BNet effectively balances computational efficiency and accuracy, making it a promising tool to solve inverse problems in scientific computing and engineering applications.

Active operator learning with predictive uncertainty quantification for partial differential equations

In this work, we develop a method for uncertainty quantification in deep operator networks (DeepONets) using predictive uncertainty estimates calibrated to model errors observed during training. The uncertainty framework operates using a single network, in contrast to existing ensemble approaches, and introduces minimal overhead during training and inference. We also introduce an optimized implementation for DeepONet inference (reducing evaluation times by a factor of five) to provide models well-suited for real-time applications. We evaluate the uncertainty-equipped models on a series of partial differential equation (PDE) problems, and show that the model predictions are unbiased, non-skewed, and accurately reproduce solutions to the PDEs. To assess how well the models generalize, we evaluate the network predictions and uncertainty estimates on in-distribution and out-of-distribution test datasets. We find the predictive uncertainties accurately reflect the observed model errors over a range of problems with varying complexity; simpler out-of-distribution examples are assigned low uncertainty estimates, consistent with the observed errors, while more complex out-of-distribution examples are properly assigned higher uncertainties. We also provide a statistical analysis of the predictive uncertainties and verify that these estimates are well-aligned with the observed error distributions at the tail-end of training. Finally, we demonstrate how predictive uncertainties can be used within an active learning framework to yield improvements in accuracy and data-efficiency for outer-loop optimization procedures.

LAPD: Langevin-Assisted Bayesian Active Learning for Physical Discovery

Discovering physical laws from data is a fundamental challenge in scientific research, particularly when high-quality data are scarce or costly to obtain. Traditional methods for identifying dynamical systems often struggle with noise sensitivity, inefficiency in data usage, and the inability to quantify uncertainty effectively. To address these challenges, we propose Langevin-Assisted Active Physical Discovery (LAPD), a Bayesian framework that integrates replica-exchange stochastic gradient Langevin Monte Carlo to simultaneously enable efficient system identification and robust uncertainty quantification (UQ). By balancing gradient-driven exploration in coefficient space and generating an ensemble of candidate models during exploitation, LAPD achieves reliable, uncertainty-aware identification with noisy data. In the face of data scarcity, the probabilistic foundation of LAPD further promotes the integration of active learning (AL) via a hybrid uncertainty-space-filling acquisition function. This strategy sequentially selects informative data to reduce data collection costs while maintaining accuracy. We evaluate LAPD on diverse nonlinear systems such as the Lotka-Volterra, Lorenz, Burgers, and Convection-Diffusion equations, demonstrating its robustness with noisy and limited data as well as superior uncertainty calibration compared to existing methods. The AL extension reduces the required measurements by around 60% for the Lotka-Volterra system and by around 40% for Burgers' equation compared to random data sampling, highlighting its potential for resource-constrained experiments. Our framework establishes a scalable, uncertainty-aware methodology for data-efficient discovery of dynamical systems, with broad applicability to problems where high-fidelity data acquisition is prohibitively expensive.