Newton Informed Neural Operator for Computing Multiple Solutions of Nonlinear Partials Differential Equations

Solving nonlinear partial differential equations (PDEs) with multiple solutions using neural networks has found widespread applications in various fields such as physics, biology, and engineering. However, classical neural network methods for solving nonlinear PDEs, such as Physics-Informed Neural Networks (PINN), Deep Ritz methods, and DeepONet, often encounter challenges when confronted with the presence of multiple solutions inherent in the nonlinear problem. These methods may encounter ill-posedness issues. In this paper, we propose a novel approach called the Newton Informed Neural Operator, which builds upon existing neural network techniques to tackle nonlinearities. Our method combines classical Newton methods, addressing well-posed problems, and efficiently learns multiple solutions in a single learning process while requiring fewer supervised data points compared to existing neural network methods.

Automatic Differentiation is Essential in Training Neural Networks for Solving Differential Equations

Neural network-based approaches have recently shown significant promise in solving partial differential equations (PDEs) in science and engineering, especially in scenarios featuring complex domains or the incorporation of empirical data. One advantage of the neural network method for PDEs lies in its automatic differentiation (AD), which necessitates only the sample points themselves, unlike traditional finite difference (FD) approximations that require nearby local points to compute derivatives. In this paper, we quantitatively demonstrate the advantage of AD in training neural networks. The concept of truncated entropy is introduced to characterize the training property. Specifically, through comprehensive experimental and theoretical analyses conducted on random feature models and two-layer neural networks, we discover that the defined truncated entropy serves as a reliable metric for quantifying the residual loss of random feature models and the training speed of neural networks for both AD and FD methods. Our experimental and theoretical analyses demonstrate that, from a training perspective, AD outperforms FD in solving partial differential equations.

Homotopy Relaxation Training Algorithms for Infinite-Width Two-Layer ReLU Neural Networks

In this paper, we present a novel training approach called the Homotopy Relaxation Training Algorithm (HRTA), aimed at accelerating the training process in contrast to traditional methods. Our algorithm incorporates two key mechanisms: one involves building a homotopy activation function that seamlessly connects the linear activation function with the ReLU activation function; the other technique entails relaxing the homotopy parameter to enhance the training refinement process. We have conducted an in-depth analysis of this novel method within the context of the neural tangent kernel (NTK), revealing significantly improved convergence rates. Our experimental results, especially when considering networks with larger widths, validate the theoretical conclusions. This proposed HRTA exhibits the potential for other activation functions and deep neural networks.

HomPINNs: homotopy physics-informed neural networks for solving the inverse problems of nonlinear differential equations with multiple solutions

Due to the complex behavior arising from non-uniqueness, symmetry, and bifurcations in the solution space, solving inverse problems of nonlinear differential equations (DEs) with multiple solutions is a challenging task. To address this issue, we propose homotopy physics-informed neural networks (HomPINNs), a novel framework that leverages homotopy continuation and neural networks (NNs) to solve inverse problems. The proposed framework begins with the use of a NN to simultaneously approximate known observations and conform to the constraints of DEs. By utilizing the homotopy continuation method, the approximation traces the observations to identify multiple solutions and solve the inverse problem. The experiments involve testing the performance of the proposed method on one-dimensional DEs and applying it to solve a two-dimensional Gray-Scott simulation. Our findings demonstrate that the proposed method is scalable and adaptable, providing an effective solution for solving DEs with multiple solutions and unknown parameters. Moreover, it has significant potential for various applications in scientific computing, such as modeling complex systems and solving inverse problems in physics, chemistry, biology, etc.

Stability Preserving Data-driven Models With Latent Dynamics

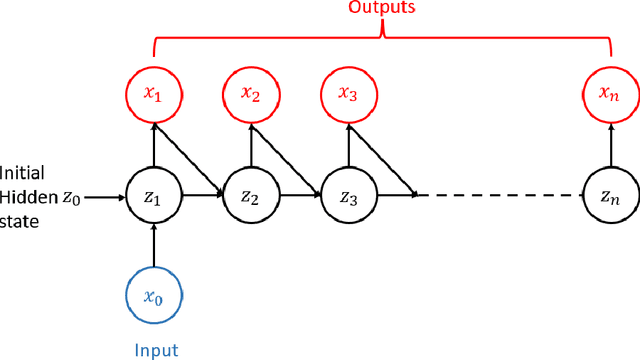
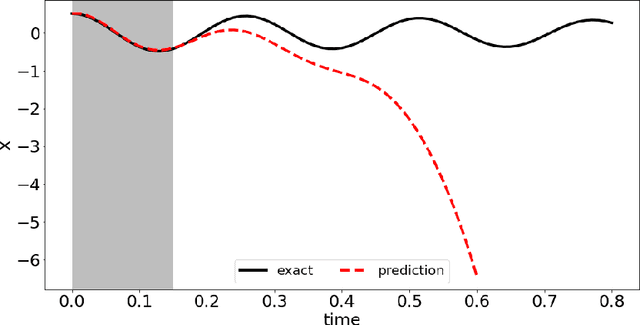
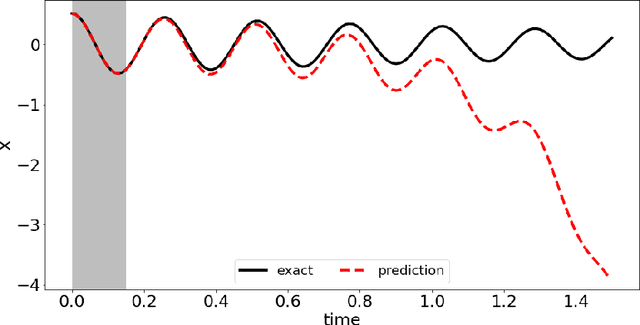
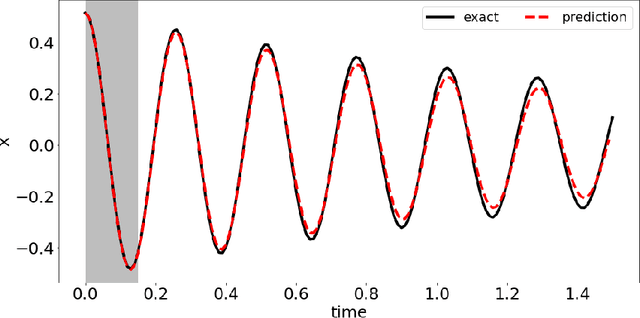
In this paper, we introduce a data-driven modeling approach for dynamics problems with latent variables. The state-space of the proposed model includes artificial latent variables, in addition to observed variables that can be fitted to a given data set. We present a model framework where the stability of the coupled dynamics can be easily enforced. The model is implemented by recurrent cells and trained using backpropagation through time. Numerical examples using benchmark tests from order reduction problems demonstrate the stability of the model and the efficiency of the recurrent cell implementation. As applications, two fluid-structure interaction problems are considered to illustrate the accuracy and predictive capability of the model.

A Weight Initialization Based on the Linear Product Structure for Neural Networks

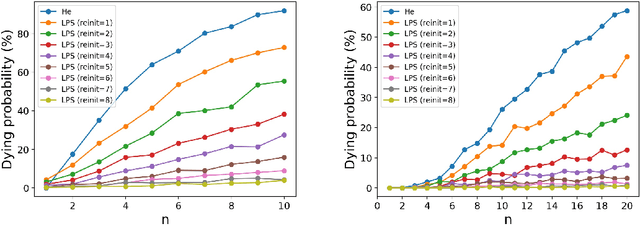
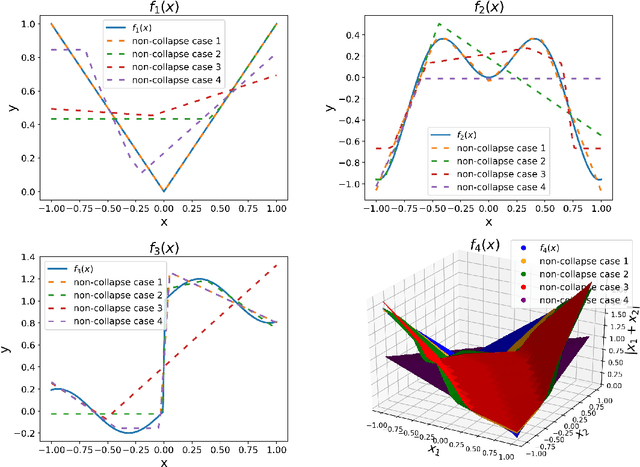
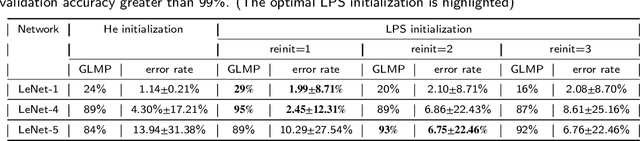
Weight initialization plays an important role in training neural networks and also affects tremendous deep learning applications. Various weight initialization strategies have already been developed for different activation functions with different neural networks. These initialization algorithms are based on minimizing the variance of the parameters between layers and might still fail when neural networks are deep, e.g., dying ReLU. To address this challenge, we study neural networks from a nonlinear computation point of view and propose a novel weight initialization strategy that is based on the linear product structure (LPS) of neural networks. The proposed strategy is derived from the polynomial approximation of activation functions by using theories of numerical algebraic geometry to guarantee to find all the local minima. We also provide a theoretical analysis that the LPS initialization has a lower probability of dying ReLU comparing to other existing initialization strategies. Finally, we test the LPS initialization algorithm on both fully connected neural networks and convolutional neural networks to show its feasibility, efficiency, and robustness on public datasets.

A machine learning method correlating pulse pressure wave data with pregnancy

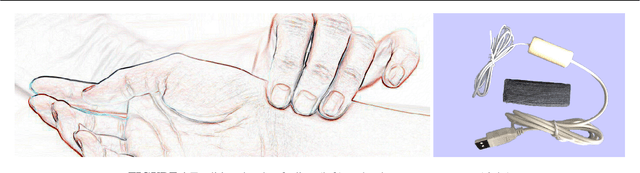
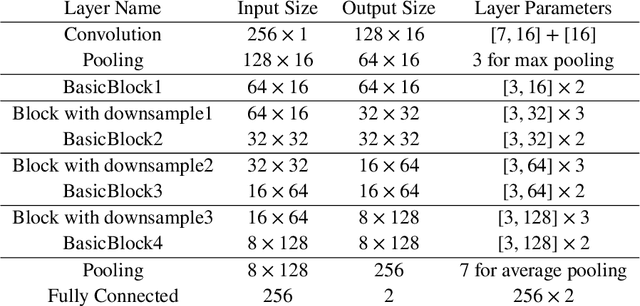
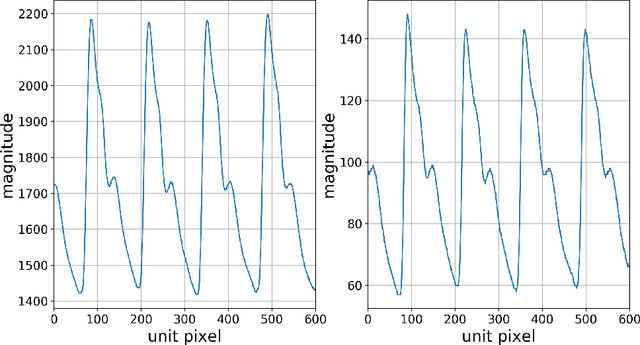
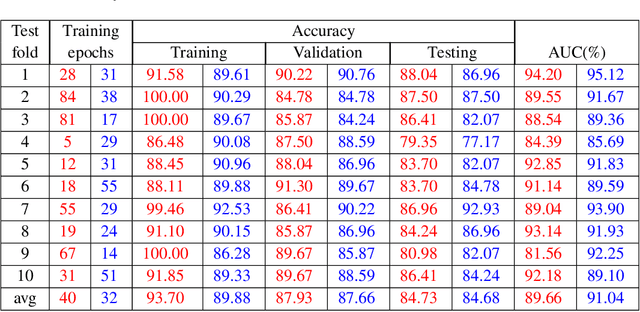
Pulse feeling, representing the tactile arterial palpation of the heartbeat, has been widely used in traditional Chinese medicine (TCM) to diagnose various diseases. The quantitative relationship between the pulse wave and health conditions however has not been investigated in modern medicine. In this paper, we explored the correlation between pulse pressure wave (PPW), rather than the pulse key features in TCM, and pregnancy by using deep learning technology. This computational approach shows that the accuracy of pregnancy detection by the PPW is 84% with an AUC of 91%. Our study is a proof of concept of pulse diagnosis and will also motivate further sophisticated investigations on pulse waves.