Policy Gradient with Tree Search: Avoiding Local Optimas through Lookahead

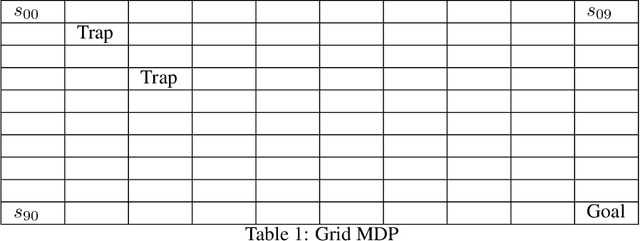
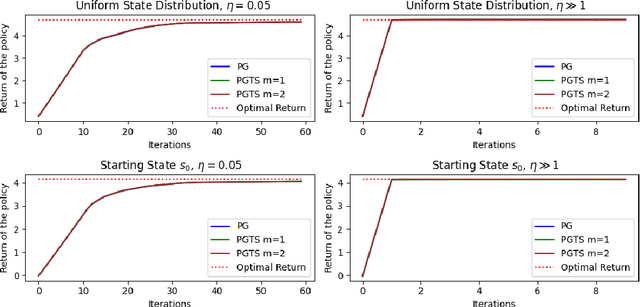
Classical policy gradient (PG) methods in reinforcement learning frequently converge to suboptimal local optima, a challenge exacerbated in large or complex environments. This work investigates Policy Gradient with Tree Search (PGTS), an approach that integrates an $m$-step lookahead mechanism to enhance policy optimization. We provide theoretical analysis demonstrating that increasing the tree search depth $m$-monotonically reduces the set of undesirable stationary points and, consequently, improves the worst-case performance of any resulting stationary policy. Critically, our analysis accommodates practical scenarios where policy updates are restricted to states visited by the current policy, rather than requiring updates across the entire state space. Empirical evaluations on diverse MDP structures, including Ladder, Tightrope, and Gridworld environments, illustrate PGTS's ability to exhibit "farsightedness," navigate challenging reward landscapes, escape local traps where standard PG fails, and achieve superior solutions.

Learning Equilibria from Data: Provably Efficient Multi-Agent Imitation Learning

This paper provides the first expert sample complexity characterization for learning a Nash equilibrium from expert data in Markov Games. We show that a new quantity named the single policy deviation concentrability coefficient is unavoidable in the non-interactive imitation learning setting, and we provide an upper bound for behavioral cloning (BC) featuring such coefficient. BC exhibits substantial regret in games with high concentrability coefficient, leading us to utilize expert queries to develop and introduce two novel solution algorithms: MAIL-BRO and MURMAIL. The former employs a best response oracle and learns an $\varepsilon$-Nash equilibrium with $\mathcal{O}(\varepsilon^{-4})$ expert and oracle queries. The latter bypasses completely the best response oracle at the cost of a worse expert query complexity of order $\mathcal{O}(\varepsilon^{-8})$. Finally, we provide numerical evidence, confirming our theoretical findings.

Clustered KL-barycenter design for policy evaluation

In the context of stochastic bandit models, this article examines how to design sample-efficient behavior policies for the importance sampling evaluation of multiple target policies. From importance sampling theory, it is well established that sample efficiency is highly sensitive to the KL divergence between the target and importance sampling distributions. We first analyze a single behavior policy defined as the KL-barycenter of the target policies. Then, we refine this approach by clustering the target policies into groups with small KL divergences and assigning each cluster its own KL-barycenter as a behavior policy. This clustered KL-based policy evaluation (CKL-PE) algorithm provides a novel perspective on optimal policy selection. We prove upper bounds on the sample complexity of our method and demonstrate its effectiveness with numerical validation.

Dual Formulation for Non-Rectangular Lp Robust Markov Decision Processes

We study robust Markov decision processes (RMDPs) with non-rectangular uncertainty sets, which capture interdependencies across states unlike traditional rectangular models. While non-rectangular robust policy evaluation is generally NP-hard, even in approximation, we identify a powerful class of $L_p$-bounded uncertainty sets that avoid these complexity barriers due to their structural simplicity. We further show that this class can be decomposed into infinitely many \texttt{sa}-rectangular $L_p$-bounded sets and leverage its structural properties to derive a novel dual formulation for $L_p$ RMDPs. This formulation provides key insights into the adversary's strategy and enables the development of the first robust policy evaluation algorithms for non-rectangular RMDPs. Empirical results demonstrate that our approach significantly outperforms brute-force methods, establishing a promising foundation for future investigation into non-rectangular robust MDPs.

On Multi-Agent Inverse Reinforcement Learning

In multi-agent systems, the agent behavior is highly influenced by its utility function, as these utilities shape both individual goals as well as interactions with the other agents. Inverse Reinforcement Learning (IRL) is a well-established approach to inferring the utility function by observing an expert behavior within a given environment. In this paper, we extend the IRL framework to the multi-agent setting, assuming to observe agents who are following Nash Equilibrium (NE) policies. We theoretically investigate the set of utilities that explain the behavior of NE experts. Specifically, we provide an explicit characterization of the feasible reward set and analyze how errors in estimating the transition dynamics and expert behavior impact the recovered rewards. Building on these findings, we provide the first sample complexity analysis for the multi-agent IRL problem. Finally, we provide a numerical evaluation of our theoretical results.

Improved Sample Complexity for Global Convergence of Actor-Critic Algorithms

In this paper, we establish the global convergence of the actor-critic algorithm with a significantly improved sample complexity of $O(\epsilon^{-3})$, advancing beyond the existing local convergence results. Previous works provide local convergence guarantees with a sample complexity of $O(\epsilon^{-2})$ for bounding the squared gradient of the return, which translates to a global sample complexity of $O(\epsilon^{-4})$ using the gradient domination lemma. In contrast to traditional methods that employ decreasing step sizes for both the actor and critic, we demonstrate that a constant step size for the critic is sufficient to ensure convergence in expectation. This key insight reveals that using a decreasing step size for the actor alone is sufficient to handle the noise for both the actor and critic. Our findings provide theoretical support for the practical success of many algorithms that rely on constant step sizes.

Preference Elicitation for Offline Reinforcement Learning

Applying reinforcement learning (RL) to real-world problems is often made challenging by the inability to interact with the environment and the difficulty of designing reward functions. Offline RL addresses the first challenge by considering access to an offline dataset of environment interactions labeled by the reward function. In contrast, Preference-based RL does not assume access to the reward function and learns it from preferences, but typically requires an online interaction with the environment. We bridge the gap between these frameworks by exploring efficient methods for acquiring preference feedback in a fully offline setup. We propose Sim-OPRL, an offline preference-based reinforcement learning algorithm, which leverages a learned environment model to elicit preference feedback on simulated rollouts. Drawing on insights from both the offline RL and the preference-based RL literature, our algorithm employs a pessimistic approach for out-of-distribution data, and an optimistic approach for acquiring informative preferences about the optimal policy. We provide theoretical guarantees regarding the sample complexity of our approach, dependent on how well the offline data covers the optimal policy. Finally, we demonstrate the empirical performance of Sim-OPRL in different environments.

Stochastic Bilevel Optimization with Lower-Level Contextual Markov Decision Processes

In various applications, the optimal policy in a strategic decision-making problem depends both on the environmental configuration and exogenous events. For these settings, we introduce Bilevel Optimization with Contextual Markov Decision Processes (BO-CMDP), a stochastic bilevel decision-making model, where the lower level consists of solving a contextual Markov Decision Process (CMDP). BO-CMDP can be viewed as a Stackelberg Game where the leader and a random context beyond the leader's control together decide the setup of (many) MDPs that (potentially multiple) followers best respond to. This framework extends beyond traditional bilevel optimization and finds relevance in diverse fields such as model design for MDPs, tax design, reward shaping and dynamic mechanism design. We propose a stochastic Hyper Policy Gradient Descent (HPGD) algorithm to solve BO-CMDP, and demonstrate its convergence. Notably, HPGD only utilizes observations of the followers' trajectories. Therefore, it allows followers to use any training procedure and the leader to be agnostic of the specific algorithm used, which aligns with various real-world scenarios. We further consider the setting when the leader can influence the training of followers and propose an accelerated algorithm. We empirically demonstrate the performance of our algorithm.

Truly No-Regret Learning in Constrained MDPs

Constrained Markov decision processes (CMDPs) are a common way to model safety constraints in reinforcement learning. State-of-the-art methods for efficiently solving CMDPs are based on primal-dual algorithms. For these algorithms, all currently known regret bounds allow for error cancellations -- one can compensate for a constraint violation in one round with a strict constraint satisfaction in another. This makes the online learning process unsafe since it only guarantees safety for the final (mixture) policy but not during learning. As Efroni et al. (2020) pointed out, it is an open question whether primal-dual algorithms can provably achieve sublinear regret if we do not allow error cancellations. In this paper, we give the first affirmative answer. We first generalize a result on last-iterate convergence of regularized primal-dual schemes to CMDPs with multiple constraints. Building upon this insight, we propose a model-based primal-dual algorithm to learn in an unknown CMDP. We prove that our algorithm achieves sublinear regret without error cancellations.

Exploiting Causal Graph Priors with Posterior Sampling for Reinforcement Learning

Posterior sampling allows the exploitation of prior knowledge of the environment's transition dynamics to improve the sample efficiency of reinforcement learning. The prior is typically specified as a class of parametric distributions, a task that can be cumbersome in practice, often resulting in the choice of uninformative priors. In this work, we propose a novel posterior sampling approach in which the prior is given as a (partial) causal graph over the environment's variables. The latter is often more natural to design, such as listing known causal dependencies between biometric features in a medical treatment study. Specifically, we propose a hierarchical Bayesian procedure, called C-PSRL, simultaneously learning the full causal graph at the higher level and the parameters of the resulting factored dynamics at the lower level. For this procedure, we provide an analysis of its Bayesian regret, which explicitly connects the regret rate with the degree of prior knowledge. Our numerical evaluation conducted in illustrative domains confirms that C-PSRL strongly improves the efficiency of posterior sampling with an uninformative prior while performing close to posterior sampling with the full causal graph.