Inverse Q-Learning Done Right: Offline Imitation Learning in $Q^π$-Realizable MDPs

We study the problem of offline imitation learning in Markov decision processes (MDPs), where the goal is to learn a well-performing policy given a dataset of state-action pairs generated by an expert policy. Complementing a recent line of work on this topic that assumes the expert belongs to a tractable class of known policies, we approach this problem from a new angle and leverage a different type of structural assumption about the environment. Specifically, for the class of linear $Q^\pi$-realizable MDPs, we introduce a new algorithm called saddle-point offline imitation learning (\SPOIL), which is guaranteed to match the performance of any expert up to an additive error $\varepsilon$ with access to $\mathcal{O}(\varepsilon^{-2})$ samples. Moreover, we extend this result to possibly non-linear $Q^\pi$-realizable MDPs at the cost of a worse sample complexity of order $\mathcal{O}(\varepsilon^{-4})$. Finally, our analysis suggests a new loss function for training critic networks from expert data in deep imitation learning. Empirical evaluations on standard benchmarks demonstrate that the neural net implementation of \SPOIL is superior to behavior cloning and competitive with state-of-the-art algorithms.

Learning Equilibria from Data: Provably Efficient Multi-Agent Imitation Learning

This paper provides the first expert sample complexity characterization for learning a Nash equilibrium from expert data in Markov Games. We show that a new quantity named the single policy deviation concentrability coefficient is unavoidable in the non-interactive imitation learning setting, and we provide an upper bound for behavioral cloning (BC) featuring such coefficient. BC exhibits substantial regret in games with high concentrability coefficient, leading us to utilize expert queries to develop and introduce two novel solution algorithms: MAIL-BRO and MURMAIL. The former employs a best response oracle and learns an $\varepsilon$-Nash equilibrium with $\mathcal{O}(\varepsilon^{-4})$ expert and oracle queries. The latter bypasses completely the best response oracle at the cost of a worse expert query complexity of order $\mathcal{O}(\varepsilon^{-8})$. Finally, we provide numerical evidence, confirming our theoretical findings.

IL-SOAR : Imitation Learning with Soft Optimistic Actor cRitic

This paper introduces the SOAR framework for imitation learning. SOAR is an algorithmic template that learns a policy from expert demonstrations with a primal dual style algorithm that alternates cost and policy updates. Within the policy updates, the SOAR framework uses an actor critic method with multiple critics to estimate the critic uncertainty and build an optimistic critic fundamental to drive exploration. When instantiated in the tabular setting, we get a provable algorithm with guarantees that matches the best known results in $\epsilon$. Practically, the SOAR template is shown to boost consistently the performance of imitation learning algorithms based on Soft Actor Critic such as f-IRL, ML-IRL and CSIL in several MuJoCo environments. Overall, thanks to SOAR, the required number of episodes to achieve the same performance is reduced by half.

Optimistically Optimistic Exploration for Provably Efficient Infinite-Horizon Reinforcement and Imitation Learning

We study the problem of reinforcement learning in infinite-horizon discounted linear Markov decision processes (MDPs), and propose the first computationally efficient algorithm achieving near-optimal regret guarantees in this setting. Our main idea is to combine two classic techniques for optimistic exploration: additive exploration bonuses applied to the reward function, and artificial transitions made to an absorbing state with maximal return. We show that, combined with a regularized approximate dynamic-programming scheme, the resulting algorithm achieves a regret of order $\tilde{\mathcal{O}} (\sqrt{d^3 (1 - \gamma)^{- 7 / 2} T})$, where $T$ is the total number of sample transitions, $\gamma \in (0,1)$ is the discount factor, and $d$ is the feature dimensionality. The results continue to hold against adversarial reward sequences, enabling application of our method to the problem of imitation learning in linear MDPs, where we achieve state-of-the-art results.

Multi-Step Alignment as Markov Games: An Optimistic Online Gradient Descent Approach with Convergence Guarantees

Reinforcement Learning from Human Feedback (RLHF) has been highly successful in aligning large language models with human preferences. While prevalent methods like DPO have demonstrated strong performance, they frame interactions with the language model as a bandit problem, which limits their applicability in real-world scenarios where multi-turn conversations are common. Additionally, DPO relies on the Bradley-Terry model assumption, which does not adequately capture the non-transitive nature of human preferences. In this paper, we address these challenges by modeling the alignment problem as a two-player constant-sum Markov game, where each player seeks to maximize their winning rate against the other across all steps of the conversation. Our approach Multi-step Preference Optimization (MPO) is built upon the natural actor-critic framework~\citep{peters2008natural}. We further develop OMPO based on the optimistic online gradient descent algorithm~\citep{rakhlin2013online,joulani17a}. Theoretically, we provide a rigorous analysis for both algorithms on convergence and show that OMPO requires $\mathcal{O}(\epsilon^{-1})$ policy updates to converge to an $\epsilon$-approximate Nash equilibrium. We also validate the effectiveness of our method on multi-turn conversations dataset and math reasoning dataset.

Best of Both Worlds: Regret Minimization versus Minimax Play

In this paper, we investigate the existence of online learning algorithms with bandit feedback that simultaneously guarantee $O(1)$ regret compared to a given comparator strategy, and $O(\sqrt{T})$ regret compared to the best strategy in hindsight, where $T$ is the number of rounds. We provide the first affirmative answer to this question. In the context of symmetric zero-sum games, both in normal- and extensive form, we show that our results allow us to guarantee to risk at most $O(1)$ loss while being able to gain $\Omega(T)$ from exploitable opponents, thereby combining the benefits of both no-regret algorithms and minimax play.

Imitation Learning in Discounted Linear MDPs without exploration assumptions

We present a new algorithm for imitation learning in infinite horizon linear MDPs dubbed ILARL which greatly improves the bound on the number of trajectories that the learner needs to sample from the environment. In particular, we remove exploration assumptions required in previous works and we improve the dependence on the desired accuracy $\epsilon$ from $\mathcal{O}\br{\epsilon^{-5}}$ to $\mathcal{O}\br{\epsilon^{-4}}$. Our result relies on a connection between imitation learning and online learning in MDPs with adversarial losses. For the latter setting, we present the first result for infinite horizon linear MDP which may be of independent interest. Moreover, we are able to provide a strengthen result for the finite horizon case where we achieve $\mathcal{O}\br{\epsilon^{-2}}$. Numerical experiments with linear function approximation shows that ILARL outperforms other commonly used algorithms.

Provable benefits of general coverage conditions in efficient online RL with function approximation

In online reinforcement learning (RL), instead of employing standard structural assumptions on Markov decision processes (MDPs), using a certain coverage condition (original from offline RL) is enough to ensure sample-efficient guarantees (Xie et al. 2023). In this work, we focus on this new direction by digging more possible and general coverage conditions, and study the potential and the utility of them in efficient online RL. We identify more concepts, including the $L^p$ variant of concentrability, the density ratio realizability, and trade-off on the partial/rest coverage condition, that can be also beneficial to sample-efficient online RL, achieving improved regret bound. Furthermore, if exploratory offline data are used, under our coverage conditions, both statistically and computationally efficient guarantees can be achieved for online RL. Besides, even though the MDP structure is given, e.g., linear MDP, we elucidate that, good coverage conditions are still beneficial to obtain faster regret bound beyond $\widetilde{O}(\sqrt{T})$ and even a logarithmic order regret. These results provide a good justification for the usage of general coverage conditions in efficient online RL.

Identifiability and generalizability from multiple experts in Inverse Reinforcement Learning

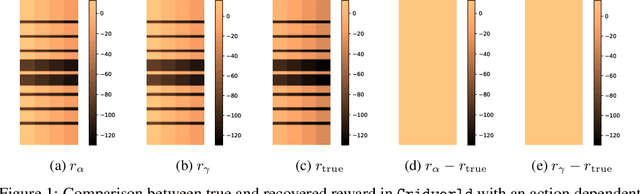
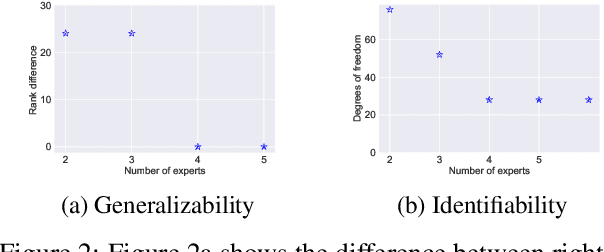
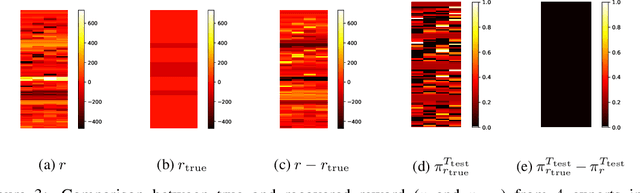
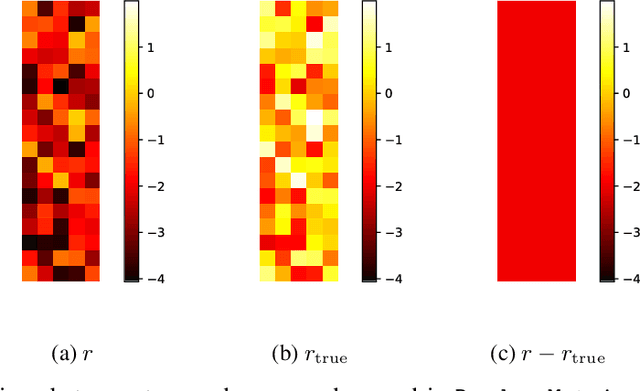
While Reinforcement Learning (RL) aims to train an agent from a reward function in a given environment, Inverse Reinforcement Learning (IRL) seeks to recover the reward function from observing an expert's behavior. It is well known that, in general, various reward functions can lead to the same optimal policy, and hence, IRL is ill-defined. However, (Cao et al., 2021) showed that, if we observe two or more experts with different discount factors or acting in different environments, the reward function can under certain conditions be identified up to a constant. This work starts by showing an equivalent identifiability statement from multiple experts in tabular MDPs based on a rank condition, which is easily verifiable and is shown to be also necessary. We then extend our result to various different scenarios, i.e., we characterize reward identifiability in the case where the reward function can be represented as a linear combination of given features, making it more interpretable, or when we have access to approximate transition matrices. Even when the reward is not identifiable, we provide conditions characterizing when data on multiple experts in a given environment allows to generalize and train an optimal agent in a new environment. Our theoretical results on reward identifiability and generalizability are validated in various numerical experiments.

Proximal Point Imitation Learning

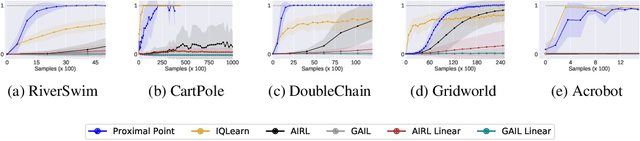
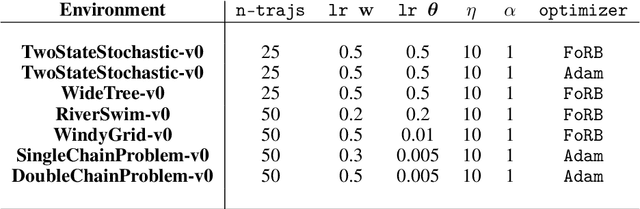
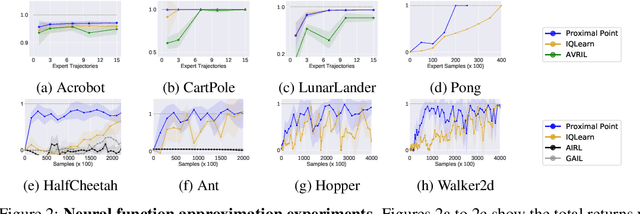
This work develops new algorithms with rigorous efficiency guarantees for infinite horizon imitation learning (IL) with linear function approximation without restrictive coherence assumptions. We begin with the minimax formulation of the problem and then outline how to leverage classical tools from optimization, in particular, the proximal-point method (PPM) and dual smoothing, for online and offline IL, respectively. Thanks to PPM, we avoid nested policy evaluation and cost updates for online IL appearing in the prior literature. In particular, we do away with the conventional alternating updates by the optimization of a single convex and smooth objective over both cost and Q-functions. When solved inexactly, we relate the optimization errors to the suboptimality of the recovered policy. As an added bonus, by re-interpreting PPM as dual smoothing with the expert policy as a center point, we also obtain an offline IL algorithm enjoying theoretical guarantees in terms of required expert trajectories. Finally, we achieve convincing empirical performance for both linear and neural network function approximation.