Policy Gradient with Tree Search: Avoiding Local Optimas through Lookahead
Paper and Code
Jun 08, 2025
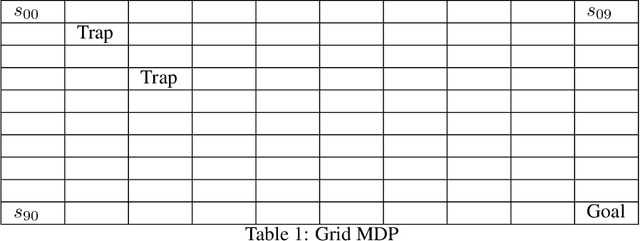
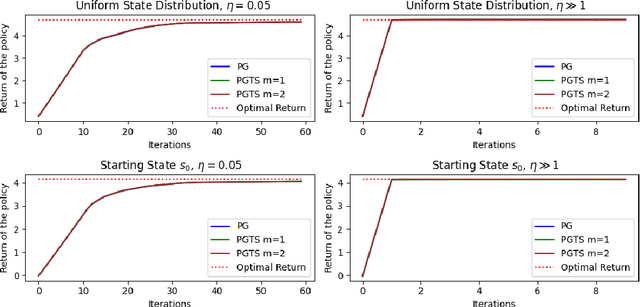

Classical policy gradient (PG) methods in reinforcement learning frequently converge to suboptimal local optima, a challenge exacerbated in large or complex environments. This work investigates Policy Gradient with Tree Search (PGTS), an approach that integrates an $m$-step lookahead mechanism to enhance policy optimization. We provide theoretical analysis demonstrating that increasing the tree search depth $m$-monotonically reduces the set of undesirable stationary points and, consequently, improves the worst-case performance of any resulting stationary policy. Critically, our analysis accommodates practical scenarios where policy updates are restricted to states visited by the current policy, rather than requiring updates across the entire state space. Empirical evaluations on diverse MDP structures, including Ladder, Tightrope, and Gridworld environments, illustrate PGTS's ability to exhibit "farsightedness," navigate challenging reward landscapes, escape local traps where standard PG fails, and achieve superior solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge