Global Solutions to Non-Convex Functional Constrained Problems with Hidden Convexity

Constrained non-convex optimization is fundamentally challenging, as global solutions are generally intractable and constraint qualifications may not hold. However, in many applications, including safe policy optimization in control and reinforcement learning, such problems possess hidden convexity, meaning they can be reformulated as convex programs via a nonlinear invertible transformation. Typically such transformations are implicit or unknown, making the direct link with the convex program impossible. On the other hand, (sub-)gradients with respect to the original variables are often accessible or can be easily estimated, which motivates algorithms that operate directly in the original (non-convex) problem space using standard (sub-)gradient oracles. In this work, we develop the first algorithms to provably solve such non-convex problems to global minima. First, using a modified inexact proximal point method, we establish global last-iterate convergence guarantees with $\widetilde{\mathcal{O}}(\varepsilon^{-3})$ oracle complexity in non-smooth setting. For smooth problems, we propose a new bundle-level type method based on linearly constrained quadratic subproblems, improving the oracle complexity to $\widetilde{\mathcal{O}}(\varepsilon^{-1})$. Surprisingly, despite non-convexity, our methodology does not require any constraint qualifications, can handle hidden convex equality constraints, and achieves complexities matching those for solving unconstrained hidden convex optimization.

Scalable Neural Incentive Design with Parameterized Mean-Field Approximation

Designing incentives for a multi-agent system to induce a desirable Nash equilibrium is both a crucial and challenging problem appearing in many decision-making domains, especially for a large number of agents $N$. Under the exchangeability assumption, we formalize this incentive design (ID) problem as a parameterized mean-field game (PMFG), aiming to reduce complexity via an infinite-population limit. We first show that when dynamics and rewards are Lipschitz, the finite-$N$ ID objective is approximated by the PMFG at rate $\mathscr{O}(\frac{1}{\sqrt{N}})$. Moreover, beyond the Lipschitz-continuous setting, we prove the same $\mathscr{O}(\frac{1}{\sqrt{N}})$ decay for the important special case of sequential auctions, despite discontinuities in dynamics, through a tailored auction-specific analysis. Built on our novel approximation results, we further introduce our Adjoint Mean-Field Incentive Design (AMID) algorithm, which uses explicit differentiation of iterated equilibrium operators to compute gradients efficiently. By uniting approximation bounds with optimization guarantees, AMID delivers a powerful, scalable algorithmic tool for many-agent (large $N$) ID. Across diverse auction settings, the proposed AMID method substantially increases revenue over first-price formats and outperforms existing benchmark methods.

Natural Gradient VI: Guarantees for Non-Conjugate Models

Stochastic Natural Gradient Variational Inference (NGVI) is a widely used method for approximating posterior distribution in probabilistic models. Despite its empirical success and foundational role in variational inference, its theoretical underpinnings remain limited, particularly in the case of non-conjugate likelihoods. While NGVI has been shown to be a special instance of Stochastic Mirror Descent, and recent work has provided convergence guarantees using relative smoothness and strong convexity for conjugate models, these results do not extend to the non-conjugate setting, where the variational loss becomes non-convex and harder to analyze. In this work, we focus on mean-field parameterization and advance the theoretical understanding of NGVI in three key directions. First, we derive sufficient conditions under which the variational loss satisfies relative smoothness with respect to a suitable mirror map. Second, leveraging this structure, we propose a modified NGVI algorithm incorporating non-Euclidean projections and prove its global non-asymptotic convergence to a stationary point. Finally, under additional structural assumptions about the likelihood, we uncover hidden convexity properties of the variational loss and establish fast global convergence of NGVI to a global optimum. These results provide new insights into the geometry and convergence behavior of NGVI in challenging inference settings.

Provable Maximum Entropy Manifold Exploration via Diffusion Models

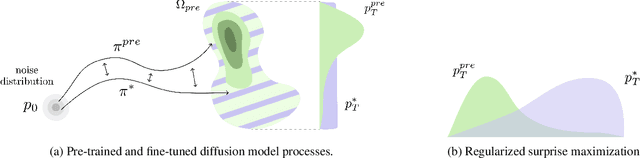
Exploration is critical for solving real-world decision-making problems such as scientific discovery, where the objective is to generate truly novel designs rather than mimic existing data distributions. In this work, we address the challenge of leveraging the representational power of generative models for exploration without relying on explicit uncertainty quantification. We introduce a novel framework that casts exploration as entropy maximization over the approximate data manifold implicitly defined by a pre-trained diffusion model. Then, we present a novel principle for exploration based on density estimation, a problem well-known to be challenging in practice. To overcome this issue and render this method truly scalable, we leverage a fundamental connection between the entropy of the density induced by a diffusion model and its score function. Building on this, we develop an algorithm based on mirror descent that solves the exploration problem as sequential fine-tuning of a pre-trained diffusion model. We prove its convergence to the optimal exploratory diffusion model under realistic assumptions by leveraging recent understanding of mirror flows. Finally, we empirically evaluate our approach on both synthetic and high-dimensional text-to-image diffusion, demonstrating promising results.

Zeroth-Order Optimization Finds Flat Minima

Zeroth-order methods are extensively used in machine learning applications where gradients are infeasible or expensive to compute, such as black-box attacks, reinforcement learning, and language model fine-tuning. Existing optimization theory focuses on convergence to an arbitrary stationary point, but less is known on the implicit regularization that provides a fine-grained characterization on which particular solutions are finally reached. We show that zeroth-order optimization with the standard two-point estimator favors solutions with small trace of Hessian, which is widely used in previous work to distinguish between sharp and flat minima. We further provide convergence rates of zeroth-order optimization to approximate flat minima for convex and sufficiently smooth functions, where flat minima are defined as the minimizers that achieve the smallest trace of Hessian among all optimal solutions. Experiments on binary classification tasks with convex losses and language model fine-tuning support our theoretical findings.

AmorLIP: Efficient Language-Image Pretraining via Amortization

Contrastive Language-Image Pretraining (CLIP) has demonstrated strong zero-shot performance across diverse downstream text-image tasks. Existing CLIP methods typically optimize a contrastive objective using negative samples drawn from each minibatch. To achieve robust representation learning, these methods require extremely large batch sizes and escalate computational demands to hundreds or even thousands of GPUs. Prior approaches to mitigate this issue often compromise downstream performance, prolong training duration, or face scalability challenges with very large datasets. To overcome these limitations, we propose AmorLIP, an efficient CLIP pretraining framework that amortizes expensive computations involved in contrastive learning through lightweight neural networks, which substantially improves training efficiency and performance. Leveraging insights from a spectral factorization of energy-based models, we introduce novel amortization objectives along with practical techniques to improve training stability. Extensive experiments across 38 downstream tasks demonstrate the superior zero-shot classification and retrieval capabilities of AmorLIP, consistently outperforming standard CLIP baselines with substantial relative improvements of up to 12.24%.

Steering No-Regret Agents in MFGs under Model Uncertainty

Incentive design is a popular framework for guiding agents' learning dynamics towards desired outcomes by providing additional payments beyond intrinsic rewards. However, most existing works focus on a finite, small set of agents or assume complete knowledge of the game, limiting their applicability to real-world scenarios involving large populations and model uncertainty. To address this gap, we study the design of steering rewards in Mean-Field Games (MFGs) with density-independent transitions, where both the transition dynamics and intrinsic reward functions are unknown. This setting presents non-trivial challenges, as the mediator must incentivize the agents to explore for its model learning under uncertainty, while simultaneously steer them to converge to desired behaviors without incurring excessive incentive payments. Assuming agents exhibit no(-adaptive) regret behaviors, we contribute novel optimistic exploration algorithms. Theoretically, we establish sub-linear regret guarantees for the cumulative gaps between the agents' behaviors and the desired ones. In terms of the steering cost, we demonstrate that our total incentive payments incur only sub-linear excess, competing with a baseline steering strategy that stabilizes the target policy as an equilibrium. Our work presents an effective framework for steering agents behaviors in large-population systems under uncertainty.

Can RLHF be More Efficient with Imperfect Reward Models? A Policy Coverage Perspective

Sample efficiency is critical for online Reinforcement Learning from Human Feedback (RLHF). While existing works investigate sample-efficient online exploration strategies, the potential of utilizing misspecified yet relevant reward models to accelerate learning remains underexplored. This paper studies how to transfer knowledge from those imperfect reward models in online RLHF. We start by identifying a novel property of the KL-regularized RLHF objective: \emph{a policy's ability to cover the optimal policy is captured by its sub-optimality}. Building on this insight, we propose a theoretical transfer learning algorithm with provable benefits compared to standard online learning. Our approach achieves low regret in the early stage by quickly adapting to the best available source reward models without prior knowledge of their quality, and over time, it attains an $\tilde{O}(\sqrt{T})$ regret bound \emph{independent} of structural complexity measures. Inspired by our theoretical findings, we develop an empirical algorithm with improved computational efficiency, and demonstrate its effectiveness empirically in summarization tasks.

Poincaré Inequality for Local Log-Polyak-Lojasiewicz Measures : Non-asymptotic Analysis in Low-temperature Regime

Potential functions in highly pertinent applications, such as deep learning in over-parameterized regime, are empirically observed to admit non-isolated minima. To understand the convergence behavior of stochastic dynamics in such landscapes, we propose to study the class of \logPLmeasure\ measures $\mu_\epsilon \propto \exp(-V/\epsilon)$, where the potential $V$ satisfies a local Polyak-{\L}ojasiewicz (P\L) inequality, and its set of local minima is provably \emph{connected}. Notably, potentials in this class can exhibit local maxima and we characterize its optimal set S to be a compact $\mathcal{C}^2$ \emph{embedding submanifold} of $\mathbb{R}^d$ without boundary. The \emph{non-contractibility} of S distinguishes our function class from the classical convex setting topologically. Moreover, the embedding structure induces a naturally defined Laplacian-Beltrami operator on S, and we show that its first non-trivial eigenvalue provides an \emph{$\epsilon$-independent} lower bound for the \Poincare\ constant in the \Poincare\ inequality of $\mu_\epsilon$. As a direct consequence, Langevin dynamics with such non-convex potential $V$ and diffusion coefficient $\epsilon$ converges to its equilibrium $\mu_\epsilon$ at a rate of $\tilde{\mathcal{O}}(1/\epsilon)$, provided $\epsilon$ is sufficiently small. Here $\tilde{\mathcal{O}}$ hides logarithmic terms.

On the Crucial Role of Initialization for Matrix Factorization

This work revisits the classical low-rank matrix factorization problem and unveils the critical role of initialization in shaping convergence rates for such nonconvex and nonsmooth optimization. We introduce Nystrom initialization, which significantly improves the global convergence of Scaled Gradient Descent (ScaledGD) in both symmetric and asymmetric matrix factorization tasks. Specifically, we prove that ScaledGD with Nystrom initialization achieves quadratic convergence in cases where only linear rates were previously known. Furthermore, we extend this initialization to low-rank adapters (LoRA) commonly used for finetuning foundation models. Our approach, NoRA, i.e., LoRA with Nystrom initialization, demonstrates superior performance across various downstream tasks and model scales, from 1B to 7B parameters, in large language and diffusion models.