Efficient Personalization of Generative Models via Optimal Experimental Design

Preference learning from human feedback has the ability to align generative models with the needs of end-users. Human feedback is costly and time-consuming to obtain, which creates demand for data-efficient query selection methods. This work presents a novel approach that leverages optimal experimental design to ask humans the most informative preference queries, from which we can elucidate the latent reward function modeling user preferences efficiently. We formulate the problem of preference query selection as the one that maximizes the information about the underlying latent preference model. We show that this problem has a convex optimization formulation, and introduce a statistically and computationally efficient algorithm ED-PBRL that is supported by theoretical guarantees and can efficiently construct structured queries such as images or text. We empirically present the proposed framework by personalizing a text-to-image generative model to user-specific styles, showing that it requires less preference queries compared to random query selection.

Provable Maximum Entropy Manifold Exploration via Diffusion Models

Exploration is critical for solving real-world decision-making problems such as scientific discovery, where the objective is to generate truly novel designs rather than mimic existing data distributions. In this work, we address the challenge of leveraging the representational power of generative models for exploration without relying on explicit uncertainty quantification. We introduce a novel framework that casts exploration as entropy maximization over the approximate data manifold implicitly defined by a pre-trained diffusion model. Then, we present a novel principle for exploration based on density estimation, a problem well-known to be challenging in practice. To overcome this issue and render this method truly scalable, we leverage a fundamental connection between the entropy of the density induced by a diffusion model and its score function. Building on this, we develop an algorithm based on mirror descent that solves the exploration problem as sequential fine-tuning of a pre-trained diffusion model. We prove its convergence to the optimal exploratory diffusion model under realistic assumptions by leveraging recent understanding of mirror flows. Finally, we empirically evaluate our approach on both synthetic and high-dimensional text-to-image diffusion, demonstrating promising results.

Geometric Active Exploration in Markov Decision Processes: the Benefit of Abstraction

How can a scientist use a Reinforcement Learning (RL) algorithm to design experiments over a dynamical system's state space? In the case of finite and Markovian systems, an area called Active Exploration (AE) relaxes the optimization problem of experiments design into Convex RL, a generalization of RL admitting a wider notion of reward. Unfortunately, this framework is currently not scalable and the potential of AE is hindered by the vastness of experiment spaces typical of scientific discovery applications. However, these spaces are often endowed with natural geometries, e.g., permutation invariance in molecular design, that an agent could leverage to improve the statistical and computational efficiency of AE. To achieve this, we bridge AE and MDP homomorphisms, which offer a way to exploit known geometric structures via abstraction. Towards this goal, we make two fundamental contributions: we extend MDP homomorphisms formalism to Convex RL, and we present, to the best of our knowledge, the first analysis that formally captures the benefit of abstraction via homomorphisms on sample efficiency. Ultimately, we propose the Geometric Active Exploration (GAE) algorithm, which we analyse theoretically and experimentally in environments motivated by problems in scientific discovery.

Global Reinforcement Learning: Beyond Linear and Convex Rewards via Submodular Semi-gradient Methods

In classic Reinforcement Learning (RL), the agent maximizes an additive objective of the visited states, e.g., a value function. Unfortunately, objectives of this type cannot model many real-world applications such as experiment design, exploration, imitation learning, and risk-averse RL to name a few. This is due to the fact that additive objectives disregard interactions between states that are crucial for certain tasks. To tackle this problem, we introduce Global RL (GRL), where rewards are globally defined over trajectories instead of locally over states. Global rewards can capture negative interactions among states, e.g., in exploration, via submodularity, positive interactions, e.g., synergetic effects, via supermodularity, while mixed interactions via combinations of them. By exploiting ideas from submodular optimization, we propose a novel algorithmic scheme that converts any GRL problem to a sequence of classic RL problems and solves it efficiently with curvature-dependent approximation guarantees. We also provide hardness of approximation results and empirically demonstrate the effectiveness of our method on several GRL instances.

Exploiting Causal Graph Priors with Posterior Sampling for Reinforcement Learning

Posterior sampling allows the exploitation of prior knowledge of the environment's transition dynamics to improve the sample efficiency of reinforcement learning. The prior is typically specified as a class of parametric distributions, a task that can be cumbersome in practice, often resulting in the choice of uninformative priors. In this work, we propose a novel posterior sampling approach in which the prior is given as a (partial) causal graph over the environment's variables. The latter is often more natural to design, such as listing known causal dependencies between biometric features in a medical treatment study. Specifically, we propose a hierarchical Bayesian procedure, called C-PSRL, simultaneously learning the full causal graph at the higher level and the parameters of the resulting factored dynamics at the lower level. For this procedure, we provide an analysis of its Bayesian regret, which explicitly connects the regret rate with the degree of prior knowledge. Our numerical evaluation conducted in illustrative domains confirms that C-PSRL strongly improves the efficiency of posterior sampling with an uninformative prior while performing close to posterior sampling with the full causal graph.

Provably Efficient Causal Model-Based Reinforcement Learning for Systematic Generalization

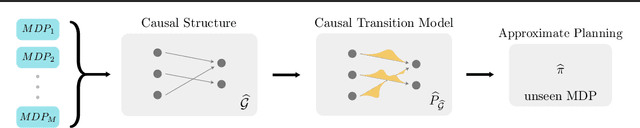
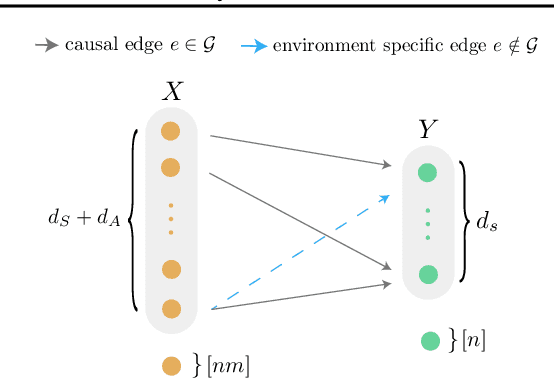
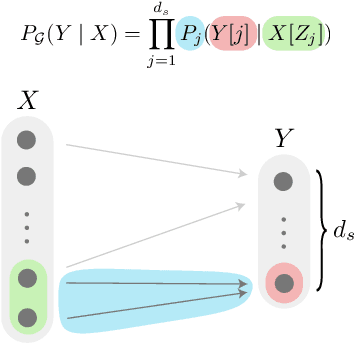
In the sequential decision making setting, an agent aims to achieve systematic generalization over a large, possibly infinite, set of environments. Such environments are modeled as discrete Markov decision processes with both states and actions represented through a feature vector. The underlying structure of the environments allows the transition dynamics to be factored into two components: one that is environment-specific and another one that is shared. Consider a set of environments that share the laws of motion as an illustrative example. In this setting, the agent can take a finite amount of reward-free interactions from a subset of these environments. The agent then must be able to approximately solve any planning task defined over any environment in the original set, relying on the above interactions only. Can we design a provably efficient algorithm that achieves this ambitious goal of systematic generalization? In this paper, we give a partially positive answer to this question. First, we provide the first tractable formulation of systematic generalization by employing a causal viewpoint. Then, under specific structural assumptions, we provide a simple learning algorithm that allows us to guarantee any desired planning error up to an unavoidable sub-optimality term, while showcasing a polynomial sample complexity.

The Importance of Non-Markovianity in Maximum State Entropy Exploration

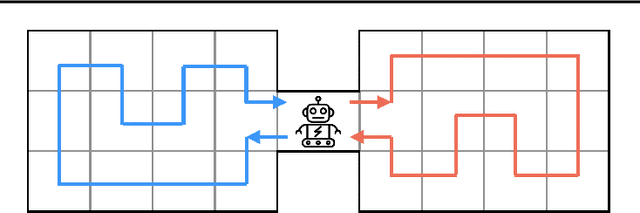
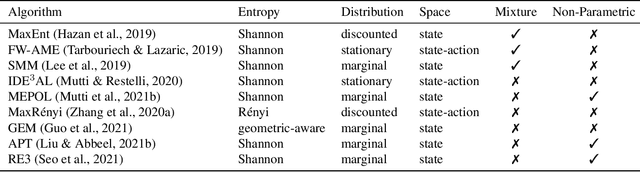
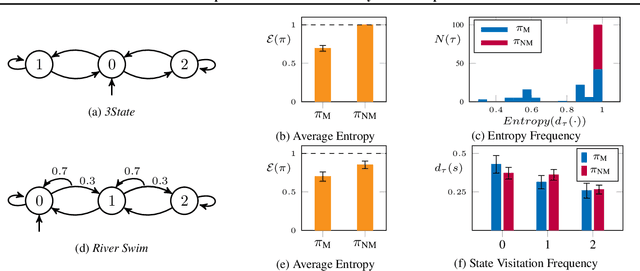
In the maximum state entropy exploration framework, an agent interacts with a reward-free environment to learn a policy that maximizes the entropy of the expected state visitations it is inducing. Hazan et al. (2019) noted that the class of Markovian stochastic policies is sufficient for the maximum state entropy objective, and exploiting non-Markovianity is generally considered pointless in this setting. In this paper, we argue that non-Markovianity is instead paramount for maximum state entropy exploration in a finite-sample regime. Especially, we recast the objective to target the expected entropy of the induced state visitations in a single trial. Then, we show that the class of non-Markovian deterministic policies is sufficient for the introduced objective, while Markovian policies suffer non-zero regret in general. However, we prove that the problem of finding an optimal non-Markovian policy is at least NP-complete. Despite this negative result, we discuss avenues to address the problem in a tractable way and how non-Markovian exploration could benefit the sample efficiency of online reinforcement learning in future works.

Challenging Common Assumptions in Convex Reinforcement Learning

The classic Reinforcement Learning (RL) formulation concerns the maximization of a scalar reward function. More recently, convex RL has been introduced to extend the RL formulation to all the objectives that are convex functions of the state distribution induced by a policy. Notably, convex RL covers several relevant applications that do not fall into the scalar formulation, including imitation learning, risk-averse RL, and pure exploration. In classic RL, it is common to optimize an infinite trials objective, which accounts for the state distribution instead of the empirical state visitation frequencies, even though the actual number of trajectories is always finite in practice. This is theoretically sound since the infinite trials and finite trials objectives can be proved to coincide and thus lead to the same optimal policy. In this paper, we show that this hidden assumption does not hold in the convex RL setting. In particular, we show that erroneously optimizing the infinite trials objective in place of the actual finite trials one, as it is usually done, can lead to a significant approximation error. Since the finite trials setting is the default in both simulated and real-world RL, we believe shedding light on this issue will lead to better approaches and methodologies for convex RL, impacting relevant research areas such as imitation learning, risk-averse RL, and pure exploration among others.