MM-Ego: Towards Building Egocentric Multimodal LLMs

This research aims to comprehensively explore building a multimodal foundation model for egocentric video understanding. To achieve this goal, we work on three fronts. First, as there is a lack of QA data for egocentric video understanding, we develop a data engine that efficiently generates 7M high-quality QA samples for egocentric videos ranging from 30 seconds to one hour long, based on human-annotated data. This is currently the largest egocentric QA dataset. Second, we contribute a challenging egocentric QA benchmark with 629 videos and 7,026 questions to evaluate the models' ability in recognizing and memorizing visual details across videos of varying lengths. We introduce a new de-biasing evaluation method to help mitigate the unavoidable language bias present in the models being evaluated. Third, we propose a specialized multimodal architecture featuring a novel "Memory Pointer Prompting" mechanism. This design includes a global glimpse step to gain an overarching understanding of the entire video and identify key visual information, followed by a fallback step that utilizes the key visual information to generate responses. This enables the model to more effectively comprehend extended video content. With the data, benchmark, and model, we successfully build MM-Ego, an egocentric multimodal LLM that shows powerful performance on egocentric video understanding.

Mobile V-MoEs: Scaling Down Vision Transformers via Sparse Mixture-of-Experts

Sparse Mixture-of-Experts models (MoEs) have recently gained popularity due to their ability to decouple model size from inference efficiency by only activating a small subset of the model parameters for any given input token. As such, sparse MoEs have enabled unprecedented scalability, resulting in tremendous successes across domains such as natural language processing and computer vision. In this work, we instead explore the use of sparse MoEs to scale-down Vision Transformers (ViTs) to make them more attractive for resource-constrained vision applications. To this end, we propose a simplified and mobile-friendly MoE design where entire images rather than individual patches are routed to the experts. We also propose a stable MoE training procedure that uses super-class information to guide the router. We empirically show that our sparse Mobile Vision MoEs (V-MoEs) can achieve a better trade-off between performance and efficiency than the corresponding dense ViTs. For example, for the ViT-Tiny model, our Mobile V-MoE outperforms its dense counterpart by 3.39% on ImageNet-1k. For an even smaller ViT variant with only 54M FLOPs inference cost, our MoE achieves an improvement of 4.66%.

Adapting the Linearised Laplace Model Evidence for Modern Deep Learning

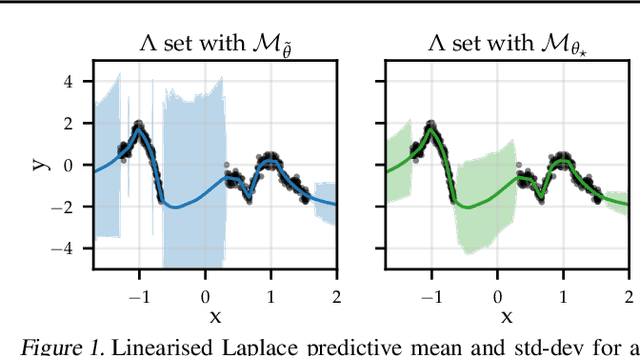
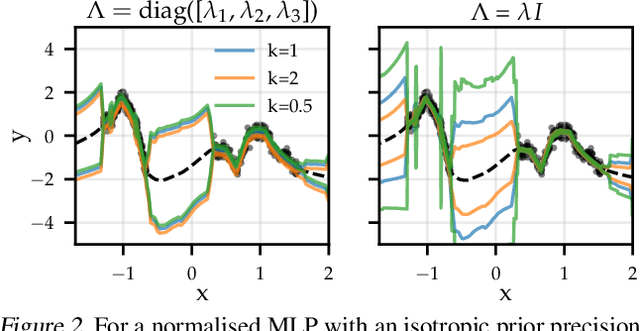
The linearised Laplace method for estimating model uncertainty has received renewed attention in the Bayesian deep learning community. The method provides reliable error bars and admits a closed-form expression for the model evidence, allowing for scalable selection of model hyperparameters. In this work, we examine the assumptions behind this method, particularly in conjunction with model selection. We show that these interact poorly with some now-standard tools of deep learning--stochastic approximation methods and normalisation layers--and make recommendations for how to better adapt this classic method to the modern setting. We provide theoretical support for our recommendations and validate them empirically on MLPs, classic CNNs, residual networks with and without normalisation layers, generative autoencoders and transformers.

Mixtures of Laplace Approximations for Improved Post-Hoc Uncertainty in Deep Learning

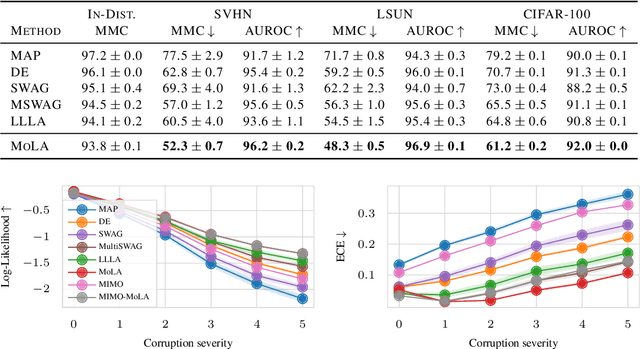
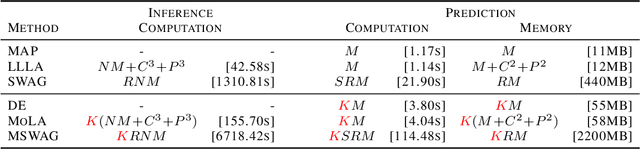
Deep neural networks are prone to overconfident predictions on outliers. Bayesian neural networks and deep ensembles have both been shown to mitigate this problem to some extent. In this work, we aim to combine the benefits of the two approaches by proposing to predict with a Gaussian mixture model posterior that consists of a weighted sum of Laplace approximations of independently trained deep neural networks. The method can be used post hoc with any set of pre-trained networks and only requires a small computational and memory overhead compared to regular ensembles. We theoretically validate that our approach mitigates overconfidence "far away" from the training data and empirically compare against state-of-the-art baselines on standard uncertainty quantification benchmarks.

Laplace Redux -- Effortless Bayesian Deep Learning

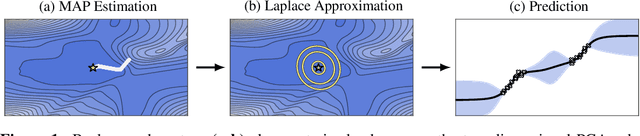
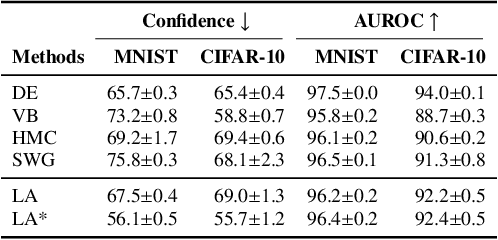
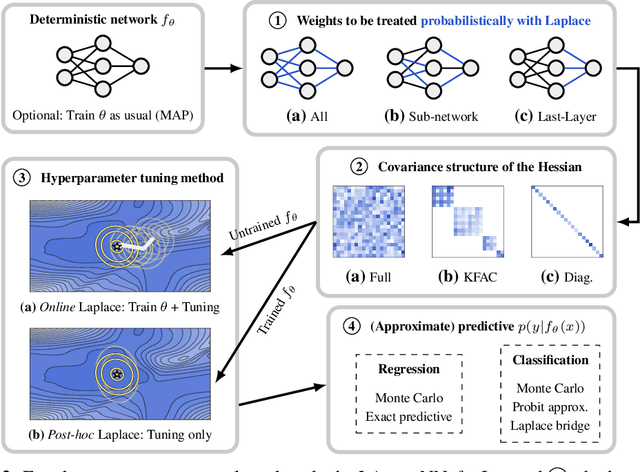
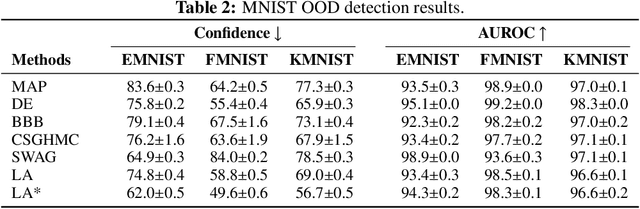
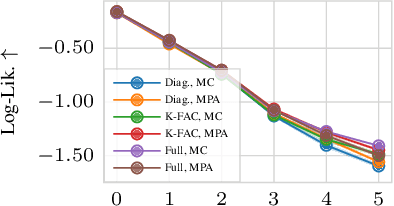
Bayesian formulations of deep learning have been shown to have compelling theoretical properties and offer practical functional benefits, such as improved predictive uncertainty quantification and model selection. The Laplace approximation (LA) is a classic, and arguably the simplest family of approximations for the intractable posteriors of deep neural networks. Yet, despite its simplicity, the LA is not as popular as alternatives like variational Bayes or deep ensembles. This may be due to assumptions that the LA is expensive due to the involved Hessian computation, that it is difficult to implement, or that it yields inferior results. In this work we show that these are misconceptions: we (i) review the range of variants of the LA including versions with minimal cost overhead; (ii) introduce "laplace", an easy-to-use software library for PyTorch offering user-friendly access to all major flavors of the LA; and (iii) demonstrate through extensive experiments that the LA is competitive with more popular alternatives in terms of performance, while excelling in terms of computational cost. We hope that this work will serve as a catalyst to a wider adoption of the LA in practical deep learning, including in domains where Bayesian approaches are not typically considered at the moment.

Expressive yet Tractable Bayesian Deep Learning via Subnetwork Inference

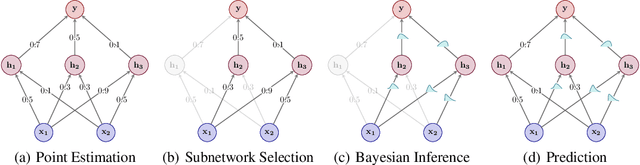
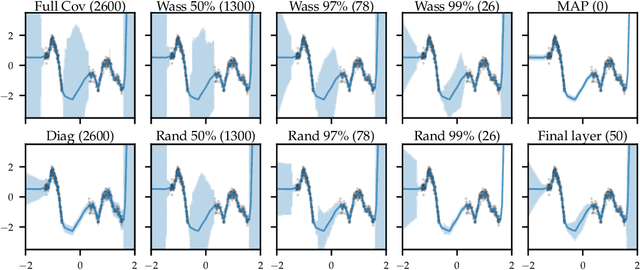
The Bayesian paradigm has the potential to solve some of the core issues in modern deep learning, such as poor calibration, data inefficiency, and catastrophic forgetting. However, scaling Bayesian inference to the high-dimensional parameter spaces of deep neural networks requires restrictive approximations. In this paper, we propose performing inference over only a small subset of the model parameters while keeping all others as point estimates. This enables us to use expressive posterior approximations that would otherwise be intractable for the full model. In particular, we develop a practical and scalable Bayesian deep learning method that first trains a point estimate, and then infers a full covariance Gaussian posterior approximation over a subnetwork. We propose a subnetwork selection procedure which aims to optimally preserve posterior uncertainty. We empirically demonstrate the effectiveness of our approach compared to point-estimated networks and methods that use less expressive posterior approximations over the full network.

Sample-Efficient Optimization in the Latent Space of Deep Generative Models via Weighted Retraining

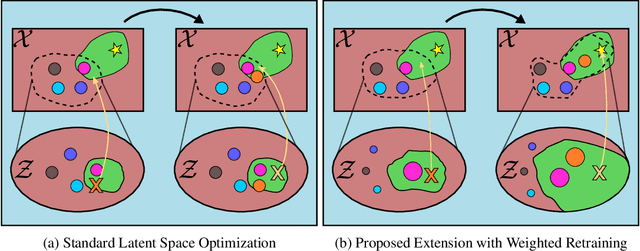
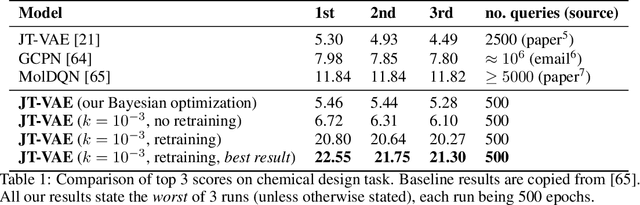
Many important problems in science and engineering, such as drug design, involve optimizing an expensive black-box objective function over a complex, high-dimensional, and structured input space. Although machine learning techniques have shown promise in solving such problems, existing approaches substantially lack sample efficiency. We introduce an improved method for efficient black-box optimization, which performs the optimization in the low-dimensional, continuous latent manifold learned by a deep generative model. In contrast to previous approaches, we actively steer the generative model to maintain a latent manifold that is highly useful for efficiently optimizing the objective. We achieve this by periodically retraining the generative model on the data points queried along the optimization trajectory, as well as weighting those data points according to their objective function value. This weighted retraining can be easily implemented on top of existing methods, and is empirically shown to significantly improve their efficiency and performance on synthetic and real-world optimization problems.

Bayesian Variational Autoencoders for Unsupervised Out-of-Distribution Detection

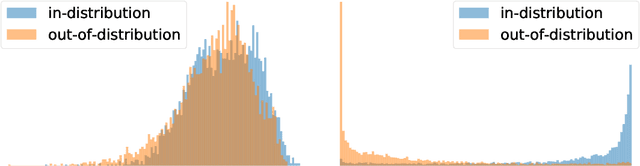
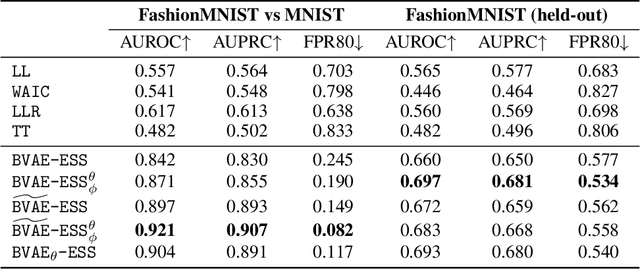
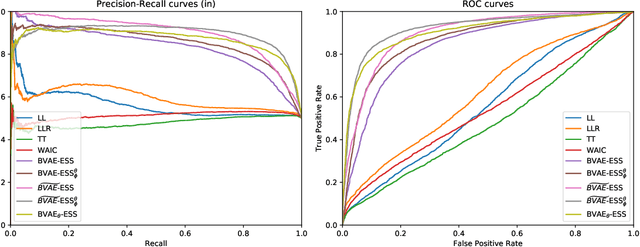
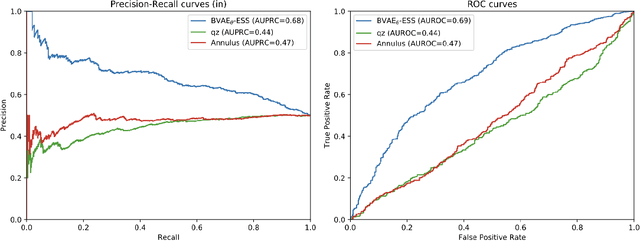
Despite their successes, deep neural networks still make unreliable predictions when faced with test data drawn from a distribution different to that of the training data, constituting a major problem for AI safety. While this motivated a recent surge in interest in developing methods to detect such out-of-distribution (OoD) inputs, a robust solution is still lacking. We propose a new probabilistic, unsupervised approach to this problem based on a Bayesian variational autoencoder model, which estimates a full posterior distribution over the decoder parameters using stochastic gradient Markov chain Monte Carlo, instead of fitting a point estimate. We describe how information-theoretic measures based on this posterior can then be used to detect OoD data both in input space as well as in the model's latent space. The effectiveness of our approach is empirically demonstrated.

Mixed-Variable Bayesian Optimization

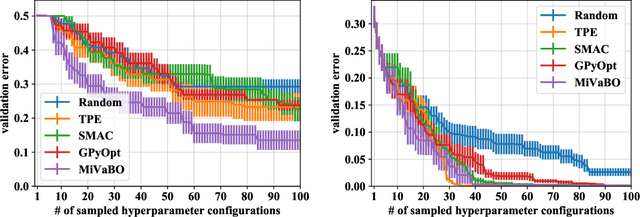
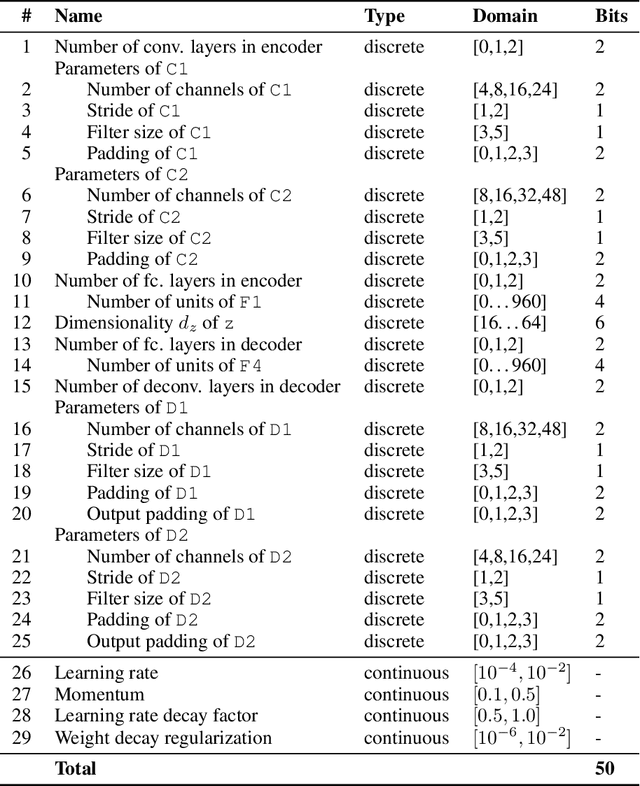
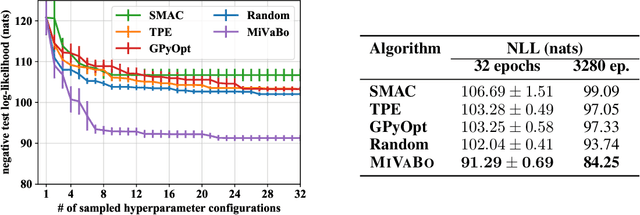
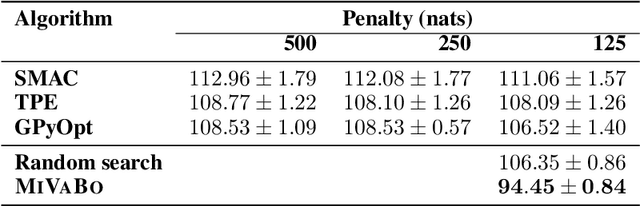
The optimization of expensive to evaluate, black-box, mixed-variable functions, i.e. functions that have continuous and discrete inputs, is a difficult and yet pervasive problem in science and engineering. In Bayesian optimization (BO), special cases of this problem that consider fully continuous or fully discrete domains have been widely studied. However, few methods exist for mixed-variable domains. In this paper, we introduce MiVaBo, a novel BO algorithm for the efficient optimization of mixed-variable functions that combines a linear surrogate model based on expressive feature representations with Thompson sampling. We propose two methods to optimize its acquisition function, a challenging problem for mixed-variable domains, and we show that MiVaBo can handle complex constraints over the discrete part of the domain that other methods cannot take into account. Moreover, we provide the first convergence analysis of a mixed-variable BO algorithm. Finally, we show that MiVaBo is significantly more sample efficient than state-of-the-art mixed-variable BO algorithms on hyperparameter tuning tasks.

Embedding Models for Episodic Memory

In recent years a number of large-scale triple-oriented knowledge graphs have been generated and various models have been proposed to perform learning in those graphs. Most knowledge graphs are static and reflect the world in its current state. In reality, of course, the state of the world is changing: a healthy person becomes diagnosed with a disease and a new president is inaugurated. In this paper, we extend models for static knowledge graphs to temporal knowledge graphs. This enables us to store episodic data and to generalize to new facts (inductive learning). We generalize leading learning models for static knowledge graphs (i.e., Tucker, RESCAL, HolE, ComplEx, DistMult) to temporal knowledge graphs. In particular, we introduce a new tensor model, ConT, with superior generalization performance. The performances of all proposed models are analyzed on two different datasets: the Global Database of Events, Language, and Tone (GDELT) and the database for Integrated Conflict Early Warning System (ICEWS). We argue that temporal knowledge graph embeddings might be models also for cognitive episodic memory (facts we remember and can recollect) and that a semantic memory (current facts we know) can be generated from episodic memory by a marginalization operation. We validate this episodic-to-semantic projection hypothesis with the ICEWS dataset.