Variational Inference of overparameterized Bayesian Neural Networks: a theoretical and empirical study

This paper studies the Variational Inference (VI) used for training Bayesian Neural Networks (BNN) in the overparameterized regime, i.e., when the number of neurons tends to infinity. More specifically, we consider overparameterized two-layer BNN and point out a critical issue in the mean-field VI training. This problem arises from the decomposition of the lower bound on the evidence (ELBO) into two terms: one corresponding to the likelihood function of the model and the second to the Kullback-Leibler (KL) divergence between the prior distribution and the variational posterior. In particular, we show both theoretically and empirically that there is a trade-off between these two terms in the overparameterized regime only when the KL is appropriately re-scaled with respect to the ratio between the the number of observations and neurons. We also illustrate our theoretical results with numerical experiments that highlight the critical choice of this ratio.

FedPop: A Bayesian Approach for Personalised Federated Learning

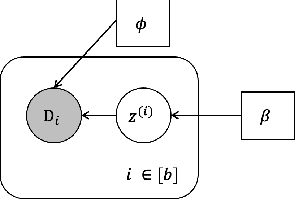
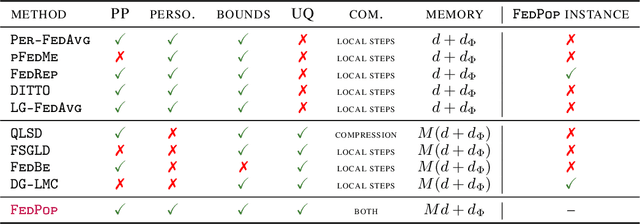
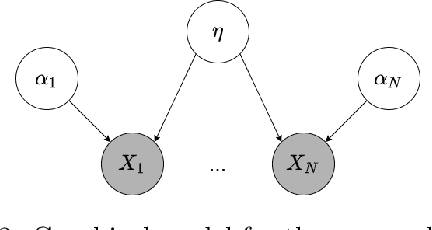
Personalised federated learning (FL) aims at collaboratively learning a machine learning model taylored for each client. Albeit promising advances have been made in this direction, most of existing approaches works do not allow for uncertainty quantification which is crucial in many applications. In addition, personalisation in the cross-device setting still involves important issues, especially for new clients or those having small number of observations. This paper aims at filling these gaps. To this end, we propose a novel methodology coined FedPop by recasting personalised FL into the population modeling paradigm where clients' models involve fixed common population parameters and random effects, aiming at explaining data heterogeneity. To derive convergence guarantees for our scheme, we introduce a new class of federated stochastic optimisation algorithms which relies on Markov chain Monte Carlo methods. Compared to existing personalised FL methods, the proposed methodology has important benefits: it is robust to client drift, practical for inference on new clients, and above all, enables uncertainty quantification under mild computational and memory overheads. We provide non-asymptotic convergence guarantees for the proposed algorithms and illustrate their performances on various personalised federated learning tasks.

From Dirichlet to Rubin: Optimistic Exploration in RL without Bonuses

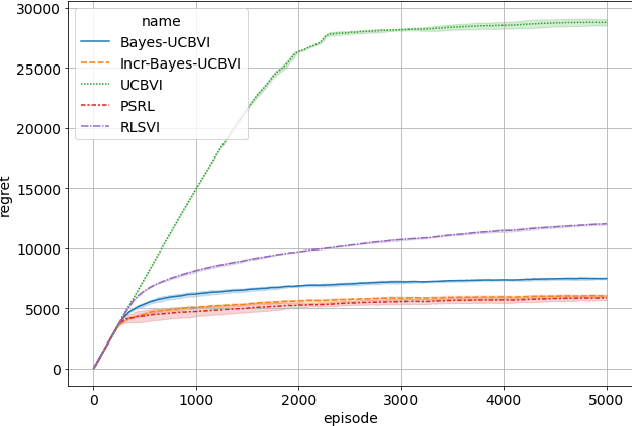
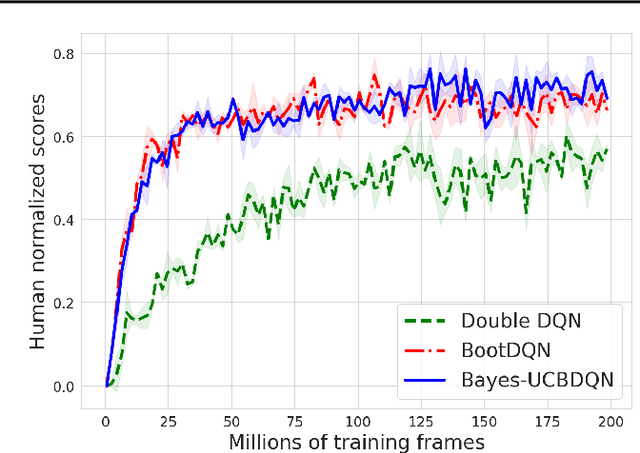
We propose the Bayes-UCBVI algorithm for reinforcement learning in tabular, stage-dependent, episodic Markov decision process: a natural extension of the Bayes-UCB algorithm by Kaufmann et al. (2012) for multi-armed bandits. Our method uses the quantile of a Q-value function posterior as upper confidence bound on the optimal Q-value function. For Bayes-UCBVI, we prove a regret bound of order $\widetilde{O}(\sqrt{H^3SAT})$ where $H$ is the length of one episode, $S$ is the number of states, $A$ the number of actions, $T$ the number of episodes, that matches the lower-bound of $\Omega(\sqrt{H^3SAT})$ up to poly-$\log$ terms in $H,S,A,T$ for a large enough $T$. To the best of our knowledge, this is the first algorithm that obtains an optimal dependence on the horizon $H$ (and $S$) without the need for an involved Bernstein-like bonus or noise. Crucial to our analysis is a new fine-grained anti-concentration bound for a weighted Dirichlet sum that can be of independent interest. We then explain how Bayes-UCBVI can be easily extended beyond the tabular setting, exhibiting a strong link between our algorithm and Bayesian bootstrap (Rubin, 1981).

Diffusion bridges vector quantized Variational AutoEncoders

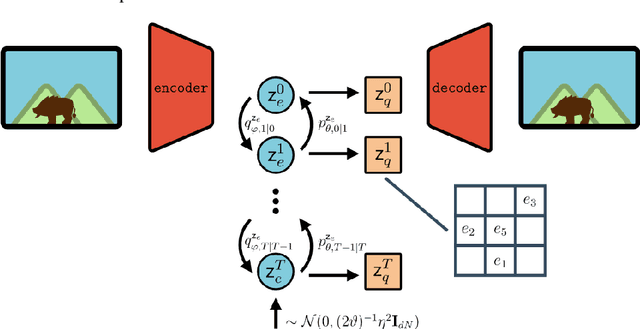
Vector Quantised-Variational AutoEncoders (VQ-VAE) are generative models based on discrete latent representations of the data, where inputs are mapped to a finite set of learned embeddings.To generate new samples, an autoregressive prior distribution over the discrete states must be trained separately. This prior is generally very complex and leads to very slow generation. In this work, we propose a new model to train the prior and the encoder/decoder networks simultaneously. We build a diffusion bridge between a continuous coded vector and a non-informative prior distribution. The latent discrete states are then given as random functions of these continuous vectors. We show that our model is competitive with the autoregressive prior on the mini-Imagenet dataset and is very efficient in both optimization and sampling. Our framework also extends the standard VQ-VAE and enables end-to-end training.

Federated Expectation Maximization with heterogeneity mitigation and variance reduction

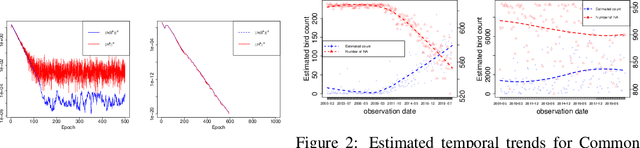
The Expectation Maximization (EM) algorithm is the default algorithm for inference in latent variable models. As in any other field of machine learning, applications of latent variable models to very large datasets make the use of advanced parallel and distributed architectures mandatory. This paper introduces FedEM, which is the first extension of the EM algorithm to the federated learning context. FedEM is a new communication efficient method, which handles partial participation of local devices, and is robust to heterogeneous distributions of the datasets. To alleviate the communication bottleneck, FedEM compresses appropriately defined complete data sufficient statistics. We also develop and analyze an extension of FedEM to further incorporate a variance reduction scheme. In all cases, we derive finite-time complexity bounds for smooth non-convex problems. Numerical results are presented to support our theoretical findings, as well as an application to federated missing values imputation for biodiversity monitoring.

Ex$^2$MCMC: Sampling through Exploration Exploitation

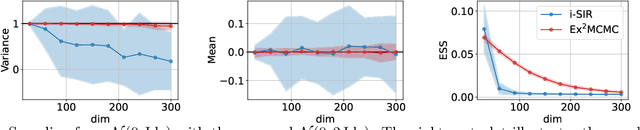
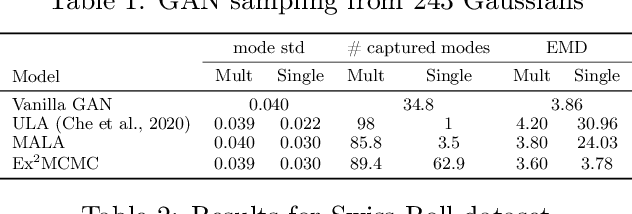
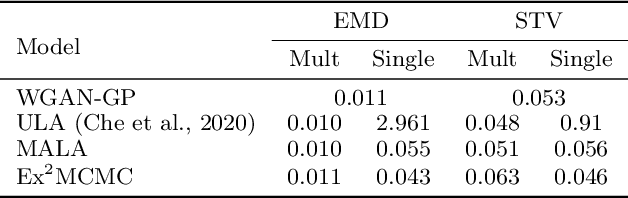
We develop an Explore-Exploit Markov chain Monte Carlo algorithm ($\operatorname{Ex^2MCMC}$) that combines multiple global proposals and local moves. The proposed method is massively parallelizable and extremely computationally efficient. We prove $V$-uniform geometric ergodicity of $\operatorname{Ex^2MCMC}$ under realistic conditions and compute explicit bounds on the mixing rate showing the improvement brought by the multiple global moves. We show that $\operatorname{Ex^2MCMC}$ allows fine-tuning of exploitation (local moves) and exploration (global moves) via a novel approach to proposing dependent global moves. Finally, we develop an adaptive scheme, $\operatorname{FlEx^2MCMC}$, that learns the distribution of global moves using normalizing flows. We illustrate the efficiency of $\operatorname{Ex^2MCMC}$ and its adaptive versions on many classical sampling benchmarks. We also show that these algorithms improve the quality of sampling GANs as energy-based models.

Monte Carlo Variational Auto-Encoders

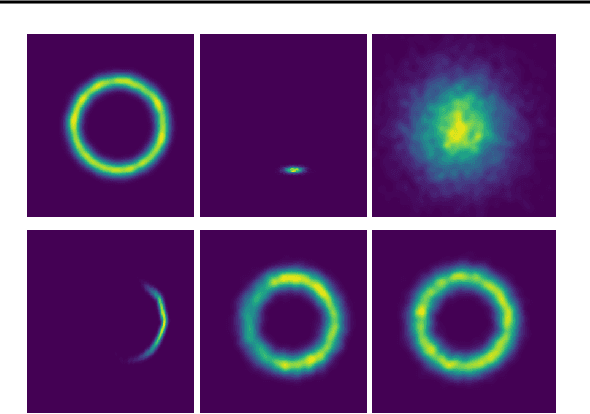
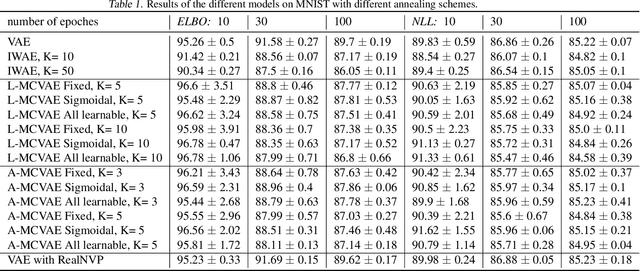
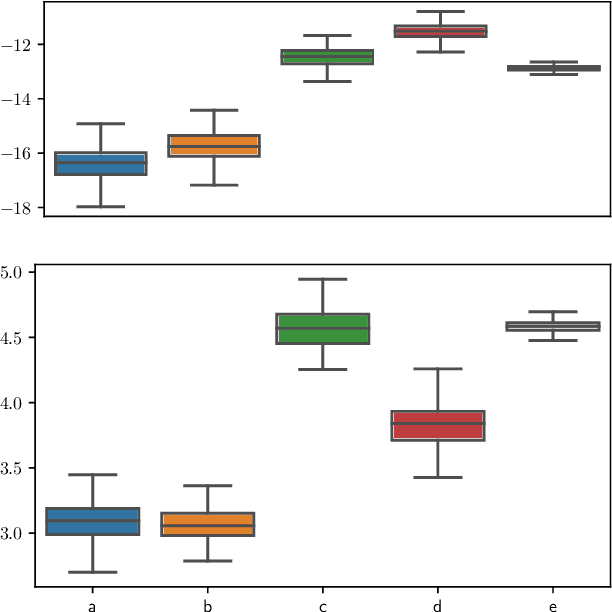
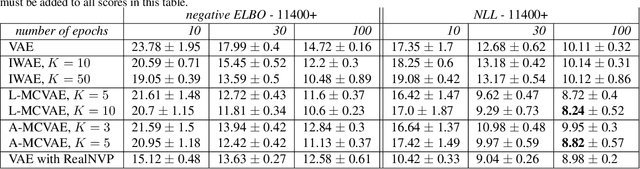
Variational auto-encoders (VAE) are popular deep latent variable models which are trained by maximizing an Evidence Lower Bound (ELBO). To obtain tighter ELBO and hence better variational approximations, it has been proposed to use importance sampling to get a lower variance estimate of the evidence. However, importance sampling is known to perform poorly in high dimensions. While it has been suggested many times in the literature to use more sophisticated algorithms such as Annealed Importance Sampling (AIS) and its Sequential Importance Sampling (SIS) extensions, the potential benefits brought by these advanced techniques have never been realized for VAE: the AIS estimate cannot be easily differentiated, while SIS requires the specification of carefully chosen backward Markov kernels. In this paper, we address both issues and demonstrate the performance of the resulting Monte Carlo VAEs on a variety of applications.

DG-LMC: A Turn-key and Scalable Synchronous Distributed MCMC Algorithm via Langevin Monte Carlo within Gibbs

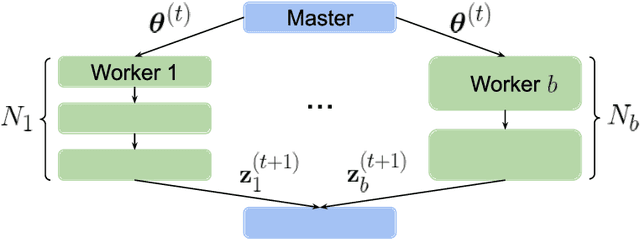
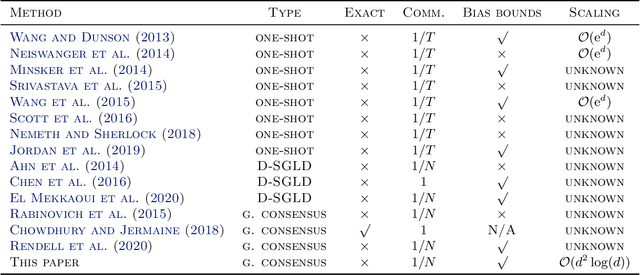
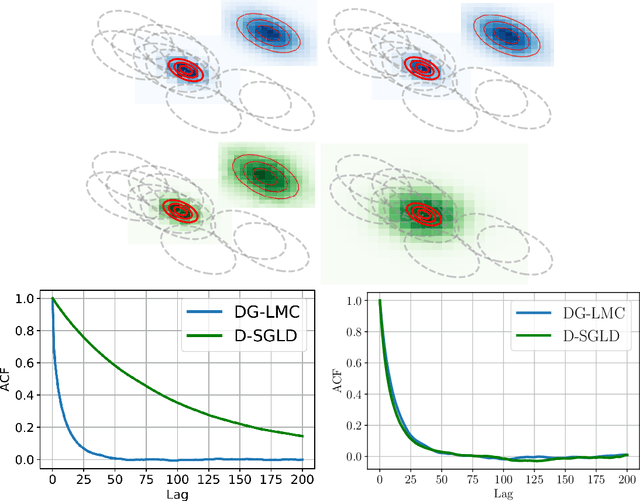
Performing reliable Bayesian inference on a big data scale is becoming a keystone in the modern era of machine learning. A workhorse class of methods to achieve this task are Markov chain Monte Carlo (MCMC) algorithms and their design to handle distributed datasets has been the subject of many works. However, existing methods are not completely either reliable or computationally efficient. In this paper, we propose to fill this gap in the case where the dataset is partitioned and stored on computing nodes within a cluster under a master/slaves architecture. We derive a user-friendly centralised distributed MCMC algorithm with provable scaling in high-dimensional settings. We illustrate the relevance of the proposed methodology on both synthetic and real data experiments.

Tight High Probability Bounds for Linear Stochastic Approximation with Fixed Stepsize

This paper provides a non-asymptotic analysis of linear stochastic approximation (LSA) algorithms with fixed stepsize. This family of methods arises in many machine learning tasks and is used to obtain approximate solutions of a linear system $\bar{A}\theta = \bar{b}$ for which $\bar{A}$ and $\bar{b}$ can only be accessed through random estimates $\{({\bf A}_n, {\bf b}_n): n \in \mathbb{N}^*\}$. Our analysis is based on new results regarding moments and high probability bounds for products of matrices which are shown to be tight. We derive high probability bounds on the performance of LSA under weaker conditions on the sequence $\{({\bf A}_n, {\bf b}_n): n \in \mathbb{N}^*\}$ than previous works. However, in contrast, we establish polynomial concentration bounds with order depending on the stepsize. We show that our conclusions cannot be improved without additional assumptions on the sequence of random matrices $\{{\bf A}_n: n \in \mathbb{N}^*\}$, and in particular that no Gaussian or exponential high probability bounds can hold. Finally, we pay a particular attention to establishing bounds with sharp order with respect to the number of iterations and the stepsize and whose leading terms contain the covariance matrices appearing in the central limit theorems.

QLSD: Quantised Langevin stochastic dynamics for Bayesian federated learning

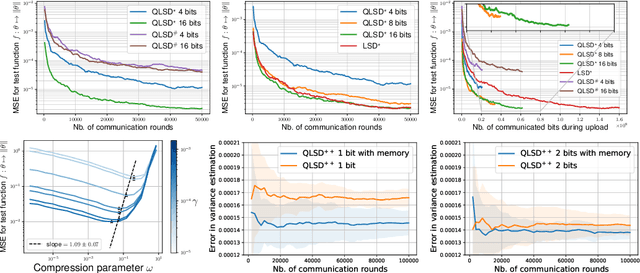
Federated learning aims at conducting inference when data are decentralised and locally stored on several clients, under two main constraints: data ownership and communication overhead. In this paper, we address these issues under the Bayesian paradigm. To this end, we propose a novel Markov chain Monte Carlo algorithm coined \texttt{QLSD} built upon quantised versions of stochastic gradient Langevin dynamics. To improve performance in a big data regime, we introduce variance-reduced alternatives of our methodology referred to as \texttt{QLSD}$^\star$ and \texttt{QLSD}$^{++}$. We provide both non-asymptotic and asymptotic convergence guarantees for the proposed algorithms and illustrate their benefits on several federated learning benchmarks.