A Bregman firmly nonexpansive proximal operator for baryconvex optimization

We present a generalization of the proximal operator defined through a convex combination of convex objectives, where the coefficients are updated in a minimax fashion. We prove that this new operator is Bregman firmly nonexpansive with respect to a Bregman divergence that combines Euclidean and information geometries.

Investigating Regularization of Self-Play Language Models

This paper explores the effects of various forms of regularization in the context of language model alignment via self-play. While both reinforcement learning from human feedback (RLHF) and direct preference optimization (DPO) require to collect costly human-annotated pairwise preferences, the self-play fine-tuning (SPIN) approach replaces the rejected answers by data generated from the previous iterate. However, the SPIN method presents a performance instability issue in the learning phase, which can be mitigated by playing against a mixture of the two previous iterates. In the same vein, we propose in this work to address this issue from two perspectives: first, by incorporating an additional Kullback-Leibler (KL) regularization to stay at the proximity of the reference policy; second, by using the idea of fictitious play which smoothens the opponent policy across all previous iterations. In particular, we show that the KL-based regularizer boils down to replacing the previous policy by its geometric mixture with the base policy inside of the SPIN loss function. We finally discuss empirical results on MT-Bench as well as on the Hugging Face Open LLM Leaderboard.

A Risk-Averse Framework for Non-Stationary Stochastic Multi-Armed Bandits

In a typical stochastic multi-armed bandit problem, the objective is often to maximize the expected sum of rewards over some time horizon $T$. While the choice of a strategy that accomplishes that is optimal with no additional information, it is no longer the case when provided additional environment-specific knowledge. In particular, in areas of high volatility like healthcare or finance, a naive reward maximization approach often does not accurately capture the complexity of the learning problem and results in unreliable solutions. To tackle problems of this nature, we propose a framework of adaptive risk-aware strategies that operate in non-stationary environments. Our framework incorporates various risk measures prevalent in the literature to map multiple families of multi-armed bandit algorithms into a risk-sensitive setting. In addition, we equip the resulting algorithms with the Restarted Bayesian Online Change-Point Detection (R-BOCPD) algorithm and impose a (tunable) forced exploration strategy to detect local (per-arm) switches. We provide finite-time theoretical guarantees and an asymptotic regret bound of order $\tilde O(\sqrt{K_T T})$ up to time horizon $T$ with $K_T$ the total number of change-points. In practice, our framework compares favorably to the state-of-the-art in both synthetic and real-world environments and manages to perform efficiently with respect to both risk-sensitivity and non-stationarity.

Deep Reinforcement Learning Algorithms for Hybrid V2X Communication: A Benchmarking Study

In today's era, autonomous vehicles demand a safety level on par with aircraft. Taking a cue from the aerospace industry, which relies on redundancy to achieve high reliability, the automotive sector can also leverage this concept by building redundancy in V2X (Vehicle-to-Everything) technologies. Given the current lack of reliable V2X technologies, this idea is particularly promising. By deploying multiple RATs (Radio Access Technologies) in parallel, the ongoing debate over the standard technology for future vehicles can be put to rest. However, coordinating multiple communication technologies is a complex task due to dynamic, time-varying channels and varying traffic conditions. This paper addresses the vertical handover problem in V2X using Deep Reinforcement Learning (DRL) algorithms. The goal is to assist vehicles in selecting the most appropriate V2X technology (DSRC/V-VLC) in a serpentine environment. The results show that the benchmarked algorithms outperform the current state-of-the-art approaches in terms of redundancy and usage rate of V-VLC headlights. This result is a significant reduction in communication costs while maintaining a high level of reliability. These results provide strong evidence for integrating advanced DRL decision mechanisms into the architecture as a promising approach to solving the vertical handover problem in V2X.

Beyond Log-Concavity: Theory and Algorithm for Sum-Log-Concave Optimization

This paper extends the classic theory of convex optimization to the minimization of functions that are equal to the negated logarithm of what we term as a sum-log-concave function, i.e., a sum of log-concave functions. In particular, we show that such functions are in general not convex but still satisfy generalized convexity inequalities. These inequalities unveil the key importance of a certain vector that we call the cross-gradient and that is, in general, distinct from the usual gradient. Thus, we propose the Cross Gradient Descent (XGD) algorithm moving in the opposite direction of the cross-gradient and derive a convergence analysis. As an application of our sum-log-concave framework, we introduce the so-called checkered regression method relying on a sum-log-concave function. This classifier extends (multiclass) logistic regression to non-linearly separable problems since it is capable of tessellating the feature space by using any given number of hyperplanes, creating a checkerboard-like pattern of decision regions.

A Nested Matrix-Tensor Model for Noisy Multi-view Clustering

In this paper, we propose a nested matrix-tensor model which extends the spiked rank-one tensor model of order three. This model is particularly motivated by a multi-view clustering problem in which multiple noisy observations of each data point are acquired, with potentially non-uniform variances along the views. In this case, data can be naturally represented by an order-three tensor where the views are stacked. Given such a tensor, we consider the estimation of the hidden clusters via performing a best rank-one tensor approximation. In order to study the theoretical performance of this approach, we characterize the behavior of this best rank-one approximation in terms of the alignments of the obtained component vectors with the hidden model parameter vectors, in the large-dimensional regime. In particular, we show that our theoretical results allow us to anticipate the exact accuracy of the proposed clustering approach. Furthermore, numerical experiments indicate that leveraging our tensor-based approach yields better accuracy compared to a naive unfolding-based algorithm which ignores the underlying low-rank tensor structure. Our analysis unveils unexpected and non-trivial phase transition phenomena depending on the model parameters, ``interpolating'' between the typical behavior observed for the spiked matrix and tensor models.

One-Step Distributional Reinforcement Learning

Reinforcement learning (RL) allows an agent interacting sequentially with an environment to maximize its long-term expected return. In the distributional RL (DistrRL) paradigm, the agent goes beyond the limit of the expected value, to capture the underlying probability distribution of the return across all time steps. The set of DistrRL algorithms has led to improved empirical performance. Nevertheless, the theory of DistrRL is still not fully understood, especially in the control case. In this paper, we present the simpler one-step distributional reinforcement learning (OS-DistrRL) framework encompassing only the randomness induced by the one-step dynamics of the environment. Contrary to DistrRL, we show that our approach comes with a unified theory for both policy evaluation and control. Indeed, we propose two OS-DistrRL algorithms for which we provide an almost sure convergence analysis. The proposed approach compares favorably with categorical DistrRL on various environments.

Robustness and risk management via distributional dynamic programming

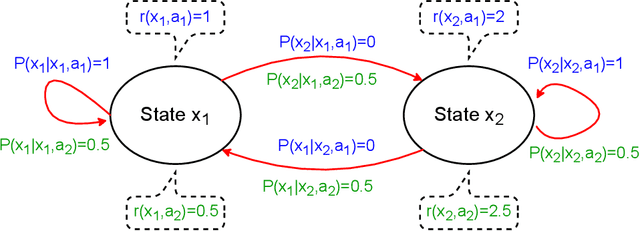
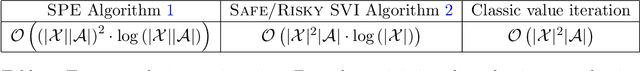
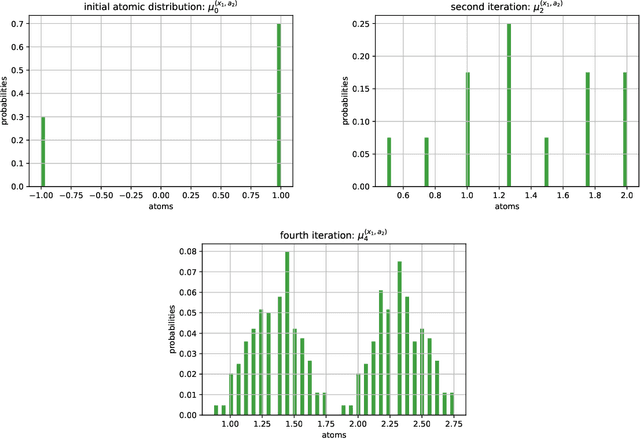
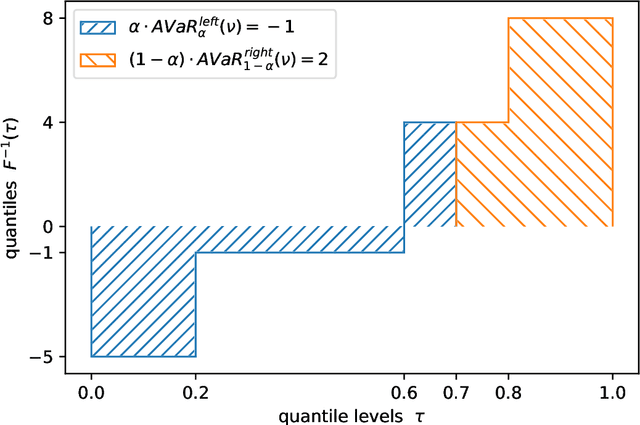
In dynamic programming (DP) and reinforcement learning (RL), an agent learns to act optimally in terms of expected long-term return by sequentially interacting with its environment modeled by a Markov decision process (MDP). More generally in distributional reinforcement learning (DRL), the focus is on the whole distribution of the return, not just its expectation. Although DRL-based methods produced state-of-the-art performance in RL with function approximation, they involve additional quantities (compared to the non-distributional setting) that are still not well understood. As a first contribution, we introduce a new class of distributional operators, together with a practical DP algorithm for policy evaluation, that come with a robust MDP interpretation. Indeed, our approach reformulates through an augmented state space where each state is split into a worst-case substate and a best-case substate, whose values are maximized by safe and risky policies respectively. Finally, we derive distributional operators and DP algorithms solving a new control task: How to distinguish safe from risky optimal actions in order to break ties in the space of optimal policies?

Weighted Empirical Risk Minimization: Sample Selection Bias Correction based on Importance Sampling

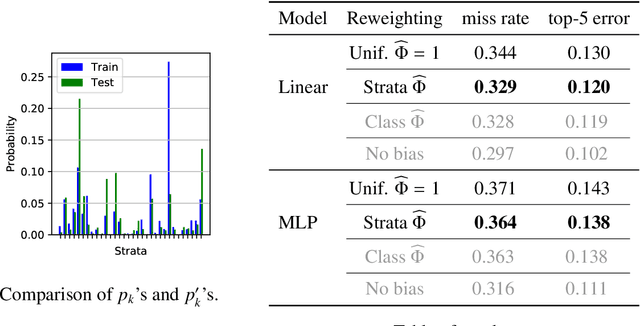
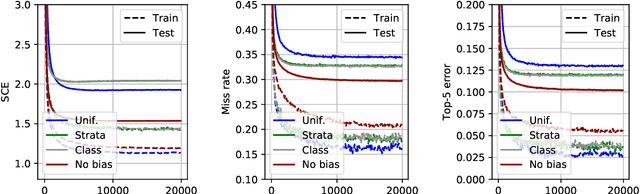
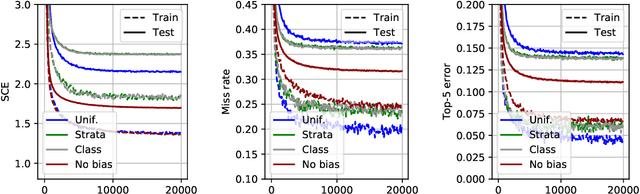
We consider statistical learning problems, when the distribution $P'$ of the training observations $Z'_1,\; \ldots,\; Z'_n$ differs from the distribution $P$ involved in the risk one seeks to minimize (referred to as the test distribution) but is still defined on the same measurable space as $P$ and dominates it. In the unrealistic case where the likelihood ratio $\Phi(z)=dP/dP'(z)$ is known, one may straightforwardly extends the Empirical Risk Minimization (ERM) approach to this specific transfer learning setup using the same idea as that behind Importance Sampling, by minimizing a weighted version of the empirical risk functional computed from the 'biased' training data $Z'_i$ with weights $\Phi(Z'_i)$. Although the importance function $\Phi(z)$ is generally unknown in practice, we show that, in various situations frequently encountered in practice, it takes a simple form and can be directly estimated from the $Z'_i$'s and some auxiliary information on the statistical population $P$. By means of linearization techniques, we then prove that the generalization capacity of the approach aforementioned is preserved when plugging the resulting estimates of the $\Phi(Z'_i)$'s into the weighted empirical risk. Beyond these theoretical guarantees, numerical results provide strong empirical evidence of the relevance of the approach promoted in this article.

Dimensionality Reduction and (Bucket) Ranking: a Mass Transportation Approach

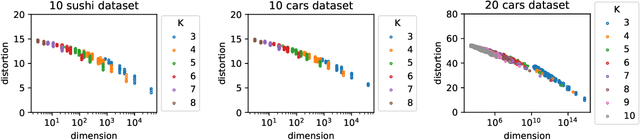
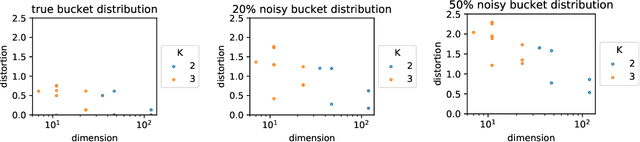
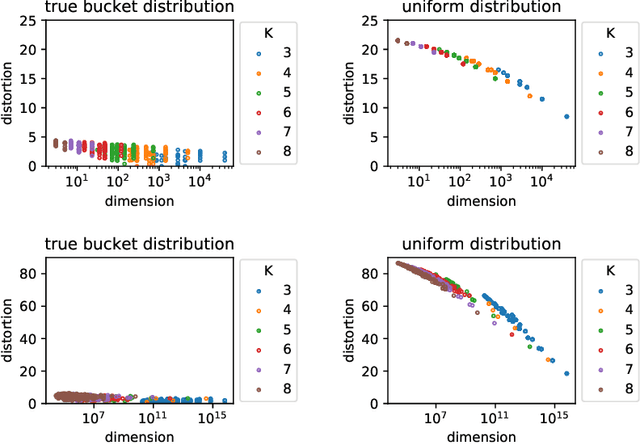
Whereas most dimensionality reduction techniques (e.g. PCA, ICA, NMF) for multivariate data essentially rely on linear algebra to a certain extent, summarizing ranking data, viewed as realizations of a random permutation $\Sigma$ on a set of items indexed by $i\in \{1,\ldots,\; n\}$, is a great statistical challenge, due to the absence of vector space structure for the set of permutations $\mathfrak{S}_n$. It is the goal of this article to develop an original framework for possibly reducing the number of parameters required to describe the distribution of a statistical population composed of rankings/permutations, on the premise that the collection of items under study can be partitioned into subsets/buckets, such that, with high probability, items in a certain bucket are either all ranked higher or else all ranked lower than items in another bucket. In this context, $\Sigma$'s distribution can be hopefully represented in a sparse manner by a bucket distribution, i.e. a bucket ordering plus the ranking distributions within each bucket. More precisely, we introduce a dedicated distortion measure, based on a mass transportation metric, in order to quantify the accuracy of such representations. The performance of buckets minimizing an empirical version of the distortion is investigated through a rate bound analysis. Complexity penalization techniques are also considered to select the shape of a bucket order with minimum expected distortion. Beyond theoretical concepts and results, numerical experiments on real ranking data are displayed in order to provide empirical evidence of the relevance of the approach promoted.