SignSVRG: fixing SignSGD via variance reduction

We consider the problem of unconstrained minimization of finite sums of functions. We propose a simple, yet, practical way to incorporate variance reduction techniques into SignSGD, guaranteeing convergence that is similar to the full sign gradient descent. The core idea is first instantiated on the problem of minimizing sums of convex and Lipschitz functions and is then extended to the smooth case via variance reduction. Our analysis is elementary and much simpler than the typical proof for variance reduction methods. We show that for smooth functions our method gives $\mathcal{O}(1 / \sqrt{T})$ rate for expected norm of the gradient and $\mathcal{O}(1/T)$ rate in the case of smooth convex functions, recovering convergence results of deterministic methods, while preserving computational advantages of SignSGD.

Orthogonal Directions Constrained Gradient Method: from non-linear equality constraints to Stiefel manifold

We consider the problem of minimizing a non-convex function over a smooth manifold $\mathcal{M}$. We propose a novel algorithm, the Orthogonal Directions Constrained Gradient Method (ODCGM) which only requires computing a projection onto a vector space. ODCGM is infeasible but the iterates are constantly pulled towards the manifold, ensuring the convergence of ODCGM towards $\mathcal{M}$. ODCGM is much simpler to implement than the classical methods which require the computation of a retraction. Moreover, we show that ODCGM exhibits the near-optimal oracle complexities $\mathcal{O}(1/\varepsilon^2)$ and $\mathcal{O}(1/\varepsilon^4)$ in the deterministic and stochastic cases, respectively. Furthermore, we establish that, under an appropriate choice of the projection metric, our method recovers the landing algorithm of Ablin and Peyr\'e (2022), a recently introduced algorithm for optimization over the Stiefel manifold. As a result, we significantly extend the analysis of Ablin and Peyr\'e (2022), establishing near-optimal rates both in deterministic and stochastic frameworks. Finally, we perform numerical experiments which shows the efficiency of ODCGM in a high-dimensional setting.

AskewSGD : An Annealed interval-constrained Optimisation method to train Quantized Neural Networks

In this paper, we develop a new algorithm, Annealed Skewed SGD - AskewSGD - for training deep neural networks (DNNs) with quantized weights. First, we formulate the training of quantized neural networks (QNNs) as a smoothed sequence of interval-constrained optimization problems. Then, we propose a new first-order stochastic method, AskewSGD, to solve each constrained optimization subproblem. Unlike algorithms with active sets and feasible directions, AskewSGD avoids projections or optimization under the entire feasible set and allows iterates that are infeasible. The numerical complexity of AskewSGD is comparable to existing approaches for training QNNs, such as the straight-through gradient estimator used in BinaryConnect, or other state of the art methods (ProxQuant, LUQ). We establish convergence guarantees for AskewSGD (under general assumptions for the objective function). Experimental results show that the AskewSGD algorithm performs better than or on par with state of the art methods in classical benchmarks.

Stochastic Subgradient Descent on a Generic Definable Function Converges to a Minimizer

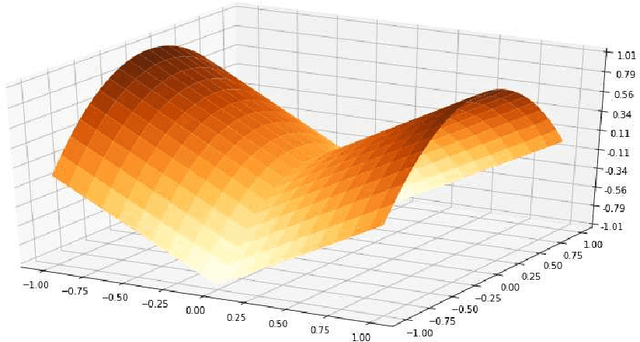
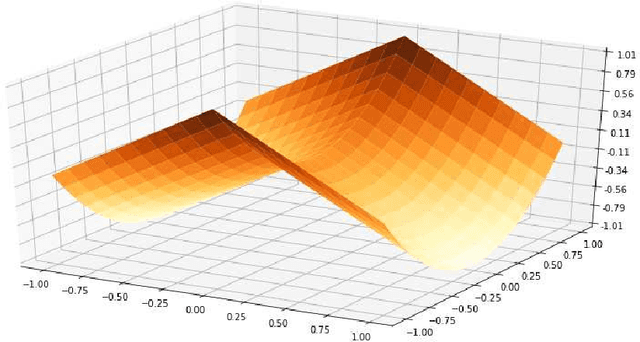
It was previously shown by Davis and Drusvyatskiy that every Clarke critical point of a generic, semialgebraic (and more generally definable in an o-minimal structure), weakly convex function is lying on an active manifold and is either a local minimum or an active strict saddle. In the first part of this work, we show that when the weak convexity assumption fails a third type of point appears: a sharply repulsive critical point. Moreover, we show that the corresponding active manifolds satisfy the Verdier and the angle conditions which were introduced by us in our previous work. In the second part of this work, we show that, under a density-like assumption on the perturbation sequence, the stochastic subgradient descent (SGD) avoids sharply repulsive critical points with probability one. We show that such a density-like assumption could be obtained upon adding a small random perturbation (e.g. a nondegenerate Gaussian) at each iteration of the algorithm. These results, combined with our previous work on the avoidance of active strict saddles, show that the SGD on a generic definable (e.g. semialgebraic) function converges to a local minimum.

Stochastic Subgradient Descent Escapes Active Strict Saddles

In non-smooth stochastic optimization, we establish the non-convergence of the stochastic subgradient descent (SGD) to the critical points recently called active strict saddles by Davis and Drusvyatskiy. Such points lie on a manifold $M$ where the function $f$ has a direction of second-order negative curvature. Off this manifold, the norm of the Clarke subdifferential of $f$ is lower-bounded. We require two conditions on $f$. The first assumption is a Verdier stratification condition, which is a refinement of the popular Whitney stratification. It allows us to establish a reinforced version of the projection formula of Bolte \emph{et.al.} for Whitney stratifiable functions, and which is of independent interest. The second assumption, termed the angle condition, allows to control the distance of the iterates to $M$. When $f$ is weakly convex, our assumptions are generic. Consequently, generically in the class of definable weakly convex functions, the SGD converges to a local minimizer.