On the Power of Decision Trees in Auto-Regressive Language Modeling

Originally proposed for handling time series data, Auto-regressive Decision Trees (ARDTs) have not yet been explored for language modeling. This paper delves into both the theoretical and practical applications of ARDTs in this new context. We theoretically demonstrate that ARDTs can compute complex functions, such as simulating automata, Turing machines, and sparse circuits, by leveraging "chain-of-thought" computations. Our analysis provides bounds on the size, depth, and computational efficiency of ARDTs, highlighting their surprising computational power. Empirically, we train ARDTs on simple language generation tasks, showing that they can learn to generate coherent and grammatically correct text on par with a smaller Transformer model. Additionally, we show that ARDTs can be used on top of transformer representations to solve complex reasoning tasks. This research reveals the unique computational abilities of ARDTs, aiming to broaden the architectural diversity in language model development.

Universal Length Generalization with Turing Programs

Length generalization refers to the ability to extrapolate from short training sequences to long test sequences and is a challenge for current large language models. While prior work has proposed some architecture or data format changes to achieve length generalization, these proposals typically apply to a limited set of tasks. Building on prior scratchpad and Chain-of-Thought (CoT) techniques, we propose Turing Programs, a novel CoT strategy that decomposes an algorithmic task into steps mimicking the computation of a Turing Machine. This framework is both universal, as it can accommodate any algorithmic task, and simple, requiring only copying text from the context with small modifications. We show that by using Turing Programs, we obtain robust length generalization on a range of algorithmic tasks: addition, multiplication and in-context SGD. We then demonstrate that transformers achieve length generalization on random Turing Programs, suggesting that length generalization is possible for any algorithmic task. Finally, we theoretically prove that transformers can implement Turing Programs, constructing a simple RASP (Weiss et al.) program that simulates an arbitrary Turing machine.

A New Perspective on Shampoo's Preconditioner

Shampoo, a second-order optimization algorithm which uses a Kronecker product preconditioner, has recently garnered increasing attention from the machine learning community. The preconditioner used by Shampoo can be viewed either as an approximation of the Gauss--Newton component of the Hessian or the covariance matrix of the gradients maintained by Adagrad. We provide an explicit and novel connection between the $\textit{optimal}$ Kronecker product approximation of these matrices and the approximation made by Shampoo. Our connection highlights a subtle but common misconception about Shampoo's approximation. In particular, the $\textit{square}$ of the approximation used by the Shampoo optimizer is equivalent to a single step of the power iteration algorithm for computing the aforementioned optimal Kronecker product approximation. Across a variety of datasets and architectures we empirically demonstrate that this is close to the optimal Kronecker product approximation. Additionally, for the Hessian approximation viewpoint, we empirically study the impact of various practical tricks to make Shampoo more computationally efficient (such as using the batch gradient and the empirical Fisher) on the quality of Hessian approximation.

Transcendence: Generative Models Can Outperform The Experts That Train Them

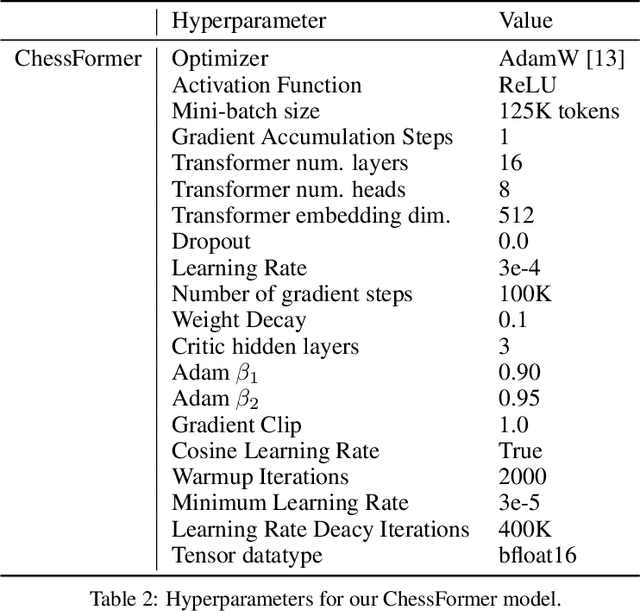
Generative models are trained with the simple objective of imitating the conditional probability distribution induced by the data they are trained on. Therefore, when trained on data generated by humans, we may not expect the artificial model to outperform the humans on their original objectives. In this work, we study the phenomenon of transcendence: when a generative model achieves capabilities that surpass the abilities of the experts generating its data. We demonstrate transcendence by training an autoregressive transformer to play chess from game transcripts, and show that the trained model can sometimes achieve better performance than all players in the dataset. We theoretically prove that transcendence is enabled by low-temperature sampling, and rigorously assess this experimentally. Finally, we discuss other sources of transcendence, laying the groundwork for future investigation of this phenomenon in a broader setting.

The Evolution of Statistical Induction Heads: In-Context Learning Markov Chains

Large language models have the ability to generate text that mimics patterns in their inputs. We introduce a simple Markov Chain sequence modeling task in order to study how this in-context learning (ICL) capability emerges. In our setting, each example is sampled from a Markov chain drawn from a prior distribution over Markov chains. Transformers trained on this task form \emph{statistical induction heads} which compute accurate next-token probabilities given the bigram statistics of the context. During the course of training, models pass through multiple phases: after an initial stage in which predictions are uniform, they learn to sub-optimally predict using in-context single-token statistics (unigrams); then, there is a rapid phase transition to the correct in-context bigram solution. We conduct an empirical and theoretical investigation of this multi-phase process, showing how successful learning results from the interaction between the transformer's layers, and uncovering evidence that the presence of the simpler unigram solution may delay formation of the final bigram solution. We examine how learning is affected by varying the prior distribution over Markov chains, and consider the generalization of our in-context learning of Markov chains (ICL-MC) task to $n$-grams for $n > 2$.

Repeat After Me: Transformers are Better than State Space Models at Copying

Transformers are the dominant architecture for sequence modeling, but there is growing interest in models that use a fixed-size latent state that does not depend on the sequence length, which we refer to as "generalized state space models" (GSSMs). In this paper we show that while GSSMs are promising in terms of inference-time efficiency, they are limited compared to transformer models on tasks that require copying from the input context. We start with a theoretical analysis of the simple task of string copying and prove that a two layer transformer can copy strings of exponential length while GSSMs are fundamentally limited by their fixed-size latent state. Empirically, we find that transformers outperform GSSMs in terms of efficiency and generalization on synthetic tasks that require copying the context. Finally, we evaluate pretrained large language models and find that transformer models dramatically outperform state space models at copying and retrieving information from context. Taken together, these results suggest a fundamental gap between transformers and GSSMs on tasks of practical interest.

Auto-Regressive Next-Token Predictors are Universal Learners

Large language models display remarkable capabilities in logical and mathematical reasoning, allowing them to solve complex tasks. Interestingly, these abilities emerge in networks trained on the simple task of next-token prediction. In this work, we present a theoretical framework for studying auto-regressive next-token predictors. We demonstrate that even simple models such as linear next-token predictors, trained on Chain-of-Thought (CoT) data, can approximate any function efficiently computed by a Turing machine. We introduce a new complexity measure -- length complexity -- which measures the number of intermediate tokens in a CoT sequence required to approximate some target function, and analyze the interplay between length complexity and other notions of complexity. Finally, we show experimentally that simple next-token predictors, such as linear networks and shallow Multi-Layer Perceptrons (MLPs), display non-trivial performance on text generation and arithmetic tasks. Our results demonstrate that the power of language models can be attributed, to a great extent, to the auto-regressive next-token training scheme, and not necessarily to a particular choice of architecture.

Pareto Frontiers in Neural Feature Learning: Data, Compute, Width, and Luck

This work investigates the nuanced algorithm design choices for deep learning in the presence of computational-statistical gaps. We begin by considering offline sparse parity learning, a supervised classification problem which admits a statistical query lower bound for gradient-based training of a multilayer perceptron. This lower bound can be interpreted as a multi-resource tradeoff frontier: successful learning can only occur if one is sufficiently rich (large model), knowledgeable (large dataset), patient (many training iterations), or lucky (many random guesses). We show, theoretically and experimentally, that sparse initialization and increasing network width yield significant improvements in sample efficiency in this setting. Here, width plays the role of parallel search: it amplifies the probability of finding "lottery ticket" neurons, which learn sparse features more sample-efficiently. Finally, we show that the synthetic sparse parity task can be useful as a proxy for real problems requiring axis-aligned feature learning. We demonstrate improved sample efficiency on tabular classification benchmarks by using wide, sparsely-initialized MLP models; these networks sometimes outperform tuned random forests.

Corgi^2: A Hybrid Offline-Online Approach To Storage-Aware Data Shuffling For SGD

When using Stochastic Gradient Descent (SGD) for training machine learning models, it is often crucial to provide the model with examples sampled at random from the dataset. However, for large datasets stored in the cloud, random access to individual examples is often costly and inefficient. A recent work \cite{corgi}, proposed an online shuffling algorithm called CorgiPile, which greatly improves efficiency of data access, at the cost some performance loss, which is particularly apparent for large datasets stored in homogeneous shards (e.g., video datasets). In this paper, we introduce a novel two-step partial data shuffling strategy for SGD which combines an offline iteration of the CorgiPile method with a subsequent online iteration. Our approach enjoys the best of both worlds: it performs similarly to SGD with random access (even for homogenous data) without compromising the data access efficiency of CorgiPile. We provide a comprehensive theoretical analysis of the convergence properties of our method and demonstrate its practical advantages through experimental results.

SubTuning: Efficient Finetuning for Multi-Task Learning

Finetuning a pretrained model has become a standard approach for training neural networks on novel tasks, resulting in fast convergence and improved performance. In this work, we study an alternative finetuning method, where instead of finetuning all the weights of the network, we only train a carefully chosen subset of layers, keeping the rest of the weights frozen at their initial (pretrained) values. We demonstrate that \emph{subset finetuning} (or SubTuning) often achieves accuracy comparable to full finetuning of the model, and even surpasses the performance of full finetuning when training data is scarce. Therefore, SubTuning allows deploying new tasks at minimal computational cost, while enjoying the benefits of finetuning the entire model. This yields a simple and effective method for multi-task learning, where different tasks do not interfere with one another, and yet share most of the resources at inference time. We demonstrate the efficiency of SubTuning across multiple tasks, using different network architectures and pretraining methods.