Universal Length Generalization with Turing Programs

Length generalization refers to the ability to extrapolate from short training sequences to long test sequences and is a challenge for current large language models. While prior work has proposed some architecture or data format changes to achieve length generalization, these proposals typically apply to a limited set of tasks. Building on prior scratchpad and Chain-of-Thought (CoT) techniques, we propose Turing Programs, a novel CoT strategy that decomposes an algorithmic task into steps mimicking the computation of a Turing Machine. This framework is both universal, as it can accommodate any algorithmic task, and simple, requiring only copying text from the context with small modifications. We show that by using Turing Programs, we obtain robust length generalization on a range of algorithmic tasks: addition, multiplication and in-context SGD. We then demonstrate that transformers achieve length generalization on random Turing Programs, suggesting that length generalization is possible for any algorithmic task. Finally, we theoretically prove that transformers can implement Turing Programs, constructing a simple RASP (Weiss et al.) program that simulates an arbitrary Turing machine.

Learning quantum symmetries with interactive quantum-classical variational algorithms

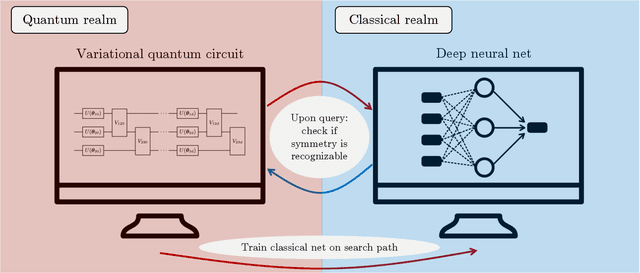
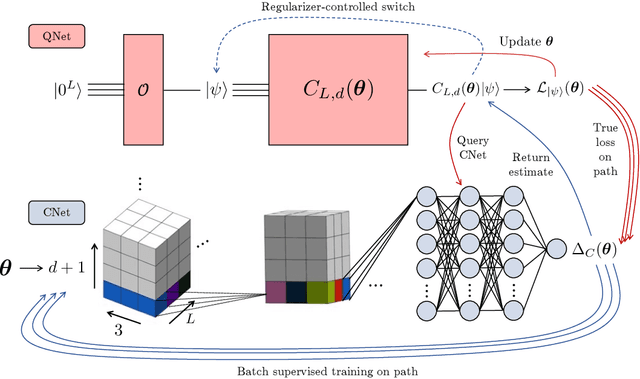
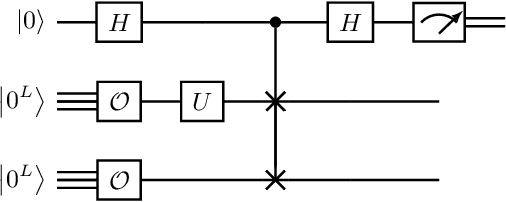
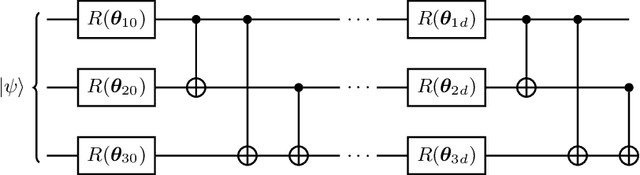
A symmetry of a state $\lvert \psi \rangle$ is a unitary operator of which $\lvert \psi \rangle$ is an eigenvector. When $\lvert \psi \rangle$ is an unknown state supplied by a black-box oracle, the state's symmetries serve to characterize it, and often relegate much of the desired information about $\lvert \psi \rangle$. In this paper, we develop a variational hybrid quantum-classical learning scheme to systematically probe for symmetries of $\lvert \psi \rangle$ with no a priori assumptions about the state. This procedure can be used to learn various symmetries at the same time. In order to avoid re-learning already known symmetries, we introduce an interactive protocol with a classical deep neural net. The classical net thereby regularizes against repetitive findings and allows our algorithm to terminate empirically with all possible symmetries found. Our scheme can be implemented efficiently on average with non-local SWAP gates; we also give a less efficient algorithm with only local operations, which may be more appropriate for current noisy quantum devices. We demonstrate our algorithm on representative families of states.