Understanding Overparametrization in Survival Models through Interpolation

Classical statistical learning theory predicts a U-shaped relationship between test loss and model capacity, driven by the bias-variance trade-off. Recent advances in modern machine learning have revealed a more complex pattern, \textit{double-descent}, in which test loss, after peaking near the interpolation threshold, decreases again as model capacity continues to grow. While this behavior has been extensively analyzed in regression and classification, its manifestation in survival analysis remains unexplored. This study investigates overparametrization in four representative survival models: DeepSurv, PC-Hazard, Nnet-Survival, and N-MTLR. We rigorously define \textit{interpolation} and \textit{finite-norm interpolation}, two key characteristics of loss-based models to understand \textit{double-descent}. We then show the existence (or absence) of \textit{(finite-norm) interpolation} of all four models. Our findings clarify how likelihood-based losses and model implementation jointly determine the feasibility of \textit{interpolation} and show that overparametrization should not be regarded as benign for survival models. All theoretical results are supported by numerical experiments that highlight the distinct generalization behaviors of survival models.

How to Find Fantastic Papers: Self-Rankings as a Powerful Predictor of Scientific Impact Beyond Peer Review

Peer review in academic research aims not only to ensure factual correctness but also to identify work of high scientific potential that can shape future research directions. This task is especially critical in fast-moving fields such as artificial intelligence (AI), yet it has become increasingly difficult given the rapid growth of submissions. In this paper, we investigate an underexplored measure for identifying high-impact research: authors' own rankings of their multiple submissions to the same AI conference. Grounded in game-theoretic reasoning, we hypothesize that self-rankings are informative because authors possess unique understanding of their work's conceptual depth and long-term promise. To test this hypothesis, we conducted a large-scale experiment at a leading AI conference, where 1,342 researchers self-ranked their 2,592 submissions by perceived quality. Tracking outcomes over more than a year, we found that papers ranked highest by their authors received twice as many citations as their lowest-ranked counterparts; self-rankings were especially effective at identifying highly cited papers (those with over 150 citations). Moreover, we showed that self-rankings outperformed peer review scores in predicting future citation counts. Our results remained robust after accounting for confounders such as preprint posting time and self-citations. Together, these findings demonstrate that authors' self-rankings provide a reliable and valuable complement to peer review for identifying and elevating high-impact research in AI.

Lower Ricci Curvature for Hypergraphs

Networks with higher-order interactions, prevalent in biological, social, and information systems, are naturally represented as hypergraphs, yet their structural complexity poses fundamental challenges for geometric characterization. While curvature-based methods offer powerful insights in graph analysis, existing extensions to hypergraphs suffer from critical trade-offs: combinatorial approaches such as Forman-Ricci curvature capture only coarse features, whereas geometric methods like Ollivier-Ricci curvature offer richer expressivity but demand costly optimal transport computations. To address these challenges, we introduce hypergraph lower Ricci curvature (HLRC), a novel curvature metric defined in closed form that achieves a principled balance between interpretability and efficiency. Evaluated across diverse synthetic and real-world hypergraph datasets, HLRC consistently reveals meaningful higher-order organization, distinguishing intra- from inter-community hyperedges, uncovering latent semantic labels, tracking temporal dynamics, and supporting robust clustering of hypergraphs based on global structure. By unifying geometric sensitivity with algorithmic simplicity, HLRC provides a versatile foundation for hypergraph analytics, with broad implications for tasks including node classification, anomaly detection, and generative modeling in complex systems.

HR-VILAGE-3K3M: A Human Respiratory Viral Immunization Longitudinal Gene Expression Dataset for Systems Immunity

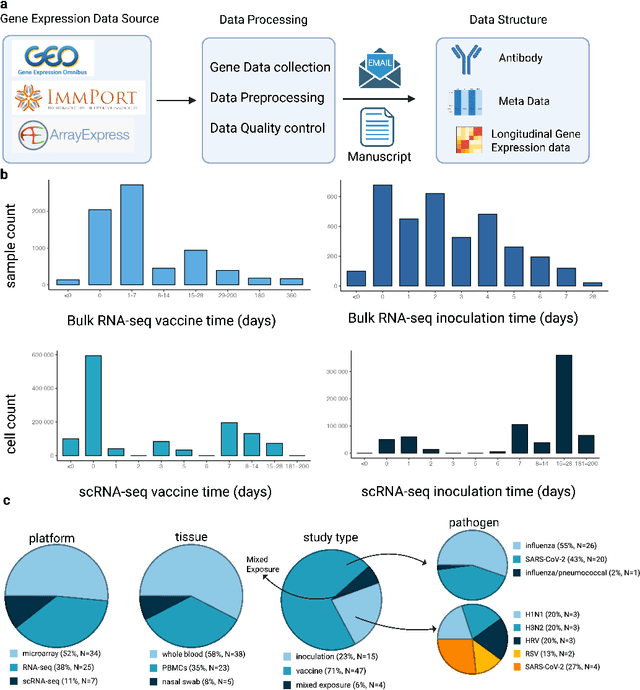
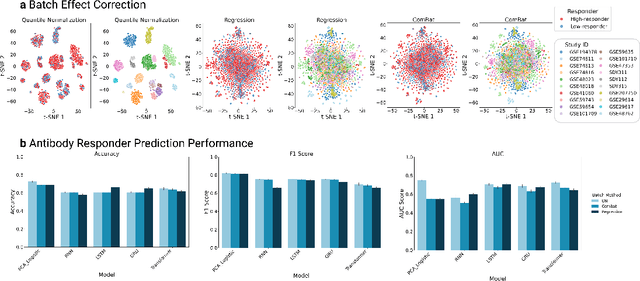
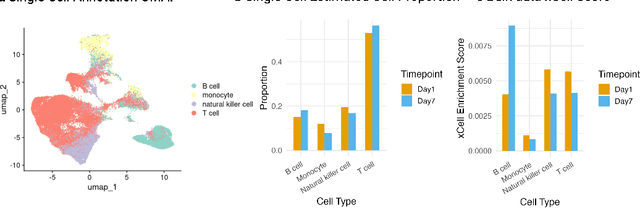
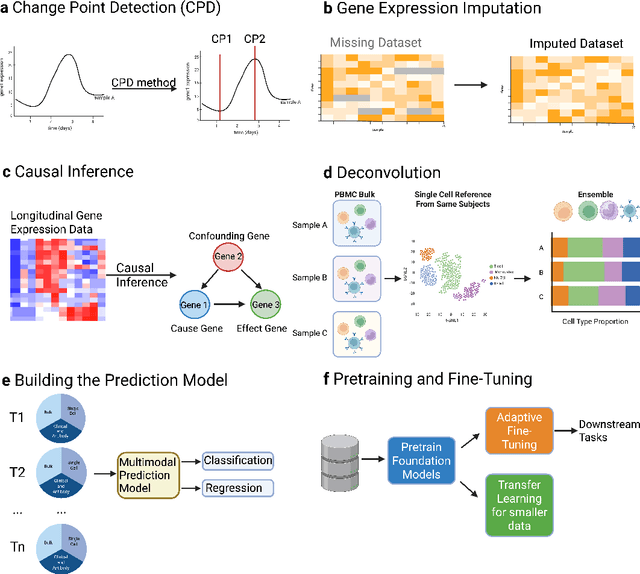
Respiratory viral infections pose a global health burden, yet the cellular immune responses driving protection or pathology remain unclear. Natural infection cohorts often lack pre-exposure baseline data and structured temporal sampling. In contrast, inoculation and vaccination trials generate insightful longitudinal transcriptomic data. However, the scattering of these datasets across platforms, along with inconsistent metadata and preprocessing procedure, hinders AI-driven discovery. To address these challenges, we developed the Human Respiratory Viral Immunization LongitudinAl Gene Expression (HR-VILAGE-3K3M) repository: an AI-ready, rigorously curated dataset that integrates 14,136 RNA-seq profiles from 3,178 subjects across 66 studies encompassing over 2.56 million cells. Spanning vaccination, inoculation, and mixed exposures, the dataset includes microarray, bulk RNA-seq, and single-cell RNA-seq from whole blood, PBMCs, and nasal swabs, sourced from GEO, ImmPort, and ArrayExpress. We harmonized subject-level metadata, standardized outcome measures, applied unified preprocessing pipelines with rigorous quality control, and aligned all data to official gene symbols. To demonstrate the utility of HR-VILAGE-3K3M, we performed predictive modeling of vaccine responders and evaluated batch-effect correction methods. Beyond these initial demonstrations, it supports diverse systems immunology applications and benchmarking of feature selection and transfer learning algorithms. Its scale and heterogeneity also make it ideal for pretraining foundation models of the human immune response and for advancing multimodal learning frameworks. As the largest longitudinal transcriptomic resource for human respiratory viral immunization, it provides an accessible platform for reproducible AI-driven research, accelerating systems immunology and vaccine development against emerging viral threats.

Deep Generative Models: Complexity, Dimensionality, and Approximation

Generative networks have shown remarkable success in learning complex data distributions, particularly in generating high-dimensional data from lower-dimensional inputs. While this capability is well-documented empirically, its theoretical underpinning remains unclear. One common theoretical explanation appeals to the widely accepted manifold hypothesis, which suggests that many real-world datasets, such as images and signals, often possess intrinsic low-dimensional geometric structures. Under this manifold hypothesis, it is widely believed that to approximate a distribution on a $d$-dimensional Riemannian manifold, the latent dimension needs to be at least $d$ or $d+1$. In this work, we show that this requirement on the latent dimension is not necessary by demonstrating that generative networks can approximate distributions on $d$-dimensional Riemannian manifolds from inputs of any arbitrary dimension, even lower than $d$, taking inspiration from the concept of space-filling curves. This approach, in turn, leads to a super-exponential complexity bound of the deep neural networks through expanded neurons. Our findings thus challenge the conventional belief on the relationship between input dimensionality and the ability of generative networks to model data distributions. This novel insight not only corroborates the practical effectiveness of generative networks in handling complex data structures, but also underscores a critical trade-off between approximation error, dimensionality, and model complexity.

A Novel Compact LLM Framework for Local, High-Privacy EHR Data Applications

Large Language Models (LLMs) have shown impressive capabilities in natural language processing, yet their use in sensitive domains like healthcare, particularly with Electronic Health Records (EHR), faces significant challenges due to privacy concerns and limited computational resources. This paper presents a compact LLM framework designed for local deployment in settings with strict privacy requirements and limited access to high-performance GPUs. We introduce a novel preprocessing technique that uses information extraction methods, e.g., regular expressions, to filter and emphasize critical information in clinical notes, enhancing the performance of smaller LLMs on EHR data. Our framework is evaluated using zero-shot and few-shot learning paradigms on both private and publicly available (MIMIC-IV) datasets, and we also compare its performance with fine-tuned LLMs on the MIMIC-IV dataset. The results demonstrate that our preprocessing approach significantly boosts the prediction accuracy of smaller LLMs, making them suitable for high-privacy, resource-constrained applications. This study offers valuable insights into optimizing LLM performance for sensitive, data-intensive tasks while addressing computational and privacy limitations.

Analysis of the ICML 2023 Ranking Data: Can Authors' Opinions of Their Own Papers Assist Peer Review in Machine Learning?

We conducted an experiment during the review process of the 2023 International Conference on Machine Learning (ICML) that requested authors with multiple submissions to rank their own papers based on perceived quality. We received 1,342 rankings, each from a distinct author, pertaining to 2,592 submissions. In this paper, we present an empirical analysis of how author-provided rankings could be leveraged to improve peer review processes at machine learning conferences. We focus on the Isotonic Mechanism, which calibrates raw review scores using author-provided rankings. Our analysis demonstrates that the ranking-calibrated scores outperform raw scores in estimating the ground truth ``expected review scores'' in both squared and absolute error metrics. Moreover, we propose several cautious, low-risk approaches to using the Isotonic Mechanism and author-provided rankings in peer review processes, including assisting senior area chairs' oversight of area chairs' recommendations, supporting the selection of paper awards, and guiding the recruitment of emergency reviewers. We conclude the paper by addressing the study's limitations and proposing future research directions.

STimage-1K4M: A histopathology image-gene expression dataset for spatial transcriptomics

Recent advances in multi-modal algorithms have driven and been driven by the increasing availability of large image-text datasets, leading to significant strides in various fields, including computational pathology. However, in most existing medical image-text datasets, the text typically provides high-level summaries that may not sufficiently describe sub-tile regions within a large pathology image. For example, an image might cover an extensive tissue area containing cancerous and healthy regions, but the accompanying text might only specify that this image is a cancer slide, lacking the nuanced details needed for in-depth analysis. In this study, we introduce STimage-1K4M, a novel dataset designed to bridge this gap by providing genomic features for sub-tile images. STimage-1K4M contains 1,149 images derived from spatial transcriptomics data, which captures gene expression information at the level of individual spatial spots within a pathology image. Specifically, each image in the dataset is broken down into smaller sub-image tiles, with each tile paired with 15,000-30,000 dimensional gene expressions. With 4,293,195 pairs of sub-tile images and gene expressions, STimage-1K4M offers unprecedented granularity, paving the way for a wide range of advanced research in multi-modal data analysis an innovative applications in computational pathology, and beyond.

On the Identifiability and Interpretability of Gaussian Process Models

In this paper, we critically examine the prevalent practice of using additive mixtures of Mat\'ern kernels in single-output Gaussian process (GP) models and explore the properties of multiplicative mixtures of Mat\'ern kernels for multi-output GP models. For the single-output case, we derive a series of theoretical results showing that the smoothness of a mixture of Mat\'ern kernels is determined by the least smooth component and that a GP with such a kernel is effectively equivalent to the least smooth kernel component. Furthermore, we demonstrate that none of the mixing weights or parameters within individual kernel components are identifiable. We then turn our attention to multi-output GP models and analyze the identifiability of the covariance matrix $A$ in the multiplicative kernel $K(x,y) = AK_0(x,y)$, where $K_0$ is a standard single output kernel such as Mat\'ern. We show that $A$ is identifiable up to a multiplicative constant, suggesting that multiplicative mixtures are well suited for multi-output tasks. Our findings are supported by extensive simulations and real applications for both single- and multi-output settings. This work provides insight into kernel selection and interpretation for GP models, emphasizing the importance of choosing appropriate kernel structures for different tasks.

Contrastive inverse regression for dimension reduction

Supervised dimension reduction (SDR) has been a topic of growing interest in data science, as it enables the reduction of high-dimensional covariates while preserving the functional relation with certain response variables of interest. However, existing SDR methods are not suitable for analyzing datasets collected from case-control studies. In this setting, the goal is to learn and exploit the low-dimensional structure unique to or enriched by the case group, also known as the foreground group. While some unsupervised techniques such as the contrastive latent variable model and its variants have been developed for this purpose, they fail to preserve the functional relationship between the dimension-reduced covariates and the response variable. In this paper, we propose a supervised dimension reduction method called contrastive inverse regression (CIR) specifically designed for the contrastive setting. CIR introduces an optimization problem defined on the Stiefel manifold with a non-standard loss function. We prove the convergence of CIR to a local optimum using a gradient descent-based algorithm, and our numerical study empirically demonstrates the improved performance over competing methods for high-dimensional data.