PERRY: Policy Evaluation with Confidence Intervals using Auxiliary Data

Off-policy evaluation (OPE) methods aim to estimate the value of a new reinforcement learning (RL) policy prior to deployment. Recent advances have shown that leveraging auxiliary datasets, such as those synthesized by generative models, can improve the accuracy of these value estimates. Unfortunately, such auxiliary datasets may also be biased, and existing methods for using data augmentation for OPE in RL lack principled uncertainty quantification. In high stakes settings like healthcare, reliable uncertainty estimates are important for comparing policy value estimates. In this work, we propose two approaches to construct valid confidence intervals for OPE when using data augmentation. The first provides a confidence interval over the policy performance conditioned on a particular initial state $V^{\pi}(s_0)$-- such intervals are particularly important for human-centered applications. To do so we introduce a new conformal prediction method for high dimensional state MDPs. Second, we consider the more common task of estimating the average policy performance over many initial states; to do so we draw on ideas from doubly robust estimation and prediction powered inference. Across simulators spanning robotics, healthcare and inventory management, and a real healthcare dataset from MIMIC-IV, we find that our methods can use augmented data and still consistently produce intervals that cover the ground truth values, unlike previously proposed methods.

Sharpe Ratio-Guided Active Learning for Preference Optimization in RLHF

Reinforcement learning from human feedback (RLHF) has become a cornerstone of the training and alignment pipeline for large language models (LLMs). Recent advances, such as direct preference optimization (DPO), have simplified the preference learning step. However, collecting preference data remains a challenging and costly process, often requiring expert annotation. This cost can be mitigated by carefully selecting the data points presented for annotation. In this work, we propose an active learning approach to efficiently select prompt and preference pairs using a risk assessment strategy based on the Sharpe Ratio. To address the challenge of unknown preferences prior to annotation, our method evaluates the gradients of all potential preference annotations to assess their impact on model updates. These gradient-based evaluations enable risk assessment of data points regardless of the annotation outcome. By leveraging the DPO loss derivations, we derive a closed-form expression for computing these Sharpe ratios on a per-tuple basis, ensuring our approach remains both tractable and computationally efficient. We also introduce two variants of our method, each making different assumptions about prior information. Experimental results demonstrate that our method outperforms the baseline by up to 5% in win rates against the chosen completion with limited human preference data across several language models and real-world datasets.

CANDOR: Counterfactual ANnotated DOubly Robust Off-Policy Evaluation

Off-policy evaluation (OPE) provides safety guarantees by estimating the performance of a policy before deployment. Recent work introduced IS+, an importance sampling (IS) estimator that uses expert-annotated counterfactual samples to improve behavior dataset coverage. However, IS estimators are known to have high variance; furthermore, the performance of IS+ deteriorates when annotations are imperfect. In this work, we propose a family of OPE estimators inspired by the doubly robust (DR) principle. A DR estimator combines IS with a reward model estimate, known as the direct method (DM), and offers favorable statistical guarantees. We propose three strategies for incorporating counterfactual annotations into a DR-inspired estimator and analyze their properties under various realistic settings. We prove that using imperfect annotations in the DM part of the estimator best leverages the annotations, as opposed to using them in the IS part. To support our theoretical findings, we evaluate the proposed estimators in three contextual bandit environments. Our empirical results show that when the reward model is misspecified and the annotations are imperfect, it is most beneficial to use the annotations only in the DM portion of a DR estimator. Based on these theoretical and empirical insights, we provide a practical guide for using counterfactual annotations in different realistic settings.

Adaptive Interventions with User-Defined Goals for Health Behavior Change

Physical inactivity remains a major public health concern, having associations with adverse health outcomes such as cardiovascular disease and type-2 diabetes. Mobile health applications present a promising avenue for low-cost, scalable physical activity promotion, yet often suffer from small effect sizes and low adherence rates, particularly in comparison to human coaching. Goal-setting is a critical component of health coaching that has been underutilized in adaptive algorithms for mobile health interventions. This paper introduces a modification to the Thompson sampling algorithm that places emphasis on individualized goal-setting by optimizing personalized reward functions. As a step towards supporting goal-setting, this paper offers a balanced approach that can leverage shared structure while optimizing individual preferences and goals. We prove that our modification incurs only a constant penalty on the cumulative regret while preserving the sample complexity benefits of data sharing. In a physical activity simulator, we demonstrate that our algorithm achieves substantial improvements in cumulative regret compared to baselines that do not share data or do not optimize for individualized rewards.

Bayesian Non-linear Latent Variable Modeling via Random Fourier Features

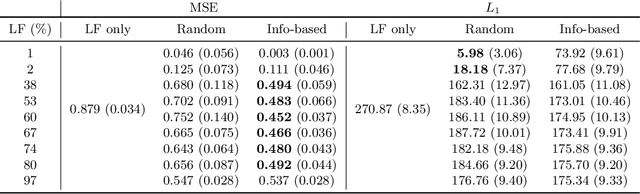
The Gaussian process latent variable model (GPLVM) is a popular probabilistic method used for nonlinear dimension reduction, matrix factorization, and state-space modeling. Inference for GPLVMs is computationally tractable only when the data likelihood is Gaussian. Moreover, inference for GPLVMs has typically been restricted to obtaining maximum a posteriori point estimates, which can lead to overfitting, or variational approximations, which mischaracterize the posterior uncertainty. Here, we present a method to perform Markov chain Monte Carlo (MCMC) inference for generalized Bayesian nonlinear latent variable modeling. The crucial insight necessary to generalize GPLVMs to arbitrary observation models is that we approximate the kernel function in the Gaussian process mappings with random Fourier features; this allows us to compute the gradient of the posterior in closed form with respect to the latent variables. We show that we can generalize GPLVMs to non-Gaussian observations, such as Poisson, negative binomial, and multinomial distributions, using our random feature latent variable model (RFLVM). Our generalized RFLVMs perform on par with state-of-the-art latent variable models on a wide range of applications, including motion capture, images, and text data for the purpose of estimating the latent structure and imputing the missing data of these complex data sets.

Kernel Density Bayesian Inverse Reinforcement Learning

Inverse reinforcement learning~(IRL) is a powerful framework to infer an agent's reward function by observing its behavior, but IRL algorithms that learn point estimates of the reward function can be misleading because there may be several functions that describe an agent's behavior equally well. A Bayesian approach to IRL models a distribution over candidate reward functions, alleviating the shortcomings of learning a point estimate. However, several Bayesian IRL algorithms use a $Q$-value function in place of the likelihood function. The resulting posterior is computationally intensive to calculate, has few theoretical guarantees, and the $Q$-value function is often a poor approximation for the likelihood. We introduce kernel density Bayesian IRL (KD-BIRL), which uses conditional kernel density estimation to directly approximate the likelihood, providing an efficient framework that, with a modified reward function parameterization, is applicable to environments with complex and infinite state spaces. We demonstrate KD-BIRL's benefits through a series of experiments in Gridworld environments and a simulated sepsis treatment task.

Variance Minimization in the Wasserstein Space for Invariant Causal Prediction

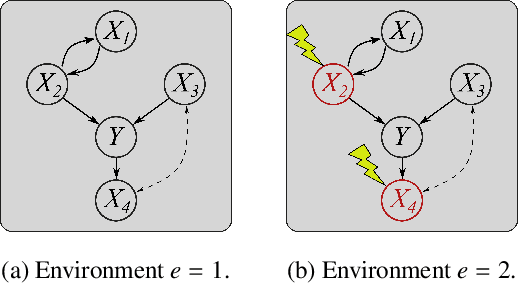
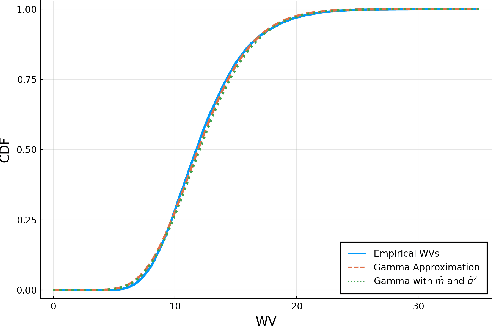
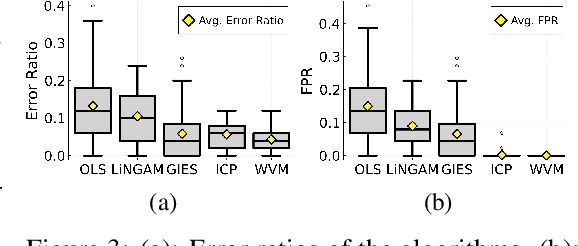
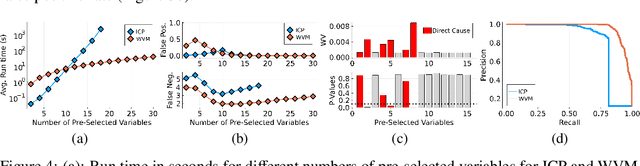
Selecting powerful predictors for an outcome is a cornerstone task for machine learning. However, some types of questions can only be answered by identifying the predictors that causally affect the outcome. A recent approach to this causal inference problem leverages the invariance property of a causal mechanism across differing experimental environments (Peters et al., 2016; Heinze-Deml et al., 2018). This method, invariant causal prediction (ICP), has a substantial computational defect -- the runtime scales exponentially with the number of possible causal variables. In this work, we show that the approach taken in ICP may be reformulated as a series of nonparametric tests that scales linearly in the number of predictors. Each of these tests relies on the minimization of a novel loss function -- the Wasserstein variance -- that is derived from tools in optimal transport theory and is used to quantify distributional variability across environments. We prove under mild assumptions that our method is able to recover the set of identifiable direct causes, and we demonstrate in our experiments that it is competitive with other benchmark causal discovery algorithms.

Nonnegative spatial factorization

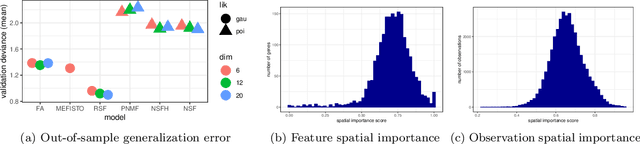
Gaussian processes are widely used for the analysis of spatial data due to their nonparametric flexibility and ability to quantify uncertainty, and recently developed scalable approximations have facilitated application to massive datasets. For multivariate outcomes, linear models of coregionalization combine dimension reduction with spatial correlation. However, their real-valued latent factors and loadings are difficult to interpret because, unlike nonnegative models, they do not recover a parts-based representation. We present nonnegative spatial factorization (NSF), a spatially-aware probabilistic dimension reduction model that naturally encourages sparsity. We compare NSF to real-valued spatial factorizations such as MEFISTO and nonspatial dimension reduction methods using simulations and high-dimensional spatial transcriptomics data. NSF identifies generalizable spatial patterns of gene expression. Since not all patterns of gene expression are spatial, we also propose a hybrid extension of NSF that combines spatial and nonspatial components, enabling quantification of spatial importance for both observations and features. A TensorFlow implementation of NSF is available from https://github.com/willtownes/nsf-paper .

Active multi-fidelity Bayesian online changepoint detection

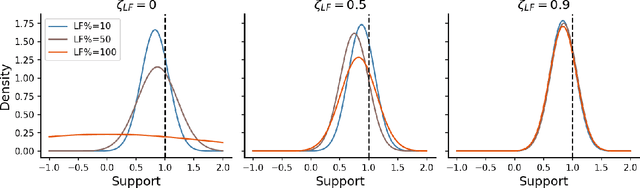
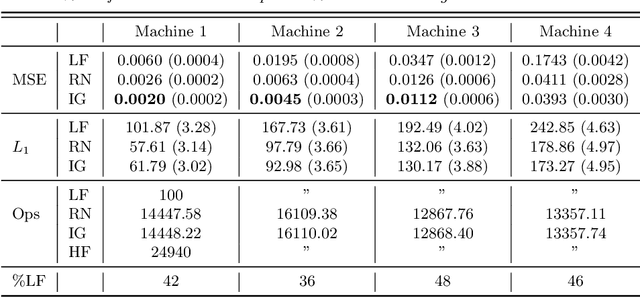
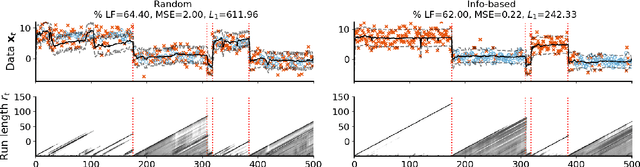
Online algorithms for detecting changepoints, or abrupt shifts in the behavior of a time series, are often deployed with limited resources, e.g., to edge computing settings such as mobile phones or industrial sensors. In these scenarios it may be beneficial to trade the cost of collecting an environmental measurement against the quality or "fidelity" of this measurement and how the measurement affects changepoint estimation. For instance, one might decide between inertial measurements or GPS to determine changepoints for motion. A Bayesian approach to changepoint detection is particularly appealing because we can represent our posterior uncertainty about changepoints and make active, cost-sensitive decisions about data fidelity to reduce this posterior uncertainty. Moreover, the total cost could be dramatically lowered through active fidelity switching, while remaining robust to changes in data distribution. We propose a multi-fidelity approach that makes cost-sensitive decisions about which data fidelity to collect based on maximizing information gain with respect to changepoints. We evaluate this framework on synthetic, video, and audio data and show that this information-based approach results in accurate predictions while reducing total cost.

Latent variable modeling with random features

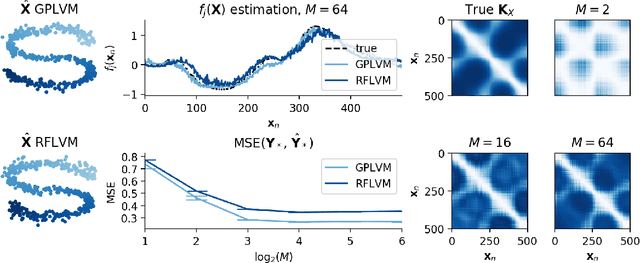
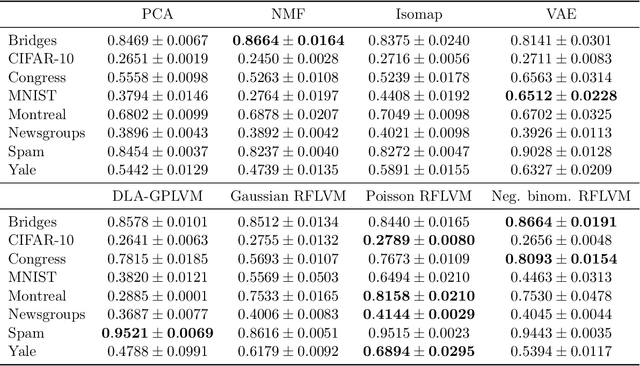
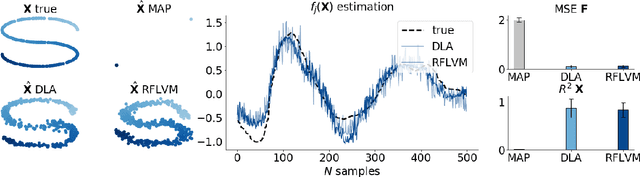
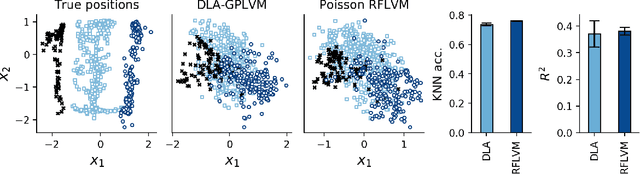
Gaussian process-based latent variable models are flexible and theoretically grounded tools for nonlinear dimension reduction, but generalizing to non-Gaussian data likelihoods within this nonlinear framework is statistically challenging. Here, we use random features to develop a family of nonlinear dimension reduction models that are easily extensible to non-Gaussian data likelihoods; we call these random feature latent variable models (RFLVMs). By approximating a nonlinear relationship between the latent space and the observations with a function that is linear with respect to random features, we induce closed-form gradients of the posterior distribution with respect to the latent variable. This allows the RFLVM framework to support computationally tractable nonlinear latent variable models for a variety of data likelihoods in the exponential family without specialized derivations. Our generalized RFLVMs produce results comparable with other state-of-the-art dimension reduction methods on diverse types of data, including neural spike train recordings, images, and text data.