EigenVI: score-based variational inference with orthogonal function expansions

We develop EigenVI, an eigenvalue-based approach for black-box variational inference (BBVI). EigenVI constructs its variational approximations from orthogonal function expansions. For distributions over $\mathbb{R}^D$, the lowest order term in these expansions provides a Gaussian variational approximation, while higher-order terms provide a systematic way to model non-Gaussianity. These approximations are flexible enough to model complex distributions (multimodal, asymmetric), but they are simple enough that one can calculate their low-order moments and draw samples from them. EigenVI can also model other types of random variables (e.g., nonnegative, bounded) by constructing variational approximations from different families of orthogonal functions. Within these families, EigenVI computes the variational approximation that best matches the score function of the target distribution by minimizing a stochastic estimate of the Fisher divergence. Notably, this optimization reduces to solving a minimum eigenvalue problem, so that EigenVI effectively sidesteps the iterative gradient-based optimizations that are required for many other BBVI algorithms. (Gradient-based methods can be sensitive to learning rates, termination criteria, and other tunable hyperparameters.) We use EigenVI to approximate a variety of target distributions, including a benchmark suite of Bayesian models from posteriordb. On these distributions, we find that EigenVI is more accurate than existing methods for Gaussian BBVI.

Batch, match, and patch: low-rank approximations for score-based variational inference

Black-box variational inference (BBVI) scales poorly to high dimensional problems when it is used to estimate a multivariate Gaussian approximation with a full covariance matrix. In this paper, we extend the batch-and-match (BaM) framework for score-based BBVI to problems where it is prohibitively expensive to store such covariance matrices, let alone to estimate them. Unlike classical algorithms for BBVI, which use gradient descent to minimize the reverse Kullback-Leibler divergence, BaM uses more specialized updates to match the scores of the target density and its Gaussian approximation. We extend the updates for BaM by integrating them with a more compact parameterization of full covariance matrices. In particular, borrowing ideas from factor analysis, we add an extra step to each iteration of BaM -- a patch -- that projects each newly updated covariance matrix into a more efficiently parameterized family of diagonal plus low rank matrices. We evaluate this approach on a variety of synthetic target distributions and real-world problems in high-dimensional inference.

Batch and match: black-box variational inference with a score-based divergence

Most leading implementations of black-box variational inference (BBVI) are based on optimizing a stochastic evidence lower bound (ELBO). But such approaches to BBVI often converge slowly due to the high variance of their gradient estimates. In this work, we propose batch and match (BaM), an alternative approach to BBVI based on a score-based divergence. Notably, this score-based divergence can be optimized by a closed-form proximal update for Gaussian variational families with full covariance matrices. We analyze the convergence of BaM when the target distribution is Gaussian, and we prove that in the limit of infinite batch size the variational parameter updates converge exponentially quickly to the target mean and covariance. We also evaluate the performance of BaM on Gaussian and non-Gaussian target distributions that arise from posterior inference in hierarchical and deep generative models. In these experiments, we find that BaM typically converges in fewer (and sometimes significantly fewer) gradient evaluations than leading implementations of BBVI based on ELBO maximization.

Kernel Density Bayesian Inverse Reinforcement Learning

Inverse reinforcement learning~(IRL) is a powerful framework to infer an agent's reward function by observing its behavior, but IRL algorithms that learn point estimates of the reward function can be misleading because there may be several functions that describe an agent's behavior equally well. A Bayesian approach to IRL models a distribution over candidate reward functions, alleviating the shortcomings of learning a point estimate. However, several Bayesian IRL algorithms use a $Q$-value function in place of the likelihood function. The resulting posterior is computationally intensive to calculate, has few theoretical guarantees, and the $Q$-value function is often a poor approximation for the likelihood. We introduce kernel density Bayesian IRL (KD-BIRL), which uses conditional kernel density estimation to directly approximate the likelihood, providing an efficient framework that, with a modified reward function parameterization, is applicable to environments with complex and infinite state spaces. We demonstrate KD-BIRL's benefits through a series of experiments in Gridworld environments and a simulated sepsis treatment task.

Multi-fidelity Monte Carlo: a pseudo-marginal approach

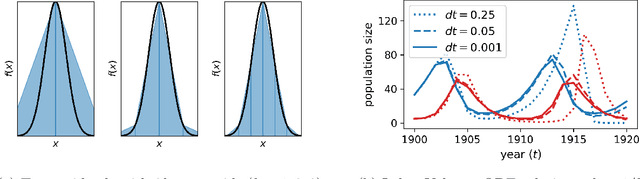
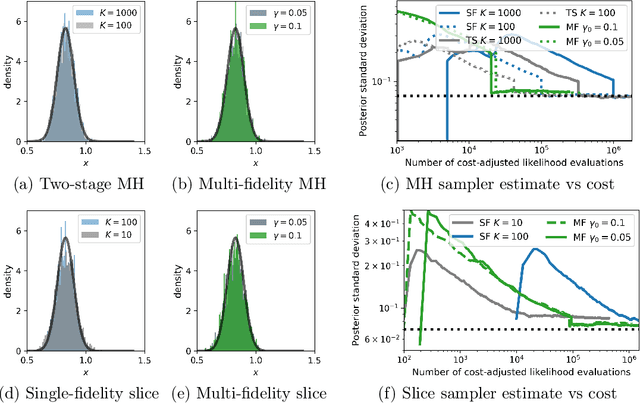
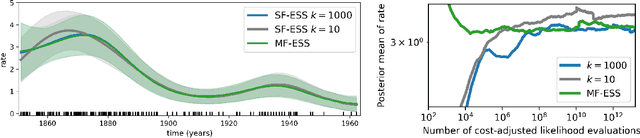
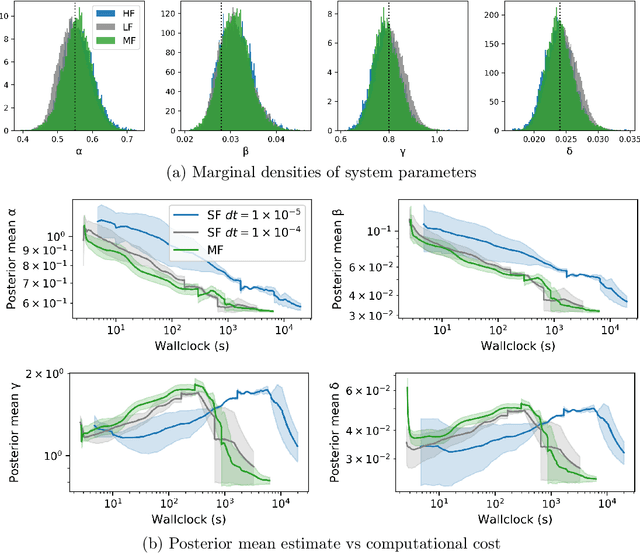
Markov chain Monte Carlo (MCMC) is an established approach for uncertainty quantification and propagation in scientific applications. A key challenge in applying MCMC to scientific domains is computation: the target density of interest is often a function of expensive computations, such as a high-fidelity physical simulation, an intractable integral, or a slowly-converging iterative algorithm. Thus, using an MCMC algorithms with an expensive target density becomes impractical, as these expensive computations need to be evaluated at each iteration of the algorithm. In practice, these computations often approximated via a cheaper, low-fidelity computation, leading to bias in the resulting target density. Multi-fidelity MCMC algorithms combine models of varying fidelities in order to obtain an approximate target density with lower computational cost. In this paper, we describe a class of asymptotically exact multi-fidelity MCMC algorithms for the setting where a sequence of models of increasing fidelity can be computed that approximates the expensive target density of interest. We take a pseudo-marginal MCMC approach for multi-fidelity inference that utilizes a cheaper, randomized-fidelity unbiased estimator of the target fidelity constructed via random truncation of a telescoping series of the low-fidelity sequence of models. Finally, we discuss and evaluate the proposed multi-fidelity MCMC approach on several applications, including log-Gaussian Cox process modeling, Bayesian ODE system identification, PDE-constrained optimization, and Gaussian process regression parameter inference.

Active multi-fidelity Bayesian online changepoint detection

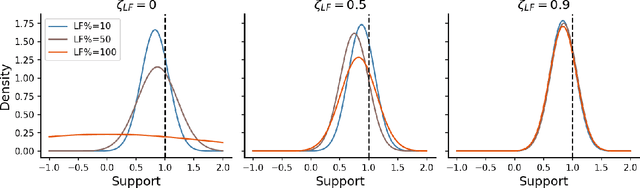
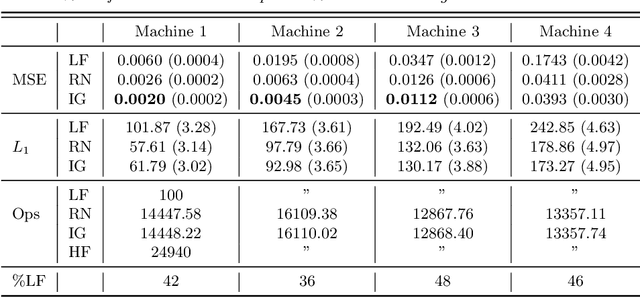
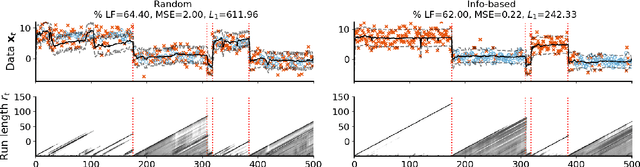
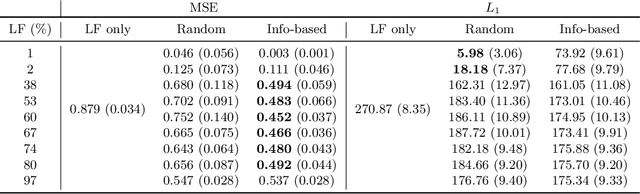
Online algorithms for detecting changepoints, or abrupt shifts in the behavior of a time series, are often deployed with limited resources, e.g., to edge computing settings such as mobile phones or industrial sensors. In these scenarios it may be beneficial to trade the cost of collecting an environmental measurement against the quality or "fidelity" of this measurement and how the measurement affects changepoint estimation. For instance, one might decide between inertial measurements or GPS to determine changepoints for motion. A Bayesian approach to changepoint detection is particularly appealing because we can represent our posterior uncertainty about changepoints and make active, cost-sensitive decisions about data fidelity to reduce this posterior uncertainty. Moreover, the total cost could be dramatically lowered through active fidelity switching, while remaining robust to changes in data distribution. We propose a multi-fidelity approach that makes cost-sensitive decisions about which data fidelity to collect based on maximizing information gain with respect to changepoints. We evaluate this framework on synthetic, video, and audio data and show that this information-based approach results in accurate predictions while reducing total cost.

Finite mixture models are typically inconsistent for the number of components

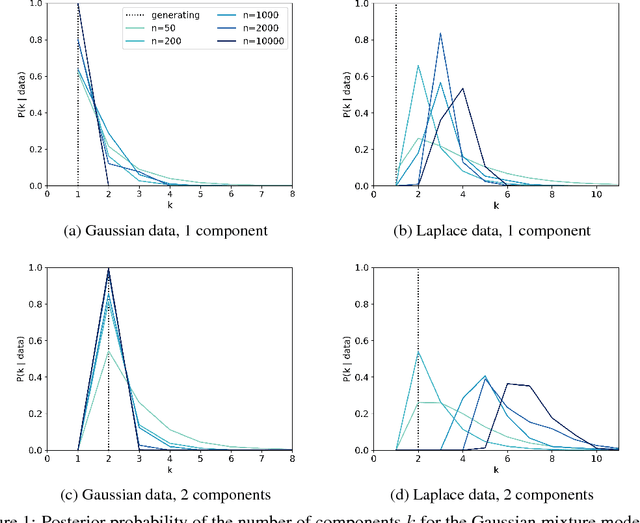
Scientists and engineers are often interested in learning the number of subpopulations (or components) present in a data set. Practitioners commonly use a Dirichlet process mixture model (DPMM) for this purpose; in particular, they count the number of clusters---i.e. components containing at least one data point---in the DPMM posterior. But Miller and Harrison (2013) warn that the DPMM cluster-count posterior is severely inconsistent for the number of latent components when the data are truly generated from a finite mixture; that is, the cluster-count posterior probability on the true generating number of components goes to zero in the limit of infinite data. A potential alternative is to use a finite mixture model (FMM) with a prior on the number of components. Past work has shown the resulting FMM component-count posterior is consistent. But existing results crucially depend on the assumption that the component likelihoods are perfectly specified. In practice, this assumption is unrealistic, and empirical evidence (Miller and Dunson, 2019) suggests that the FMM posterior on the number of components is sensitive to the likelihood choice. In this paper, we add rigor to data-analysis folk wisdom by proving that under even the slightest model misspecification, the FMM posterior on the number of components is ultraseverely inconsistent: for any finite $k \in \mathbb{N}$, the posterior probability that the number of components is $k$ converges to 0 in the limit of infinite data. We illustrate practical consequences of our theory on simulated and real data sets.

Weighted Meta-Learning

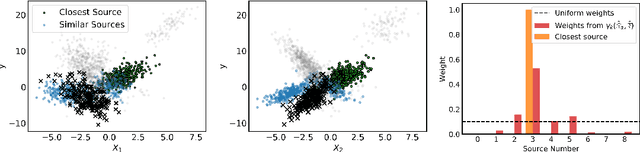
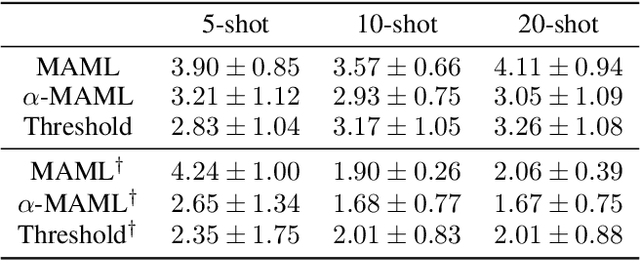
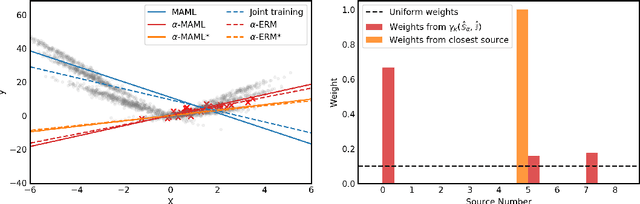
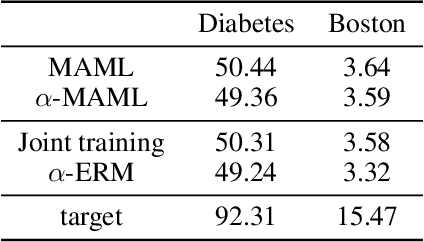
Meta-learning leverages related source tasks to learn an initialization that can be quickly fine-tuned to a target task with limited labeled examples. However, many popular meta-learning algorithms, such as model-agnostic meta-learning (MAML), only assume access to the target samples for fine-tuning. In this work, we provide a general framework for meta-learning based on weighting the loss of different source tasks, where the weights are allowed to depend on the target samples. In this general setting, we provide upper bounds on the distance of the weighted empirical risk of the source tasks and expected target risk in terms of an integral probability metric (IPM) and Rademacher complexity, which apply to a number of meta-learning settings including MAML and a weighted MAML variant. We then develop a learning algorithm based on minimizing the error bound with respect to an empirical IPM, including a weighted MAML algorithm, $\alpha$-MAML. Finally, we demonstrate empirically on several regression problems that our weighted meta-learning algorithm is able to find better initializations than uniformly-weighted meta-learning algorithms, such as MAML.

Edge-exchangeable graphs and sparsity (NIPS 2016)

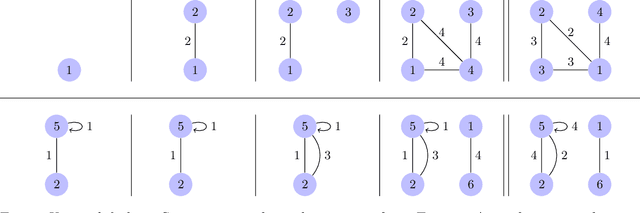
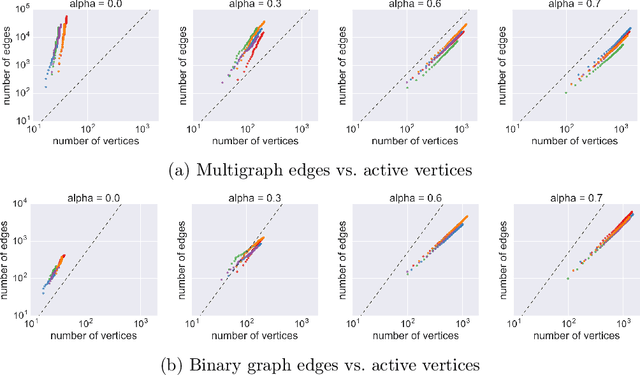
Many popular network models rely on the assumption of (vertex) exchangeability, in which the distribution of the graph is invariant to relabelings of the vertices. However, the Aldous-Hoover theorem guarantees that these graphs are dense or empty with probability one, whereas many real-world graphs are sparse. We present an alternative notion of exchangeability for random graphs, which we call edge exchangeability, in which the distribution of a graph sequence is invariant to the order of the edges. We demonstrate that edge-exchangeable models, unlike models that are traditionally vertex exchangeable, can exhibit sparsity. To do so, we outline a general framework for graph generative models; by contrast to the pioneering work of Caron and Fox (2015), models within our framework are stationary across steps of the graph sequence. In particular, our model grows the graph by instantiating more latent atoms of a single random measure as the dataset size increases, rather than adding new atoms to the measure.

Priors on exchangeable directed graphs

Directed graphs occur throughout statistical modeling of networks, and exchangeability is a natural assumption when the ordering of vertices does not matter. There is a deep structural theory for exchangeable undirected graphs, which extends to the directed case via measurable objects known as digraphons. Using digraphons, we first show how to construct models for exchangeable directed graphs, including special cases such as tournaments, linear orderings, directed acyclic graphs, and partial orderings. We then show how to construct priors on digraphons via the infinite relational digraphon model (di-IRM), a new Bayesian nonparametric block model for exchangeable directed graphs, and demonstrate inference on synthetic data.