No Trick, No Treat: Pursuits and Challenges Towards Simulation-free Training of Neural Samplers

We consider the sampling problem, where the aim is to draw samples from a distribution whose density is known only up to a normalization constant. Recent breakthroughs in generative modeling to approximate a high-dimensional data distribution have sparked significant interest in developing neural network-based methods for this challenging problem. However, neural samplers typically incur heavy computational overhead due to simulating trajectories during training. This motivates the pursuit of simulation-free training procedures of neural samplers. In this work, we propose an elegant modification to previous methods, which allows simulation-free training with the help of a time-dependent normalizing flow. However, it ultimately suffers from severe mode collapse. On closer inspection, we find that nearly all successful neural samplers rely on Langevin preconditioning to avoid mode collapsing. We systematically analyze several popular methods with various objective functions and demonstrate that, in the absence of Langevin preconditioning, most of them fail to adequately cover even a simple target. Finally, we draw attention to a strong baseline by combining the state-of-the-art MCMC method, Parallel Tempering (PT), with an additional generative model to shed light on future explorations of neural samplers.

Position: Multimodal Large Language Models Can Significantly Advance Scientific Reasoning

Scientific reasoning, the process through which humans apply logic, evidence, and critical thinking to explore and interpret scientific phenomena, is essential in advancing knowledge reasoning across diverse fields. However, despite significant progress, current scientific reasoning models still struggle with generalization across domains and often fall short of multimodal perception. Multimodal Large Language Models (MLLMs), which integrate text, images, and other modalities, present an exciting opportunity to overcome these limitations and enhance scientific reasoning. Therefore, this position paper argues that MLLMs can significantly advance scientific reasoning across disciplines such as mathematics, physics, chemistry, and biology. First, we propose a four-stage research roadmap of scientific reasoning capabilities, and highlight the current state of MLLM applications in scientific reasoning, noting their ability to integrate and reason over diverse data types. Second, we summarize the key challenges that remain obstacles to achieving MLLM's full potential. To address these challenges, we propose actionable insights and suggestions for the future. Overall, our work offers a novel perspective on MLLM integration with scientific reasoning, providing the LLM community with a valuable vision for achieving Artificial General Intelligence (AGI).

AiSciVision: A Framework for Specializing Large Multimodal Models in Scientific Image Classification

Trust and interpretability are crucial for the use of Artificial Intelligence (AI) in scientific research, but current models often operate as black boxes offering limited transparency and justifications for their outputs. We introduce AiSciVision, a framework that specializes Large Multimodal Models (LMMs) into interactive research partners and classification models for image classification tasks in niche scientific domains. Our framework uses two key components: (1) Visual Retrieval-Augmented Generation (VisRAG) and (2) domain-specific tools utilized in an agentic workflow. To classify a target image, AiSciVision first retrieves the most similar positive and negative labeled images as context for the LMM. Then the LMM agent actively selects and applies tools to manipulate and inspect the target image over multiple rounds, refining its analysis before making a final prediction. These VisRAG and tooling components are designed to mirror the processes of domain experts, as humans often compare new data to similar examples and use specialized tools to manipulate and inspect images before arriving at a conclusion. Each inference produces both a prediction and a natural language transcript detailing the reasoning and tool usage that led to the prediction. We evaluate AiSciVision on three real-world scientific image classification datasets: detecting the presence of aquaculture ponds, diseased eelgrass, and solar panels. Across these datasets, our method outperforms fully supervised models in low and full-labeled data settings. AiSciVision is actively deployed in real-world use, specifically for aquaculture research, through a dedicated web application that displays and allows the expert users to converse with the transcripts. This work represents a crucial step toward AI systems that are both interpretable and effective, advancing their use in scientific research and scientific discovery.

A new perspective on building efficient and expressive 3D equivariant graph neural networks

Geometric deep learning enables the encoding of physical symmetries in modeling 3D objects. Despite rapid progress in encoding 3D symmetries into Graph Neural Networks (GNNs), a comprehensive evaluation of the expressiveness of these networks through a local-to-global analysis lacks today. In this paper, we propose a local hierarchy of 3D isomorphism to evaluate the expressive power of equivariant GNNs and investigate the process of representing global geometric information from local patches. Our work leads to two crucial modules for designing expressive and efficient geometric GNNs; namely local substructure encoding (LSE) and frame transition encoding (FTE). To demonstrate the applicability of our theory, we propose LEFTNet which effectively implements these modules and achieves state-of-the-art performance on both scalar-valued and vector-valued molecular property prediction tasks. We further point out the design space for future developments of equivariant graph neural networks. Our codes are available at \url{https://github.com/yuanqidu/LeftNet}.

Xtal2DoS: Attention-based Crystal to Sequence Learning for Density of States Prediction

Modern machine learning techniques have been extensively applied to materials science, especially for property prediction tasks. A majority of these methods address scalar property predictions, while more challenging spectral properties remain less emphasized. We formulate a crystal-to-sequence learning task and propose a novel attention-based learning method, Xtal2DoS, which decodes the sequential representation of the material density of states (DoS) properties by incorporating the learned atomic embeddings through attention networks. Experiments show Xtal2DoS is faster than the existing models, and consistently outperforms other state-of-the-art methods on four metrics for two fundamental spectral properties, phonon and electronic DoS.

Structure-based Drug Design with Equivariant Diffusion Models

Structure-based drug design (SBDD) aims to design small-molecule ligands that bind with high affinity and specificity to pre-determined protein targets. Traditional SBDD pipelines start with large-scale docking of compound libraries from public databases, thus limiting the exploration of chemical space to existent previously studied regions. Recent machine learning methods approached this problem using an atom-by-atom generation approach, which is computationally expensive. In this paper, we formulate SBDD as a 3D-conditional generation problem and present DiffSBDD, an E(3)-equivariant 3D-conditional diffusion model that generates novel ligands conditioned on protein pockets. Furthermore, we curate a new dataset of experimentally determined binding complex data from Binding MOAD to provide a realistic binding scenario that complements the synthetic CrossDocked dataset. Comprehensive in silico experiments demonstrate the efficiency of DiffSBDD in generating novel and diverse drug-like ligands that engage protein pockets with high binding energies as predicted by in silico docking.

Left Heavy Tails and the Effectiveness of the Policy and Value Networks in DNN-based best-first search for Sokoban Planning

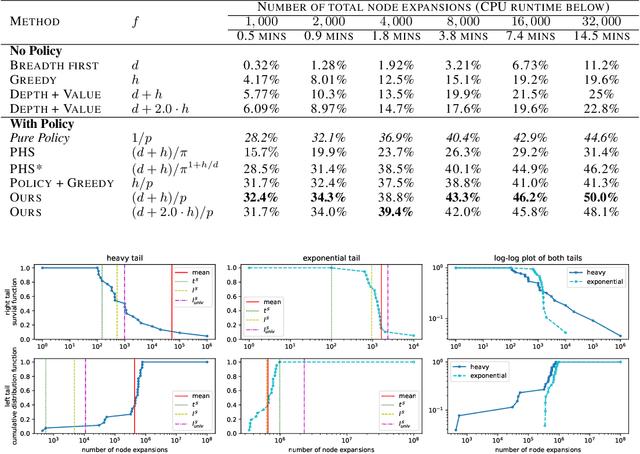
Despite the success of practical solvers in various NP-complete domains such as SAT and CSP as well as using deep reinforcement learning to tackle two-player games such as Go, certain classes of PSPACE-hard planning problems have remained out of reach. Even carefully designed domain-specialized solvers can fail quickly due to the exponential search space on hard instances. Recent works that combine traditional search methods, such as best-first search and Monte Carlo tree search, with Deep Neural Networks' (DNN) heuristics have shown promising progress and can solve a significant number of hard planning instances beyond specialized solvers. To better understand why these approaches work, we studied the interplay of the policy and value networks of DNN-based best-first search on Sokoban and show the surprising effectiveness of the policy network, further enhanced by the value network, as a guiding heuristic for the search. To further understand the phenomena, we studied the cost distribution of the search algorithms and found that Sokoban instances can have heavy-tailed runtime distributions, with tails both on the left and right-hand sides. In particular, for the first time, we show the existence of \textit{left heavy tails} and propose an abstract tree model that can empirically explain the appearance of these tails. The experiments show the critical role of the policy network as a powerful heuristic guiding the search, which can lead to left heavy tails with polynomial scaling by avoiding exploring exponentially sized subtrees. Our results also demonstrate the importance of random restarts, as are widely used in traditional combinatorial solvers, for DNN-based search methods to avoid left and right heavy tails.

Scalable First-Order Bayesian Optimization via Structured Automatic Differentiation

Bayesian Optimization (BO) has shown great promise for the global optimization of functions that are expensive to evaluate, but despite many successes, standard approaches can struggle in high dimensions. To improve the performance of BO, prior work suggested incorporating gradient information into a Gaussian process surrogate of the objective, giving rise to kernel matrices of size $nd \times nd$ for $n$ observations in $d$ dimensions. Na\"ively multiplying with (resp. inverting) these matrices requires $\mathcal{O}(n^2d^2)$ (resp. $\mathcal{O}(n^3d^3$)) operations, which becomes infeasible for moderate dimensions and sample sizes. Here, we observe that a wide range of kernels gives rise to structured matrices, enabling an exact $\mathcal{O}(n^2d)$ matrix-vector multiply for gradient observations and $\mathcal{O}(n^2d^2)$ for Hessian observations. Beyond canonical kernel classes, we derive a programmatic approach to leveraging this type of structure for transformations and combinations of the discussed kernel classes, which constitutes a structure-aware automatic differentiation algorithm. Our methods apply to virtually all canonical kernels and automatically extend to complex kernels, like the neural network, radial basis function network, and spectral mixture kernels without any additional derivations, enabling flexible, problem-dependent modeling while scaling first-order BO to high $d$.

Constrained Machine Learning: The Bagel Framework

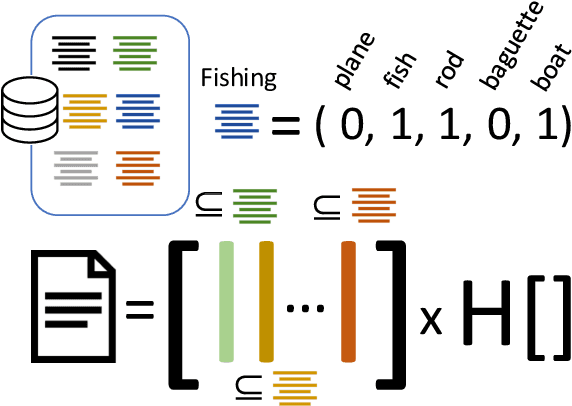
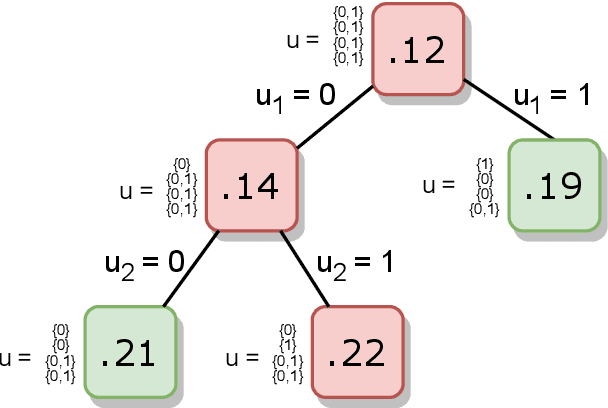
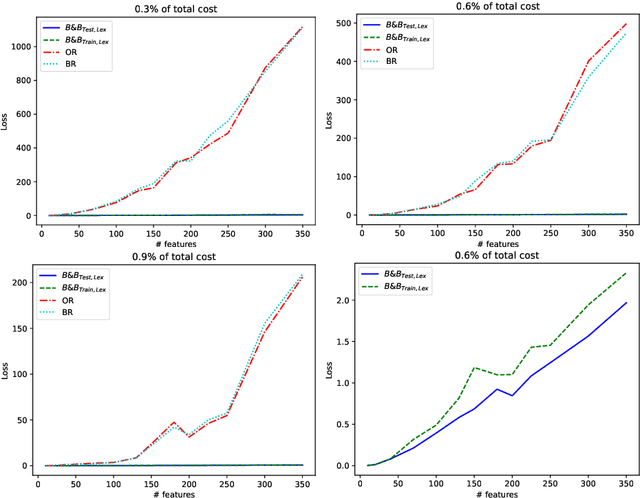
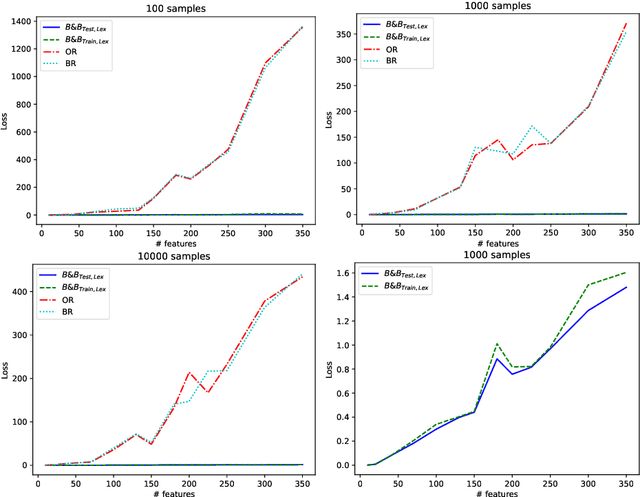
Machine learning models are widely used for real-world applications, such as document analysis and vision. Constrained machine learning problems are problems where learned models have to both be accurate and respect constraints. For continuous convex constraints, many works have been proposed, but learning under combinatorial constraints is still a hard problem. The goal of this paper is to broaden the modeling capacity of constrained machine learning problems by incorporating existing work from combinatorial optimization. We propose first a general framework called BaGeL (Branch, Generate and Learn) which applies Branch and Bound to constrained learning problems where a learning problem is generated and trained at each node until only valid models are obtained. Because machine learning has specific requirements, we also propose an extended table constraint to split the space of hypotheses. We validate the approach on two examples: a linear regression under configuration constraints and a non-negative matrix factorization with prior knowledge for latent semantics analysis.

Contrastively Disentangled Sequential Variational Autoencoder

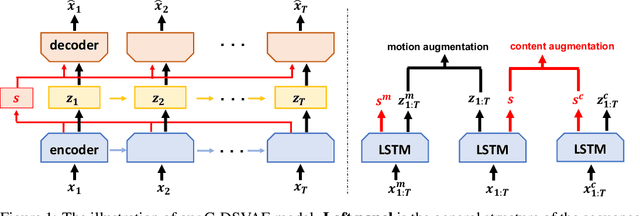
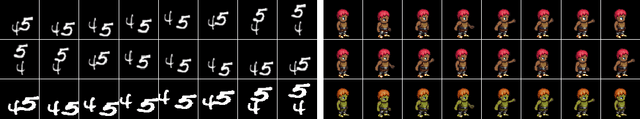
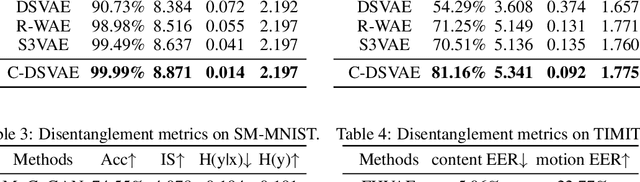
Self-supervised disentangled representation learning is a critical task in sequence modeling. The learnt representations contribute to better model interpretability as well as the data generation, and improve the sample efficiency for downstream tasks. We propose a novel sequence representation learning method, named Contrastively Disentangled Sequential Variational Autoencoder (C-DSVAE), to extract and separate the static (time-invariant) and dynamic (time-variant) factors in the latent space. Different from previous sequential variational autoencoder methods, we use a novel evidence lower bound which maximizes the mutual information between the input and the latent factors, while penalizes the mutual information between the static and dynamic factors. We leverage contrastive estimations of the mutual information terms in training, together with simple yet effective augmentation techniques, to introduce additional inductive biases. Our experiments show that C-DSVAE significantly outperforms the previous state-of-the-art methods on multiple metrics.