Selling Joint Ads: A Regret Minimization Perspective

Motivated by online retail, we consider the problem of selling one item (e.g., an ad slot) to two non-excludable buyers (say, a merchant and a brand). This problem captures, for example, situations where a merchant and a brand cooperatively bid in an auction to advertise a product, and both benefit from the ad being shown. A mechanism collects bids from the two and decides whether to allocate and which payments the two parties should make. This gives rise to intricate incentive compatibility constraints, e.g., on how to split payments between the two parties. We approach the problem of finding a revenue-maximizing incentive-compatible mechanism from an online learning perspective; this poses significant technical challenges. First, the action space (the class of all possible mechanisms) is huge; second, the function that maps mechanisms to revenue is highly irregular, ruling out standard discretization-based approaches. In the stochastic setting, we design an efficient learning algorithm achieving a regret bound of $O(T^{3/4})$. Our approach is based on an adaptive discretization scheme of the space of mechanisms, as any non-adaptive discretization fails to achieve sublinear regret. In the adversarial setting, we exploit the non-Lipschitzness of the problem to prove a strong negative result, namely that no learning algorithm can achieve more than half of the revenue of the best fixed mechanism in hindsight. We then consider the $\sigma$-smooth adversary; we construct an efficient learning algorithm that achieves a regret bound of $O(T^{2/3})$ and builds on a succinct encoding of exponentially many experts. Finally, we prove that no learning algorithm can achieve less than $\Omega(\sqrt T)$ regret in both the stochastic and the smooth setting, thus narrowing the range where the minimax regret rates for these two problems lie.

Learning from Aggregate responses: Instance Level versus Bag Level Loss Functions

Due to the rise of privacy concerns, in many practical applications the training data is aggregated before being shared with the learner, in order to protect privacy of users' sensitive responses. In an aggregate learning framework, the dataset is grouped into bags of samples, where each bag is available only with an aggregate response, providing a summary of individuals' responses in that bag. In this paper, we study two natural loss functions for learning from aggregate responses: bag-level loss and the instance-level loss. In the former, the model is learnt by minimizing a loss between aggregate responses and aggregate model predictions, while in the latter the model aims to fit individual predictions to the aggregate responses. In this work, we show that the instance-level loss can be perceived as a regularized form of the bag-level loss. This observation lets us compare the two approaches with respect to bias and variance of the resulting estimators, and introduce a novel interpolating estimator which combines the two approaches. For linear regression tasks, we provide a precise characterization of the risk of the interpolating estimator in an asymptotic regime where the size of the training set grows in proportion to the features dimension. Our analysis allows us to theoretically understand the effect of different factors, such as bag size on the model prediction risk. In addition, we propose a mechanism for differentially private learning from aggregate responses and derive the optimal bag size in terms of prediction risk-privacy trade-off. We also carry out thorough experiments to corroborate our theory and show the efficacy of the interpolating estimator.

Optimal Unbiased Randomizers for Regression with Label Differential Privacy

We propose a new family of label randomizers for training regression models under the constraint of label differential privacy (DP). In particular, we leverage the trade-offs between bias and variance to construct better label randomizers depending on a privately estimated prior distribution over the labels. We demonstrate that these randomizers achieve state-of-the-art privacy-utility trade-offs on several datasets, highlighting the importance of reducing bias when training neural networks with label DP. We also provide theoretical results shedding light on the structural properties of the optimal unbiased randomizers.

Follow-ups Also Matter: Improving Contextual Bandits via Post-serving Contexts

Standard contextual bandit problem assumes that all the relevant contexts are observed before the algorithm chooses an arm. This modeling paradigm, while useful, often falls short when dealing with problems in which valuable additional context can be observed after arm selection. For example, content recommendation platforms like Youtube, Instagram, Tiktok also observe valuable follow-up information pertinent to the user's reward after recommendation (e.g., how long the user stayed, what is the user's watch speed, etc.). To improve online learning efficiency in these applications, we study a novel contextual bandit problem with post-serving contexts and design a new algorithm, poLinUCB, that achieves tight regret under standard assumptions. Core to our technical proof is a robustified and generalized version of the well-known Elliptical Potential Lemma (EPL), which can accommodate noise in data. Such robustification is necessary for tackling our problem, and we believe it could also be of general interest. Extensive empirical tests on both synthetic and real-world datasets demonstrate the significant benefit of utilizing post-serving contexts as well as the superior performance of our algorithm over the state-of-the-art approaches.

Incrementality Bidding via Reinforcement Learning under Mixed and Delayed Rewards

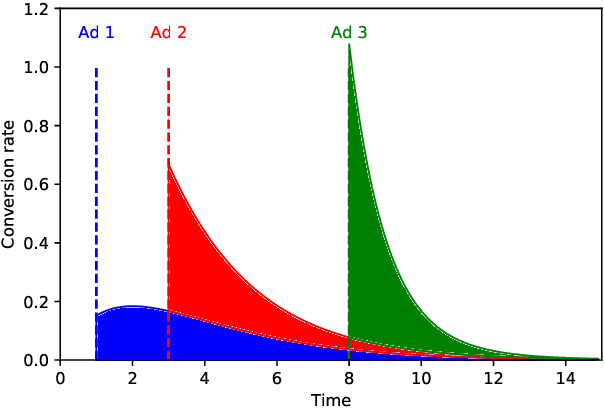
Incrementality, which is used to measure the causal effect of showing an ad to a potential customer (e.g. a user in an internet platform) versus not, is a central object for advertisers in online advertising platforms. This paper investigates the problem of how an advertiser can learn to optimize the bidding sequence in an online manner \emph{without} knowing the incrementality parameters in advance. We formulate the offline version of this problem as a specially structured episodic Markov Decision Process (MDP) and then, for its online learning counterpart, propose a novel reinforcement learning (RL) algorithm with regret at most $\widetilde{O}(H^2\sqrt{T})$, which depends on the number of rounds $H$ and number of episodes $T$, but does not depend on the number of actions (i.e., possible bids). A fundamental difference between our learning problem from standard RL problems is that the realized reward feedback from conversion incrementality is \emph{mixed} and \emph{delayed}. To handle this difficulty we propose and analyze a novel pairwise moment-matching algorithm to learn the conversion incrementality, which we believe is of independent of interest.

Learning to Bid in Contextual First Price Auctions

In this paper, we investigate the problem about how to bid in repeated contextual first price auctions. We consider a single bidder (learner) who repeatedly bids in the first price auctions: at each time $t$, the learner observes a context $x_t\in \mathbb{R}^d$ and decides the bid based on historical information and $x_t$. We assume a structured linear model of the maximum bid of all the others $m_t = \alpha_0\cdot x_t + z_t$, where $\alpha_0\in \mathbb{R}^d$ is unknown to the learner and $z_t$ is randomly sampled from a noise distribution $\mathcal{F}$ with log-concave density function $f$. We consider both \emph{binary feedback} (the learner can only observe whether she wins or not) and \emph{full information feedback} (the learner can observe $m_t$) at the end of each time $t$. For binary feedback, when the noise distribution $\mathcal{F}$ is known, we propose a bidding algorithm, by using maximum likelihood estimation (MLE) method to achieve at most $\widetilde{O}(\sqrt{\log(d) T})$ regret. Moreover, we generalize this algorithm to the setting with binary feedback and the noise distribution is unknown but belongs to a parametrized family of distributions. For the full information feedback with \emph{unknown} noise distribution, we provide an algorithm that achieves regret at most $\widetilde{O}(\sqrt{dT})$. Our approach combines an estimator for log-concave density functions and then MLE method to learn the noise distribution $\mathcal{F}$ and linear weight $\alpha_0$ simultaneously. We also provide a lower bound result such that any bidding policy in a broad class must achieve regret at least $\Omega(\sqrt{T})$, even when the learner receives the full information feedback and $\mathcal{F}$ is known.

Online Learning via Offline Greedy Algorithms: Applications in Market Design and Optimization

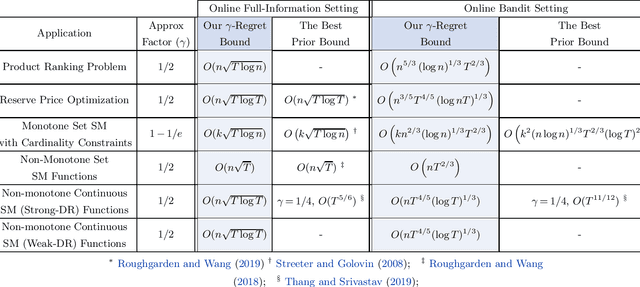
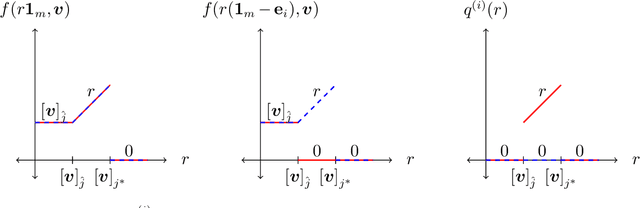
Motivated by online decision-making in time-varying combinatorial environments, we study the problem of transforming offline algorithms to their online counterparts. We focus on offline combinatorial problems that are amenable to a constant factor approximation using a greedy algorithm that is robust to local errors. For such problems, we provide a general framework that efficiently transforms offline robust greedy algorithms to online ones using Blackwell approachability. We show that the resulting online algorithms have $O(\sqrt{T})$ (approximate) regret under the full information setting. We further introduce a bandit extension of Blackwell approachability that we call Bandit Blackwell approachability. We leverage this notion to transform greedy robust offline algorithms into a $O(T^{2/3})$ (approximate) regret in the bandit setting. Demonstrating the flexibility of our framework, we apply our offline-to-online transformation to several problems at the intersection of revenue management, market design, and online optimization, including product ranking optimization in online platforms, reserve price optimization in auctions, and submodular maximization. We show that our transformation, when applied to these applications, leads to new regret bounds or improves the current known bounds.

Handling many conversions per click in modeling delayed feedback

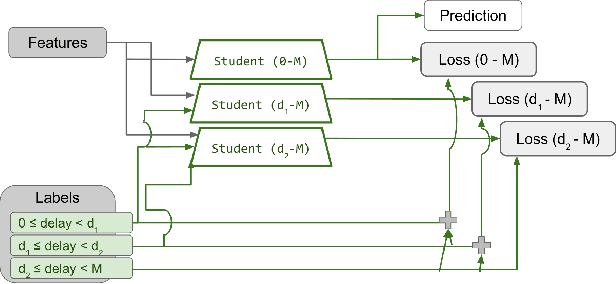
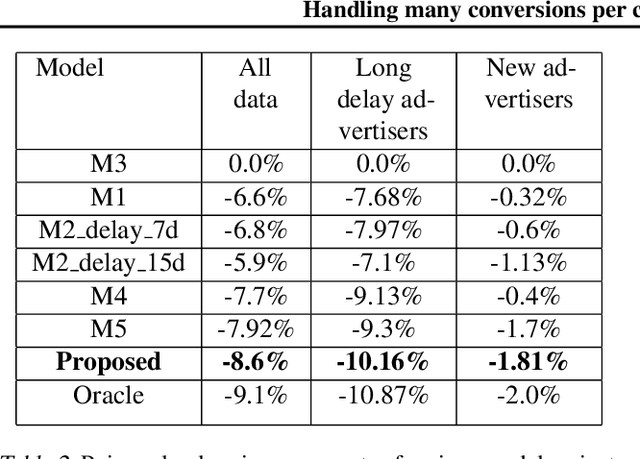
Predicting the expected value or number of post-click conversions (purchases or other events) is a key task in performance-based digital advertising. In training a conversion optimizer model, one of the most crucial aspects is handling delayed feedback with respect to conversions, which can happen multiple times with varying delay. This task is difficult, as the delay distribution is different for each advertiser, is long-tailed, often does not follow any particular class of parametric distributions, and can change over time. We tackle these challenges using an unbiased estimation model based on three core ideas. The first idea is to split the label as a sum of labels with different delay buckets, each of which trains only on mature label, the second is to use thermometer encoding to increase accuracy and reduce inference cost, and the third is to use auxiliary information to increase the stability of the model and to handle drift in the distribution.

Submodular Maximization Through Barrier Functions

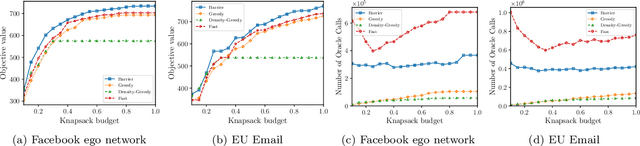
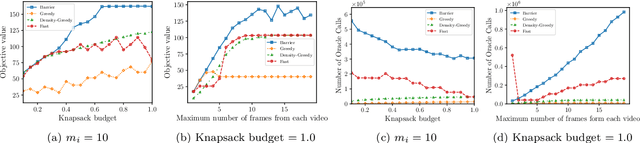
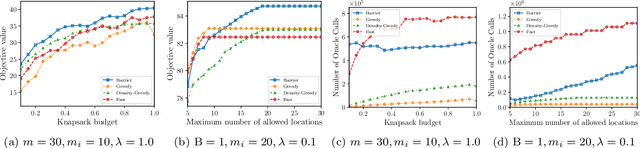
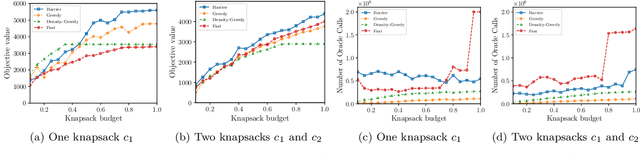
In this paper, we introduce a novel technique for constrained submodular maximization, inspired by barrier functions in continuous optimization. This connection not only improves the running time for constrained submodular maximization but also provides the state of the art guarantee. More precisely, for maximizing a monotone submodular function subject to the combination of a $k$-matchoid and $\ell$-knapsack constraint (for $\ell\leq k$), we propose a potential function that can be approximately minimized. Once we minimize the potential function up to an $\epsilon$ error it is guaranteed that we have found a feasible set with a $2(k+1+\epsilon)$-approximation factor which can indeed be further improved to $(k+1+\epsilon)$ by an enumeration technique. We extensively evaluate the performance of our proposed algorithm over several real-world applications, including a movie recommendation system, summarization tasks for YouTube videos, Twitter feeds and Yelp business locations, and a set cover problem.

Bandits with Knapsacks

Multi-armed bandit problems are the predominant theoretical model of exploration-exploitation tradeoffs in learning, and they have countless applications ranging from medical trials, to communication networks, to Web search and advertising. In many of these application domains the learner may be constrained by one or more supply (or budget) limits, in addition to the customary limitation on the time horizon. The literature lacks a general model encompassing these sorts of problems. We introduce such a model, called "bandits with knapsacks", that combines aspects of stochastic integer programming with online learning. A distinctive feature of our problem, in comparison to the existing regret-minimization literature, is that the optimal policy for a given latent distribution may significantly outperform the policy that plays the optimal fixed arm. Consequently, achieving sublinear regret in the bandits-with-knapsacks problem is significantly more challenging than in conventional bandit problems. We present two algorithms whose reward is close to the information-theoretic optimum: one is based on a novel "balanced exploration" paradigm, while the other is a primal-dual algorithm that uses multiplicative updates. Further, we prove that the regret achieved by both algorithms is optimal up to polylogarithmic factors. We illustrate the generality of the problem by presenting applications in a number of different domains including electronic commerce, routing, and scheduling. As one example of a concrete application, we consider the problem of dynamic posted pricing with limited supply and obtain the first algorithm whose regret, with respect to the optimal dynamic policy, is sublinear in the supply.