Full Swap Regret and Discretized Calibration

We study the problem of minimizing swap regret in structured normal-form games. Players have a very large (potentially infinite) number of pure actions, but each action has an embedding into $d$-dimensional space and payoffs are given by bilinear functions of these embeddings. We provide an efficient learning algorithm for this setting that incurs at most $\tilde{O}(T^{(d+1)/(d+3)})$ swap regret after $T$ rounds. To achieve this, we introduce a new online learning problem we call \emph{full swap regret minimization}. In this problem, a learner repeatedly takes a (randomized) action in a bounded convex $d$-dimensional action set $\mathcal{K}$ and then receives a loss from the adversary, with the goal of minimizing their regret with respect to the \emph{worst-case} swap function mapping $\mathcal{K}$ to $\mathcal{K}$. For varied assumptions about the convexity and smoothness of the loss functions, we design algorithms with full swap regret bounds ranging from $O(T^{d/(d+2)})$ to $O(T^{(d+1)/(d+2)})$. Finally, we apply these tools to the problem of online forecasting to minimize calibration error, showing that several notions of calibration can be viewed as specific instances of full swap regret. In particular, we design efficient algorithms for online forecasting that guarantee at most $O(T^{1/3})$ $\ell_2$-calibration error and $O(\max(\sqrt{\epsilon T}, T^{1/3}))$ \emph{discretized-calibration} error (when the forecaster is restricted to predicting multiples of $\epsilon$).

Near-Optimal Algorithms for Omniprediction

Omnipredictors are simple prediction functions that encode loss-minimizing predictions with respect to a hypothesis class $\mathcal{H}$, simultaneously for every loss function within a class of losses $\mathcal{L}$. In this work, we give near-optimal learning algorithms for omniprediction, in both the online and offline settings. To begin, we give an oracle-efficient online learning algorithm that acheives $(\mathcal{L},\mathcal{H})$-omniprediction with $\tilde{O}(\sqrt{T \log |\mathcal{H}|})$ regret for any class of Lipschitz loss functions $\mathcal{L} \subseteq \mathcal{L}_\mathrm{Lip}$. Quite surprisingly, this regret bound matches the optimal regret for \emph{minimization of a single loss function} (up to a $\sqrt{\log(T)}$ factor). Given this online algorithm, we develop an online-to-offline conversion that achieves near-optimal complexity across a number of measures. In particular, for all bounded loss functions within the class of Bounded Variation losses $\mathcal{L}_\mathrm{BV}$ (which include all convex, all Lipschitz, and all proper losses) and any (possibly-infinite) $\mathcal{H}$, we obtain an offline learning algorithm that, leveraging an (offline) ERM oracle and $m$ samples from $\mathcal{D}$, returns an efficient $(\mathcal{L}_{\mathrm{BV}},\mathcal{H},\varepsilon(m))$-omnipredictor for $\varepsilon(m)$ scaling near-linearly in the Rademacher complexity of $\mathrm{Th} \circ \mathcal{H}$.

Learning in Budgeted Auctions with Spacing Objectives

In many repeated auction settings, participants care not only about how frequently they win but also how their winnings are distributed over time. This problem arises in various practical domains where avoiding congested demand is crucial, such as online retail sales and compute services, as well as in advertising campaigns that require sustained visibility over time. We introduce a simple model of this phenomenon, modeling it as a budgeted auction where the value of a win is a concave function of the time since the last win. This implies that for a given number of wins, even spacing over time is optimal. We also extend our model and results to the case when not all wins result in "conversions" (realization of actual gains), and the probability of conversion depends on a context. The goal is to maximize and evenly space conversions rather than just wins. We study the optimal policies for this setting in second-price auctions and offer learning algorithms for the bidders that achieve low regret against the optimal bidding policy in a Bayesian online setting. Our main result is a computationally efficient online learning algorithm that achieves $\tilde O(\sqrt T)$ regret. We achieve this by showing that an infinite-horizon Markov decision process (MDP) with the budget constraint in expectation is essentially equivalent to our problem, even when limiting that MDP to a very small number of states. The algorithm achieves low regret by learning a bidding policy that chooses bids as a function of the context and the system's state, which will be the time elapsed since the last win (or conversion). We show that state-independent strategies incur linear regret even without uncertainty of conversions. We complement this by showing that there are state-independent strategies that, while still having linear regret, achieve a $(1-\frac 1 e)$ approximation to the optimal reward.

Improved bounds for calibration via stronger sign preservation games

A set of probabilistic forecasts is calibrated if each prediction of the forecaster closely approximates the empirical distribution of outcomes on the subset of timesteps where that prediction was made. We study the fundamental problem of online calibrated forecasting of binary sequences, which was initially studied by Foster & Vohra (1998). They derived an algorithm with $O(T^{2/3})$ calibration error after $T$ time steps, and showed a lower bound of $\Omega(T^{1/2})$. These bounds remained stagnant for two decades, until Qiao & Valiant (2021) improved the lower bound to $\Omega(T^{0.528})$ by introducing a combinatorial game called sign preservation and showing that lower bounds for this game imply lower bounds for calibration. We introduce a strengthening of Qiao & Valiant's game that we call sign preservation with reuse (SPR). We prove that the relationship between SPR and calibrated forecasting is bidirectional: not only do lower bounds for SPR translate into lower bounds for calibration, but algorithms for SPR also translate into new algorithms for calibrated forecasting. In particular, any strategy that improves the trivial upper bound for the value of the SPR game would imply a forecasting algorithm with calibration error exponent less than 2/3, improving Foster & Vohra's upper bound for the first time. Using similar ideas, we then prove a slightly stronger lower bound than that of Qiao & Valiant, namely $\Omega(T^{0.54389})$. Our lower bound is obtained by an oblivious adversary, marking the first $\omega(T^{1/2})$ calibration lower bound for oblivious adversaries.

Faster Recalibration of an Online Predictor via Approachability

Predictive models in ML need to be trustworthy and reliable, which often at the very least means outputting calibrated probabilities. This can be particularly difficult to guarantee in the online prediction setting when the outcome sequence can be generated adversarially. In this paper we introduce a technique using Blackwell's approachability theorem for taking an online predictive model which might not be calibrated and transforming its predictions to calibrated predictions without much increase to the loss of the original model. Our proposed algorithm achieves calibration and accuracy at a faster rate than existing techniques arXiv:1607.03594 and is the first algorithm to offer a flexible tradeoff between calibration error and accuracy in the online setting. We demonstrate this by characterizing the space of jointly achievable calibration and regret using our technique.

U-Calibration: Forecasting for an Unknown Agent

We consider the problem of evaluating forecasts of binary events whose predictions are consumed by rational agents who take an action in response to a prediction, but whose utility is unknown to the forecaster. We show that optimizing forecasts for a single scoring rule (e.g., the Brier score) cannot guarantee low regret for all possible agents. In contrast, forecasts that are well-calibrated guarantee that all agents incur sublinear regret. However, calibration is not a necessary criterion here (it is possible for miscalibrated forecasts to provide good regret guarantees for all possible agents), and calibrated forecasting procedures have provably worse convergence rates than forecasting procedures targeting a single scoring rule. Motivated by this, we present a new metric for evaluating forecasts that we call U-calibration, equal to the maximal regret of the sequence of forecasts when evaluated under any bounded scoring rule. We show that sublinear U-calibration error is a necessary and sufficient condition for all agents to achieve sublinear regret guarantees. We additionally demonstrate how to compute the U-calibration error efficiently and provide an online algorithm that achieves $O(\sqrt{T})$ U-calibration error (on par with optimal rates for optimizing for a single scoring rule, and bypassing lower bounds for the traditionally calibrated learning procedures). Finally, we discuss generalizations to the multiclass prediction setting.

Non-Stochastic CDF Estimation Using Threshold Queries

Estimating the empirical distribution of a scalar-valued data set is a basic and fundamental task. In this paper, we tackle the problem of estimating an empirical distribution in a setting with two challenging features. First, the algorithm does not directly observe the data; instead, it only asks a limited number of threshold queries about each sample. Second, the data are not assumed to be independent and identically distributed; instead, we allow for an arbitrary process generating the samples, including an adaptive adversary. These considerations are relevant, for example, when modeling a seller experimenting with posted prices to estimate the distribution of consumers' willingness to pay for a product: offering a price and observing a consumer's purchase decision is equivalent to asking a single threshold query about their value, and the distribution of consumers' values may be non-stationary over time, as early adopters may differ markedly from late adopters. Our main result quantifies, to within a constant factor, the sample complexity of estimating the empirical CDF of a sequence of elements of $[n]$, up to $\varepsilon$ additive error, using one threshold query per sample. The complexity depends only logarithmically on $n$, and our result can be interpreted as extending the existing logarithmic-complexity results for noisy binary search to the more challenging setting where noise is non-stochastic. Along the way to designing our algorithm, we consider a more general model in which the algorithm is allowed to make a limited number of simultaneous threshold queries on each sample. We solve this problem using Blackwell's Approachability Theorem and the exponential weights method. As a side result of independent interest, we characterize the minimum number of simultaneous threshold queries required by deterministic CDF estimation algorithms.

Non-monotonic Resource Utilization in the Bandits with Knapsacks Problem

Bandits with knapsacks (BwK) is an influential model of sequential decision-making under uncertainty that incorporates resource consumption constraints. In each round, the decision-maker observes an outcome consisting of a reward and a vector of nonnegative resource consumptions, and the budget of each resource is decremented by its consumption. In this paper we introduce a natural generalization of the stochastic BwK problem that allows non-monotonic resource utilization. In each round, the decision-maker observes an outcome consisting of a reward and a vector of resource drifts that can be positive, negative or zero, and the budget of each resource is incremented by its drift. Our main result is a Markov decision process (MDP) policy that has constant regret against a linear programming (LP) relaxation when the decision-maker knows the true outcome distributions. We build upon this to develop a learning algorithm that has logarithmic regret against the same LP relaxation when the decision-maker does not know the true outcome distributions. We also present a reduction from BwK to our model that shows our regret bound matches existing results.

Procrastinating with Confidence: Near-Optimal, Anytime, Adaptive Algorithm Configuration

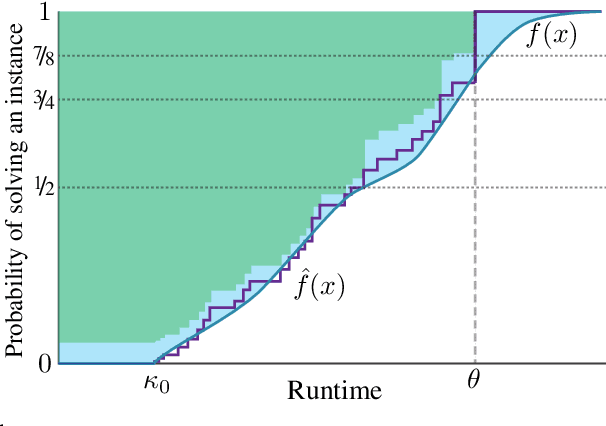
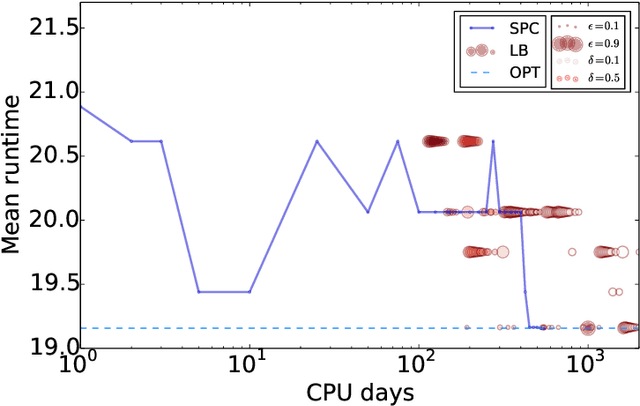
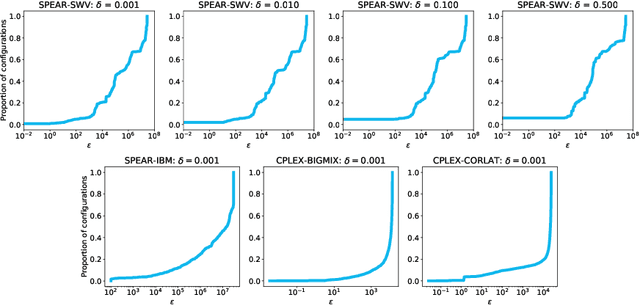
Algorithm configuration methods optimize the performance of a parameterized heuristic algorithm on a given distribution of problem instances. Recent work introduced an algorithm configuration procedure ('Structured Procrastination') that provably achieves near optimal performance with high probability and with nearly minimal runtime in the worst case. It also offers an $\textit{anytime}$ property: it keeps tightening its optimality guarantees the longer it is run. Unfortunately, Structured Procrastination is not $\textit{adaptive}$ to characteristics of the parameterized algorithm: it treats every input like the worst case. Follow-up work ('Leaps and Bounds') achieves adaptivity but trades away the anytime property. This paper introduces a new algorithm configuration method, 'Structured Procrastination with Confidence', that preserves the near-optimality and anytime properties of Structured Procrastination while adding adaptivity. In particular, the new algorithm will perform dramatically faster in settings where many algorithm configurations perform poorly; we show empirically that such settings arise frequently in practice.

An Alternative View: When Does SGD Escape Local Minima?

Stochastic gradient descent (SGD) is widely used in machine learning. Although being commonly viewed as a fast but not accurate version of gradient descent (GD), it always finds better solutions than GD for modern neural networks. In order to understand this phenomenon, we take an alternative view that SGD is working on the convolved (thus smoothed) version of the loss function. We show that, even if the function $f$ has many bad local minima or saddle points, as long as for every point $x$, the weighted average of the gradients of its neighborhoods is one point convex with respect to the desired solution $x^*$, SGD will get close to, and then stay around $x^*$ with constant probability. More specifically, SGD will not get stuck at "sharp" local minima with small diameters, as long as the neighborhoods of these regions contain enough gradient information. The neighborhood size is controlled by step size and gradient noise. Our result identifies a set of functions that SGD provably works, which is much larger than the set of convex functions. Empirically, we observe that the loss surface of neural networks enjoys nice one point convexity properties locally, therefore our theorem helps explain why SGD works so well for neural networks.