Dynamic Matching with Post-allocation Service and its Application to Refugee Resettlement

Motivated by our collaboration with a major refugee resettlement agency in the U.S., we study a dynamic matching problem where each new arrival (a refugee case) must be matched immediately and irrevocably to one of the static resources (a location with a fixed annual quota). In addition to consuming the static resource, each case requires post-allocation service from a server, such as a translator. Given the time-consuming nature of service, a server may not be available at a given time, thus we refer to it as a dynamic resource. Upon matching, the case will wait to avail service in a first-come-first-serve manner. Bursty matching to a location may result in undesirable congestion at its corresponding server. Consequently, the central planner (the agency) faces a dynamic matching problem with an objective that combines the matching reward (captured by pair-specific employment outcomes) with the cost for congestion for dynamic resources and over-allocation for the static ones. Motivated by the observed fluctuations in the composition of refugee pools across the years, we design algorithms that do not rely on distributional knowledge constructed based on past years' data. To that end, we develop learning-based algorithms that are asymptotically optimal in certain regimes, easy to interpret, and computationally fast. Our design is based on learning the dual variables of the underlying optimization problem; however, the main challenge lies in the time-varying nature of the dual variables associated with dynamic resources. To overcome this challenge, our theoretical development brings together techniques from Lyapunov analysis, adversarial online learning, and stochastic optimization. On the application side, when tested on real data from our partner agency, our method outperforms existing ones making it a viable candidate for replacing the current practice upon experimentation.

Misalignment, Learning, and Ranking: Harnessing Users Limited Attention

In digital health and EdTech, recommendation systems face a significant challenge: users often choose impulsively, in ways that conflict with the platform's long-term payoffs. This misalignment makes it difficult to effectively learn to rank items, as it may hinder exploration of items with greater long-term payoffs. Our paper tackles this issue by utilizing users' limited attention spans. We propose a model where a platform presents items with unknown payoffs to the platform in a ranked list to $T$ users over time. Each user selects an item by first considering a prefix window of these ranked items and then picking the highest preferred item in that window (and the platform observes its payoff for this item). We study the design of online bandit algorithms that obtain vanishing regret against hindsight optimal benchmarks. We first consider adversarial window sizes and stochastic iid payoffs. We design an active-elimination-based algorithm that achieves an optimal instance-dependent regret bound of $O(\log(T))$, by showing matching regret upper and lower bounds. The key idea is using the combinatorial structure of the problem to either obtain a large payoff from each item or to explore by getting a sample from that item. This method systematically narrows down the item choices to enhance learning efficiency and payoff. Second, we consider adversarial payoffs and stochastic iid window sizes. We start from the full-information problem of finding the permutation that maximizes the expected payoff. By a novel combinatorial argument, we characterize the polytope of admissible item selection probabilities by a permutation and show it has a polynomial-size representation. Using this representation, we show how standard algorithms for adversarial online linear optimization in the space of admissible probabilities can be used to obtain a polynomial-time algorithm with $O(\sqrt{T})$ regret.

Online Learning via Offline Greedy Algorithms: Applications in Market Design and Optimization

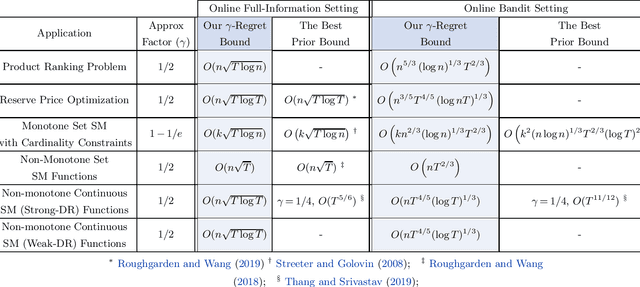
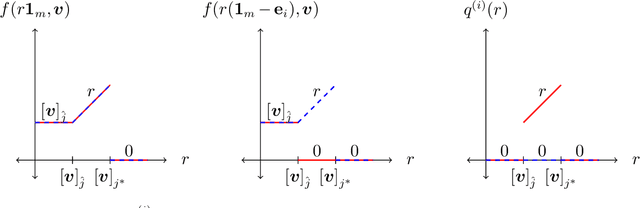
Motivated by online decision-making in time-varying combinatorial environments, we study the problem of transforming offline algorithms to their online counterparts. We focus on offline combinatorial problems that are amenable to a constant factor approximation using a greedy algorithm that is robust to local errors. For such problems, we provide a general framework that efficiently transforms offline robust greedy algorithms to online ones using Blackwell approachability. We show that the resulting online algorithms have $O(\sqrt{T})$ (approximate) regret under the full information setting. We further introduce a bandit extension of Blackwell approachability that we call Bandit Blackwell approachability. We leverage this notion to transform greedy robust offline algorithms into a $O(T^{2/3})$ (approximate) regret in the bandit setting. Demonstrating the flexibility of our framework, we apply our offline-to-online transformation to several problems at the intersection of revenue management, market design, and online optimization, including product ranking optimization in online platforms, reserve price optimization in auctions, and submodular maximization. We show that our transformation, when applied to these applications, leads to new regret bounds or improves the current known bounds.

Multi-scale Online Learning and its Applications to Online Auctions

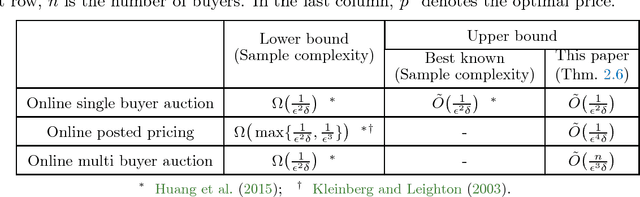
We consider revenue maximization in online auction/pricing problems. A seller sells an identical item in each period to a new buyer, or a new set of buyers. For the online posted pricing problem, we show regret bounds that scale with the best fixed price, rather than the range of the values. We also show regret bounds that are almost scale free, and match the offline sample complexity, when comparing to a benchmark that requires a lower bound on the market share. These results are obtained by generalizing the classical learning from experts and multi-armed bandit problems to their multi-scale versions. In this version, the reward of each action is in a different range, and the regret w.r.t. a given action scales with its own range, rather than the maximum range.

Hierarchical Clustering better than Average-Linkage

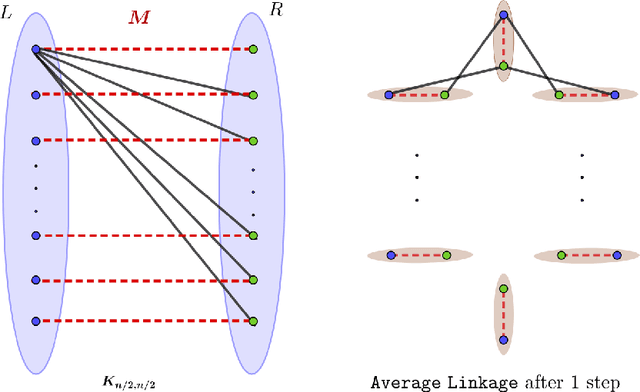
Hierarchical Clustering (HC) is a widely studied problem in exploratory data analysis, usually tackled by simple agglomerative procedures like average-linkage, single-linkage or complete-linkage. In this paper we focus on two objectives, introduced recently to give insight into the performance of average-linkage clustering: a similarity based HC objective proposed by [Moseley and Wang, 2017] and a dissimilarity based HC objective proposed by [Cohen-Addad et al., 2018]. In both cases, we present tight counterexamples showing that average-linkage cannot obtain better than 1/3 and 2/3 approximations respectively (in the worst-case), settling an open question raised in [Moseley and Wang, 2017]. This matches the approximation ratio of a random solution, raising a natural question: can we beat average-linkage for these objectives? We answer this in the affirmative, giving two new algorithms based on semidefinite programming with provably better guarantees.

Hierarchical Clustering with Structural Constraints

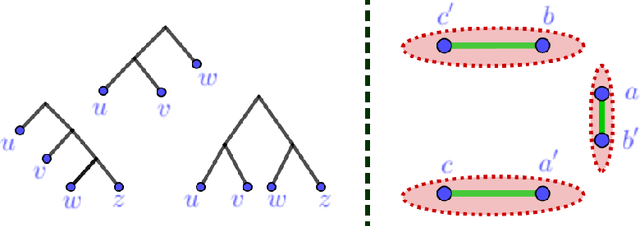
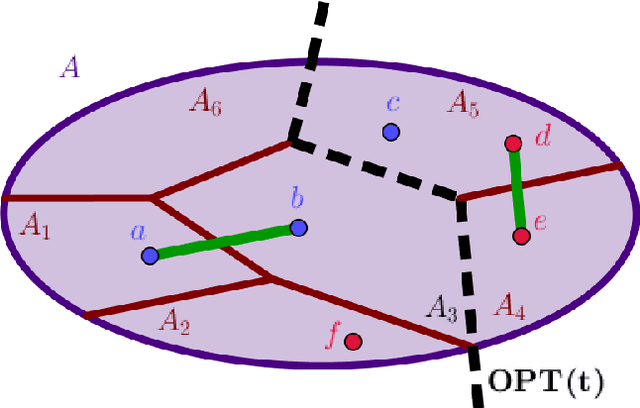
Hierarchical clustering is a popular unsupervised data analysis method. For many real-world applications, we would like to exploit prior information about the data that imposes constraints on the clustering hierarchy, and is not captured by the set of features available to the algorithm. This gives rise to the problem of "hierarchical clustering with structural constraints". Structural constraints pose major challenges for bottom-up approaches like average/single linkage and even though they can be naturally incorporated into top-down divisive algorithms, no formal guarantees exist on the quality of their output. In this paper, we provide provable approximation guarantees for two simple top-down algorithms, using a recently introduced optimization viewpoint of hierarchical clustering with pairwise similarity information [Dasgupta, 2016]. We show how to find good solutions even in the presence of conflicting prior information, by formulating a constraint-based regularization of the objective. We further explore a variation of this objective for dissimilarity information [Cohen-Addad et al., 2018] and improve upon current techniques. Finally, we demonstrate our approach on a real dataset for the taxonomy application.

Optimal Algorithms for Continuous Non-monotone Submodular and DR-Submodular Maximization

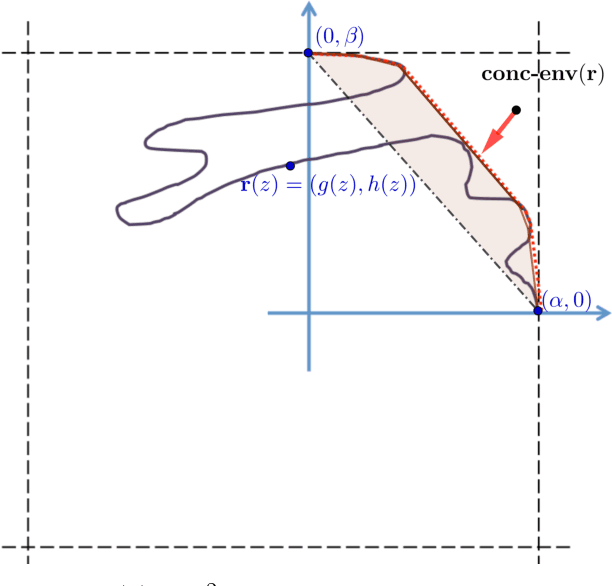
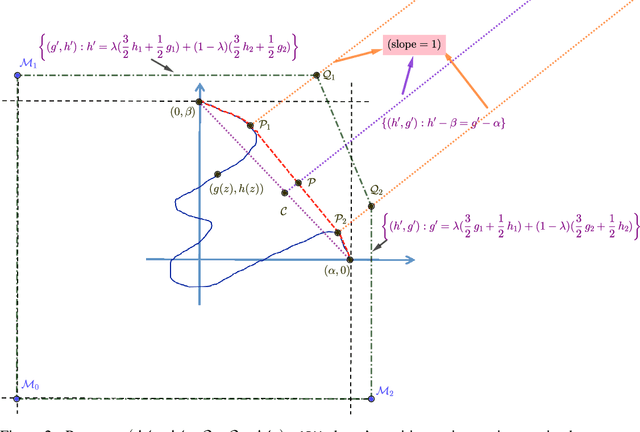
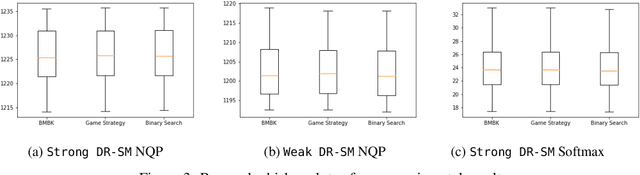
In this paper we study the fundamental problems of maximizing a continuous non-monotone submodular function over the hypercube, both with and without coordinate-wise concavity. This family of optimization problems has several applications in machine learning, economics, and communication systems. Our main result is the first $\frac{1}{2}$-approximation algorithm for continuous submodular function maximization; this approximation factor of $\frac{1}{2}$ is the best possible for algorithms that only query the objective function at polynomially many points. For the special case of DR-submodular maximization, i.e. when the submodular functions is also coordinate wise concave along all coordinates, we provide a different $\frac{1}{2}$-approximation algorithm that runs in quasilinear time. Both of these results improve upon prior work [Bian et al, 2017, Soma and Yoshida, 2017]. Our first algorithm uses novel ideas such as reducing the guaranteed approximation problem to analyzing a zero-sum game for each coordinate, and incorporates the geometry of this zero-sum game to fix the value at this coordinate. Our second algorithm exploits coordinate-wise concavity to identify a monotone equilibrium condition sufficient for getting the required approximation guarantee, and hunts for the equilibrium point using binary search. We further run experiments to verify the performance of our proposed algorithms in related machine learning applications.

Truth and Regret in Online Scheduling

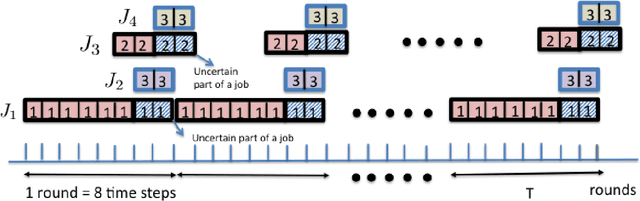
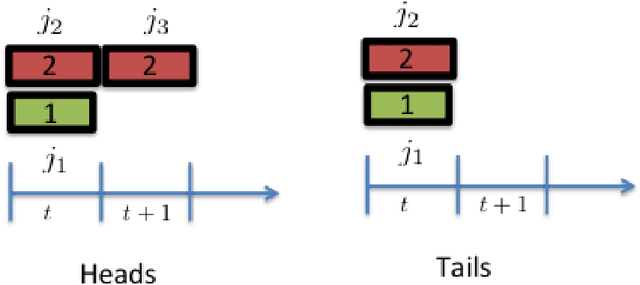
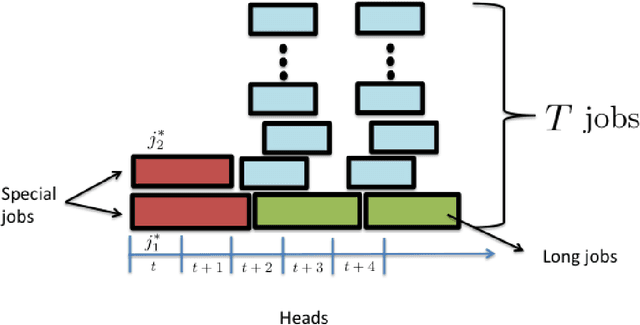
We consider a scheduling problem where a cloud service provider has multiple units of a resource available over time. Selfish clients submit jobs, each with an arrival time, deadline, length, and value. The service provider's goal is to implement a truthful online mechanism for scheduling jobs so as to maximize the social welfare of the schedule. Recent work shows that under a stochastic assumption on job arrivals, there is a single-parameter family of mechanisms that achieves near-optimal social welfare. We show that given any such family of near-optimal online mechanisms, there exists an online mechanism that in the worst case performs nearly as well as the best of the given mechanisms. Our mechanism is truthful whenever the mechanisms in the given family are truthful and prompt, and achieves optimal (within constant factors) regret. We model the problem of competing against a family of online scheduling mechanisms as one of learning from expert advice. A primary challenge is that any scheduling decisions we make affect not only the payoff at the current step, but also the resource availability and payoffs in future steps. Furthermore, switching from one algorithm (a.k.a. expert) to another in an online fashion is challenging both because it requires synchronization with the state of the latter algorithm as well as because it affects the incentive structure of the algorithms. We further show how to adapt our algorithm to a non-clairvoyant setting where job lengths are unknown until jobs are run to completion. Once again, in this setting, we obtain truthfulness along with asymptotically optimal regret (within poly-logarithmic factors).

On the Achievability of Cramér-Rao Bound In Noisy Compressed Sensing

Recently, it has been proved in Babadi et al. that in noisy compressed sensing, a joint typical estimator can asymptotically achieve the Cramer-Rao lower bound of the problem.To prove this result, this paper used a lemma,which is provided in Akcakaya et al,that comprises the main building block of the proof. This lemma is based on the assumption of Gaussianity of the measurement matrix and its randomness in the domain of noise. In this correspondence, we generalize the results obtained in Babadi et al by dropping the Gaussianity assumption on the measurement matrix. In fact, by considering the measurement matrix as a deterministic matrix in our analysis, we find a theorem similar to the main theorem of Babadi et al for a family of randomly generated (but deterministic in the noise domain) measurement matrices that satisfy a generalized condition known as The Concentration of Measures Inequality. By this, we finally show that under our generalized assumptions, the Cramer-Rao bound of the estimation is achievable by using the typical estimator introduced in Babadi et al.