Submodular Maximization Through Barrier Functions

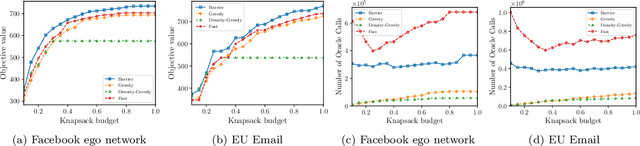
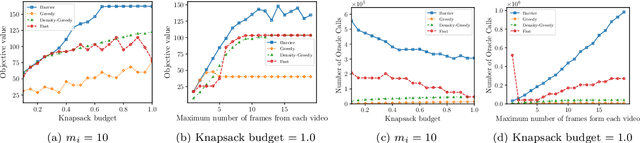
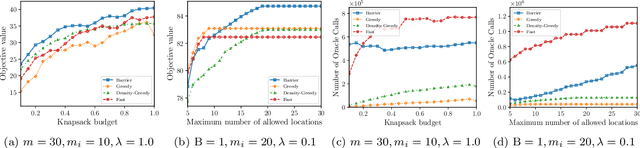
In this paper, we introduce a novel technique for constrained submodular maximization, inspired by barrier functions in continuous optimization. This connection not only improves the running time for constrained submodular maximization but also provides the state of the art guarantee. More precisely, for maximizing a monotone submodular function subject to the combination of a $k$-matchoid and $\ell$-knapsack constraint (for $\ell\leq k$), we propose a potential function that can be approximately minimized. Once we minimize the potential function up to an $\epsilon$ error it is guaranteed that we have found a feasible set with a $2(k+1+\epsilon)$-approximation factor which can indeed be further improved to $(k+1+\epsilon)$ by an enumeration technique. We extensively evaluate the performance of our proposed algorithm over several real-world applications, including a movie recommendation system, summarization tasks for YouTube videos, Twitter feeds and Yelp business locations, and a set cover problem.

High probability generalization bounds for uniformly stable algorithms with nearly optimal rate

Algorithmic stability is a classical approach to understanding and analysis of the generalization error of learning algorithms. A notable weakness of most stability-based generalization bounds is that they hold only in expectation. Generalization with high probability has been established in a landmark paper of Bousquet and Elisseeff (2002) albeit at the expense of an additional $\sqrt{n}$ factor in the bound. Specifically, their bound on the estimation error of any $\gamma$-uniformly stable learning algorithm on $n$ samples and range in $[0,1]$ is $O(\gamma \sqrt{n \log(1/\delta)} + \sqrt{\log(1/\delta)/n})$ with probability $\geq 1-\delta$. The $\sqrt{n}$ overhead makes the bound vacuous in the common settings where $\gamma \geq 1/\sqrt{n}$. A stronger bound was recently proved by the authors (Feldman and Vondrak, 2018) that reduces the overhead to at most $O(n^{1/4})$. Still, both of these results give optimal generalization bounds only when $\gamma = O(1/n)$. We prove a nearly tight bound of $O(\gamma \log(n)\log(n/\delta) + \sqrt{\log(1/\delta)/n})$ on the estimation error of any $\gamma$-uniformly stable algorithm. It implies that algorithms that are uniformly stable with $\gamma = O(1/\sqrt{n})$ have essentially the same estimation error as algorithms that output a fixed function. Our result leads to the first high-probability generalization bounds for multi-pass stochastic gradient descent and regularized ERM for stochastic convex problems with nearly optimal rate --- resolving open problems in prior work. Our proof technique is new and we introduce several analysis tools that might find additional applications.

Generalization Bounds for Uniformly Stable Algorithms

Uniform stability of a learning algorithm is a classical notion of algorithmic stability introduced to derive high-probability bounds on the generalization error (Bousquet and Elisseeff, 2002). Specifically, for a loss function with range bounded in $[0,1]$, the generalization error of $\gamma$-uniformly stable learning algorithm on $n$ samples is known to be at most $O((\gamma +1/n) \sqrt{n \log(1/\delta)})$ with probability at least $1-\delta$. Unfortunately, this bound does not lead to meaningful generalization bounds in many common settings where $\gamma \geq 1/\sqrt{n}$. At the same time the bound is known to be tight only when $\gamma = O(1/n)$. Here we prove substantially stronger generalization bounds for uniformly stable algorithms without any additional assumptions. First, we show that the generalization error in this setting is at most $O(\sqrt{(\gamma + 1/n) \log(1/\delta)})$ with probability at least $1-\delta$. In addition, we prove a tight bound of $O(\gamma^2 + 1/n)$ on the second moment of the generalization error. The best previous bound on the second moment of the generalization error is $O(\gamma + 1/n)$. Our proofs are based on new analysis techniques and our results imply substantially stronger generalization guarantees for several well-studied algorithms.

Tight Bounds on Low-degree Spectral Concentration of Submodular and XOS functions

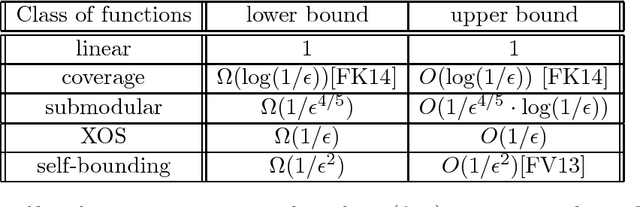
Submodular and fractionally subadditive (or equivalently XOS) functions play a fundamental role in combinatorial optimization, algorithmic game theory and machine learning. Motivated by learnability of these classes of functions from random examples, we consider the question of how well such functions can be approximated by low-degree polynomials in $\ell_2$ norm over the uniform distribution. This question is equivalent to understanding of the concentration of Fourier weight on low-degree coefficients, a central concept in Fourier analysis. We show that 1. For any submodular function $f:\{0,1\}^n \rightarrow [0,1]$, there is a polynomial of degree $O(\log (1/\epsilon) / \epsilon^{4/5})$ approximating $f$ within $\epsilon$ in $\ell_2$, and there is a submodular function that requires degree $\Omega(1/\epsilon^{4/5})$. 2. For any XOS function $f:\{0,1\}^n \rightarrow [0,1]$, there is a polynomial of degree $O(1/\epsilon)$ and there exists an XOS function that requires degree $\Omega(1/\epsilon)$. This improves on previous approaches that all showed an upper bound of $O(1/\epsilon^2)$ for submodular and XOS functions. The best previous lower bound was $\Omega(1/\epsilon^{2/3})$ for monotone submodular functions. Our techniques reveal new structural properties of submodular and XOS functions and the upper bounds lead to nearly optimal PAC learning algorithms for these classes of functions.

Optimal Bounds on Approximation of Submodular and XOS Functions by Juntas

We investigate the approximability of several classes of real-valued functions by functions of a small number of variables ({\em juntas}). Our main results are tight bounds on the number of variables required to approximate a function $f:\{0,1\}^n \rightarrow [0,1]$ within $\ell_2$-error $\epsilon$ over the uniform distribution: 1. If $f$ is submodular, then it is $\epsilon$-close to a function of $O(\frac{1}{\epsilon^2} \log \frac{1}{\epsilon})$ variables. This is an exponential improvement over previously known results. We note that $\Omega(\frac{1}{\epsilon^2})$ variables are necessary even for linear functions. 2. If $f$ is fractionally subadditive (XOS) it is $\epsilon$-close to a function of $2^{O(1/\epsilon^2)}$ variables. This result holds for all functions with low total $\ell_1$-influence and is a real-valued analogue of Friedgut's theorem for boolean functions. We show that $2^{\Omega(1/\epsilon)}$ variables are necessary even for XOS functions. As applications of these results, we provide learning algorithms over the uniform distribution. For XOS functions, we give a PAC learning algorithm that runs in time $2^{poly(1/\epsilon)} poly(n)$. For submodular functions we give an algorithm in the more demanding PMAC learning model (Balcan and Harvey, 2011) which requires a multiplicative $1+\gamma$ factor approximation with probability at least $1-\epsilon$ over the target distribution. Our uniform distribution algorithm runs in time $2^{poly(1/(\gamma\epsilon))} poly(n)$. This is the first algorithm in the PMAC model that over the uniform distribution can achieve a constant approximation factor arbitrarily close to 1 for all submodular functions. As follows from the lower bounds in (Feldman et al., 2013) both of these algorithms are close to optimal. We also give applications for proper learning, testing and agnostic learning with value queries of these classes.

Lazier Than Lazy Greedy

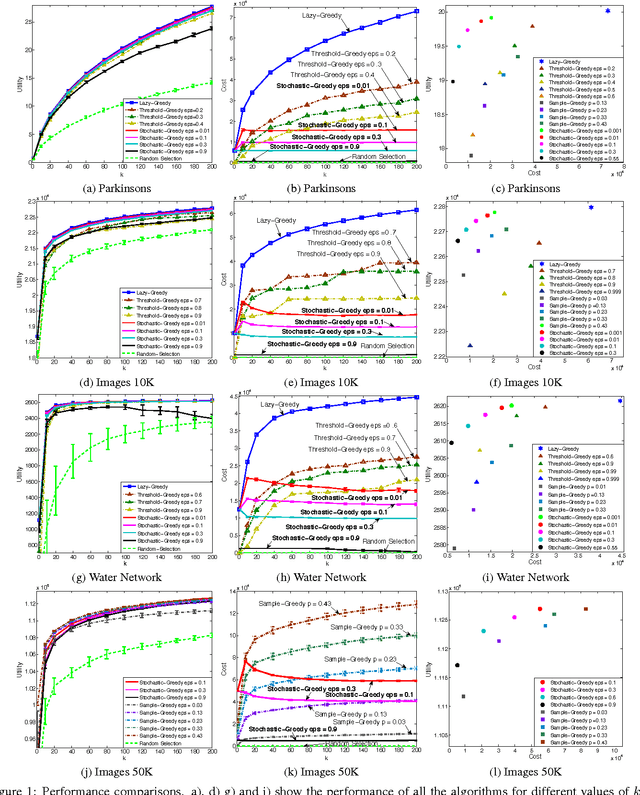
Is it possible to maximize a monotone submodular function faster than the widely used lazy greedy algorithm (also known as accelerated greedy), both in theory and practice? In this paper, we develop the first linear-time algorithm for maximizing a general monotone submodular function subject to a cardinality constraint. We show that our randomized algorithm, STOCHASTIC-GREEDY, can achieve a $(1-1/e-\varepsilon)$ approximation guarantee, in expectation, to the optimum solution in time linear in the size of the data and independent of the cardinality constraint. We empirically demonstrate the effectiveness of our algorithm on submodular functions arising in data summarization, including training large-scale kernel methods, exemplar-based clustering, and sensor placement. We observe that STOCHASTIC-GREEDY practically achieves the same utility value as lazy greedy but runs much faster. More surprisingly, we observe that in many practical scenarios STOCHASTIC-GREEDY does not evaluate the whole fraction of data points even once and still achieves indistinguishable results compared to lazy greedy.

Representation, Approximation and Learning of Submodular Functions Using Low-rank Decision Trees

We study the complexity of approximate representation and learning of submodular functions over the uniform distribution on the Boolean hypercube $\{0,1\}^n$. Our main result is the following structural theorem: any submodular function is $\epsilon$-close in $\ell_2$ to a real-valued decision tree (DT) of depth $O(1/\epsilon^2)$. This immediately implies that any submodular function is $\epsilon$-close to a function of at most $2^{O(1/\epsilon^2)}$ variables and has a spectral $\ell_1$ norm of $2^{O(1/\epsilon^2)}$. It also implies the closest previous result that states that submodular functions can be approximated by polynomials of degree $O(1/\epsilon^2)$ (Cheraghchi et al., 2012). Our result is proved by constructing an approximation of a submodular function by a DT of rank $4/\epsilon^2$ and a proof that any rank-$r$ DT can be $\epsilon$-approximated by a DT of depth $\frac{5}{2}(r+\log(1/\epsilon))$. We show that these structural results can be exploited to give an attribute-efficient PAC learning algorithm for submodular functions running in time $\tilde{O}(n^2) \cdot 2^{O(1/\epsilon^{4})}$. The best previous algorithm for the problem requires $n^{O(1/\epsilon^{2})}$ time and examples (Cheraghchi et al., 2012) but works also in the agnostic setting. In addition, we give improved learning algorithms for a number of related settings. We also prove that our PAC and agnostic learning algorithms are essentially optimal via two lower bounds: (1) an information-theoretic lower bound of $2^{\Omega(1/\epsilon^{2/3})}$ on the complexity of learning monotone submodular functions in any reasonable model; (2) computational lower bound of $n^{\Omega(1/\epsilon^{2/3})}$ based on a reduction to learning of sparse parities with noise, widely-believed to be intractable. These are the first lower bounds for learning of submodular functions over the uniform distribution.