ATLANTIS: AI-driven Threat Localization, Analysis, and Triage Intelligence System

We present ATLANTIS, the cyber reasoning system developed by Team Atlanta that won 1st place in the Final Competition of DARPA's AI Cyber Challenge (AIxCC) at DEF CON 33 (August 2025). AIxCC (2023-2025) challenged teams to build autonomous cyber reasoning systems capable of discovering and patching vulnerabilities at the speed and scale of modern software. ATLANTIS integrates large language models (LLMs) with program analysis -- combining symbolic execution, directed fuzzing, and static analysis -- to address limitations in automated vulnerability discovery and program repair. Developed by researchers at Georgia Institute of Technology, Samsung Research, KAIST, and POSTECH, the system addresses core challenges: scaling across diverse codebases from C to Java, achieving high precision while maintaining broad coverage, and producing semantically correct patches that preserve intended behavior. We detail the design philosophy, architectural decisions, and implementation strategies behind ATLANTIS, share lessons learned from pushing the boundaries of automated security when program analysis meets modern AI, and release artifacts to support reproducibility and future research.

PnP for Two-Dimensional Pose Estimation

We propose a PnP algorithm for a camera constrained to two-dimensional movement (applicable, for instance, to many wheeled robotics platforms). Leveraging this assumption allows performance improvements over 3D PnP algorithms due to the reduction in search space dimensionality. It also reduces the incidence of ambiguous pose estimates (as, in most cases, the spurious solutions fall outside the plane of movement). Our algorithm finds an approximate solution using geometric criteria and refines its prediction iteratively. We compare this algorithm to existing 3D PnP algorithms in terms of accuracy, performance, and robustness to noise.

Margin-Independent Online Multiclass Learning via Convex Geometry

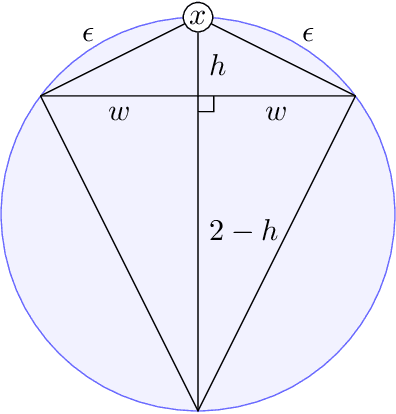
We consider the problem of multi-class classification, where a stream of adversarially chosen queries arrive and must be assigned a label online. Unlike traditional bounds which seek to minimize the misclassification rate, we minimize the total distance from each query to the region corresponding to its correct label. When the true labels are determined via a nearest neighbor partition -- i.e. the label of a point is given by which of $k$ centers it is closest to in Euclidean distance -- we show that one can achieve a loss that is independent of the total number of queries. We complement this result by showing that learning general convex sets requires an almost linear loss per query. Our results build off of regret guarantees for the geometric problem of contextual search. In addition, we develop a novel reduction technique from multiclass classification to binary classification which may be of independent interest.

Online Learning via Offline Greedy Algorithms: Applications in Market Design and Optimization

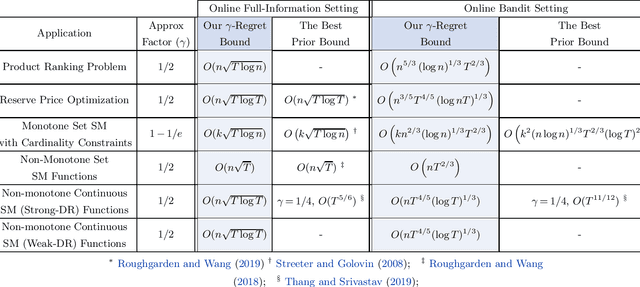
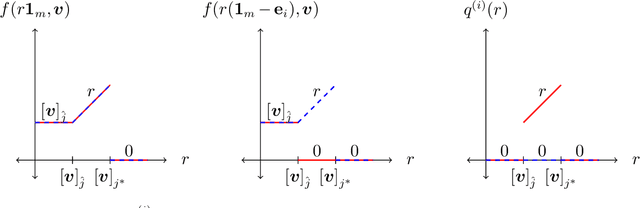
Motivated by online decision-making in time-varying combinatorial environments, we study the problem of transforming offline algorithms to their online counterparts. We focus on offline combinatorial problems that are amenable to a constant factor approximation using a greedy algorithm that is robust to local errors. For such problems, we provide a general framework that efficiently transforms offline robust greedy algorithms to online ones using Blackwell approachability. We show that the resulting online algorithms have $O(\sqrt{T})$ (approximate) regret under the full information setting. We further introduce a bandit extension of Blackwell approachability that we call Bandit Blackwell approachability. We leverage this notion to transform greedy robust offline algorithms into a $O(T^{2/3})$ (approximate) regret in the bandit setting. Demonstrating the flexibility of our framework, we apply our offline-to-online transformation to several problems at the intersection of revenue management, market design, and online optimization, including product ranking optimization in online platforms, reserve price optimization in auctions, and submodular maximization. We show that our transformation, when applied to these applications, leads to new regret bounds or improves the current known bounds.