Alekh Agarwal
Safe Reinforcement Learning via Curriculum Induction
Jun 22, 2020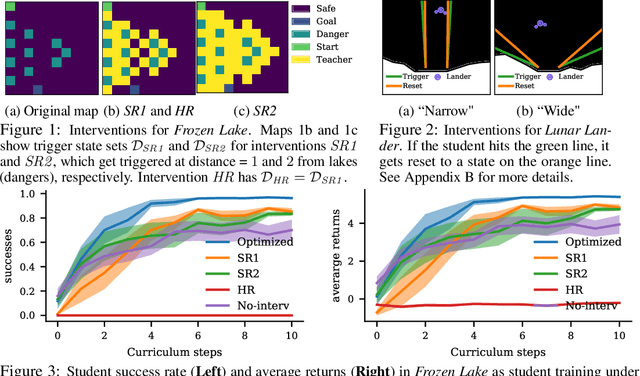


Abstract:In safety-critical applications, autonomous agents may need to learn in an environment where mistakes can be very costly. In such settings, the agent needs to behave safely not only after but also while learning. To achieve this, existing safe reinforcement learning methods make an agent rely on priors that let it avoid dangerous situations during exploration with high probability, but both the probabilistic guarantees and the smoothness assumptions inherent in the priors are not viable in many scenarios of interest such as autonomous driving. This paper presents an alternative approach inspired by human teaching, where an agent learns under the supervision of an automatic instructor that saves the agent from violating constraints during learning. In this model, we introduce the monitor that neither needs to know how to do well at the task the agent is learning nor needs to know how the environment works. Instead, it has a library of reset controllers that it activates when the agent starts behaving dangerously, preventing it from doing damage. Crucially, the choices of which reset controller to apply in which situation affect the speed of agent learning. Based on observing agents' progress, the teacher itself learns a policy for choosing the reset controllers, a curriculum, to optimize the agent's final policy reward. Our experiments use this framework in two environments to induce curricula for safe and efficient learning.
Optimizing Interactive Systems via Data-Driven Objectives
Jun 19, 2020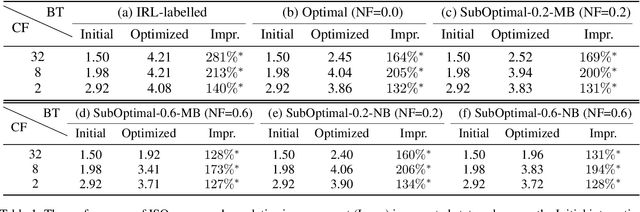
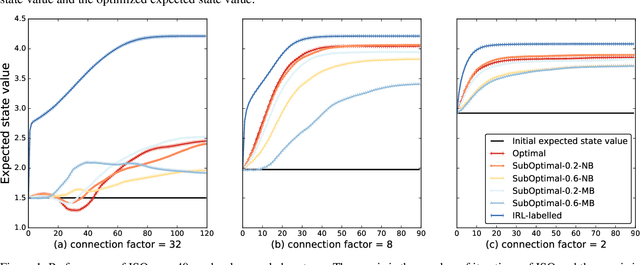
Abstract:Effective optimization is essential for real-world interactive systems to provide a satisfactory user experience in response to changing user behavior. However, it is often challenging to find an objective to optimize for interactive systems (e.g., policy learning in task-oriented dialog systems). Generally, such objectives are manually crafted and rarely capture complex user needs in an accurate manner. We propose an approach that infers the objective directly from observed user interactions. These inferences can be made regardless of prior knowledge and across different types of user behavior. We introduce Interactive System Optimizer (ISO), a novel algorithm that uses these inferred objectives for optimization. Our main contribution is a new general principled approach to optimizing interactive systems using data-driven objectives. We demonstrate the high effectiveness of ISO over several simulations.
FLAMBE: Structural Complexity and Representation Learning of Low Rank MDPs
Jun 18, 2020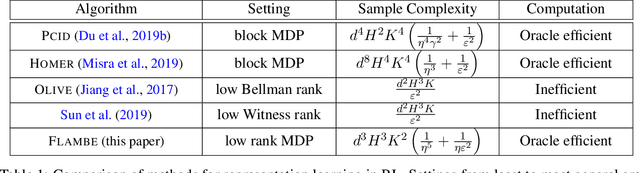
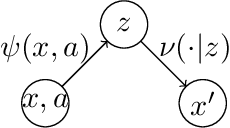

Abstract:In order to deal with the curse of dimensionality in reinforcement learning (RL), it is common practice to make parametric assumptions where values or policies are functions of some low dimensional feature space. This work focuses on the representation learning question: how can we learn such features? Under the assumption that the underlying (unknown) dynamics correspond to a low rank transition matrix, we show how the representation learning question is related to a particular non-linear matrix decomposition problem. Structurally, we make precise connections between these low rank MDPs and latent variable models, showing how they significantly generalize prior formulations for representation learning in RL. Algorithmically, we develop FLAMBE, which engages in exploration and representation learning for provably efficient RL in low rank transition models.
Reparameterized Variational Divergence Minimization for Stable Imitation
Jun 18, 2020

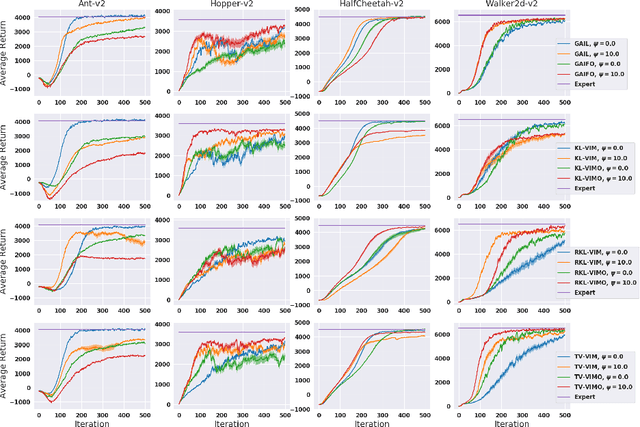
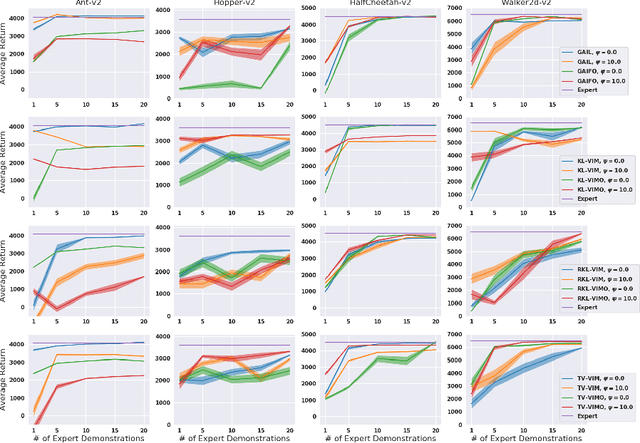
Abstract:While recent state-of-the-art results for adversarial imitation-learning algorithms are encouraging, recent works exploring the imitation learning from observation (ILO) setting, where trajectories \textit{only} contain expert observations, have not been met with the same success. Inspired by recent investigations of $f$-divergence manipulation for the standard imitation learning setting(Ke et al., 2019; Ghasemipour et al., 2019), we here examine the extent to which variations in the choice of probabilistic divergence may yield more performant ILO algorithms. We unfortunately find that $f$-divergence minimization through reinforcement learning is susceptible to numerical instabilities. We contribute a reparameterization trick for adversarial imitation learning to alleviate the optimization challenges of the promising $f$-divergence minimization framework. Empirically, we demonstrate that our design choices allow for ILO algorithms that outperform baseline approaches and more closely match expert performance in low-dimensional continuous-control tasks.
Federated Residual Learning
Mar 28, 2020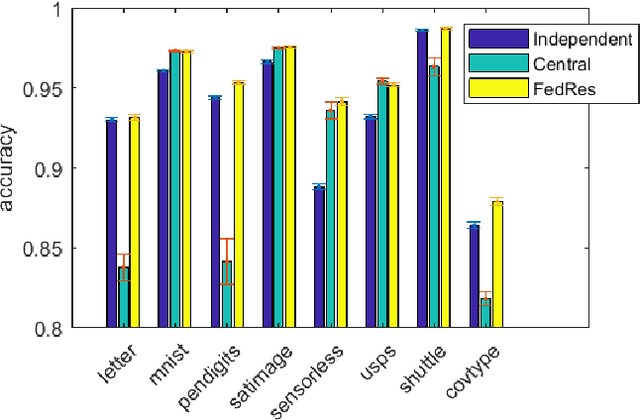
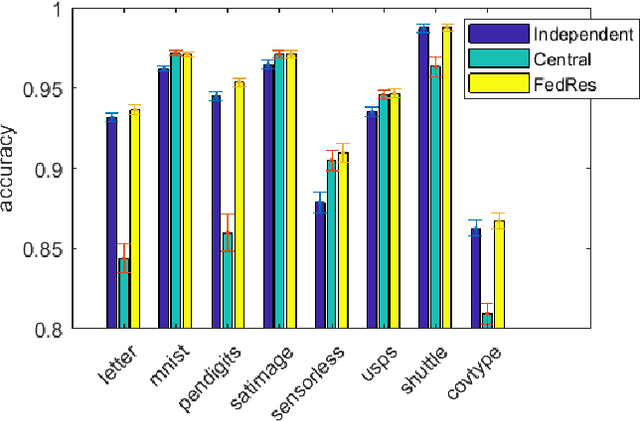
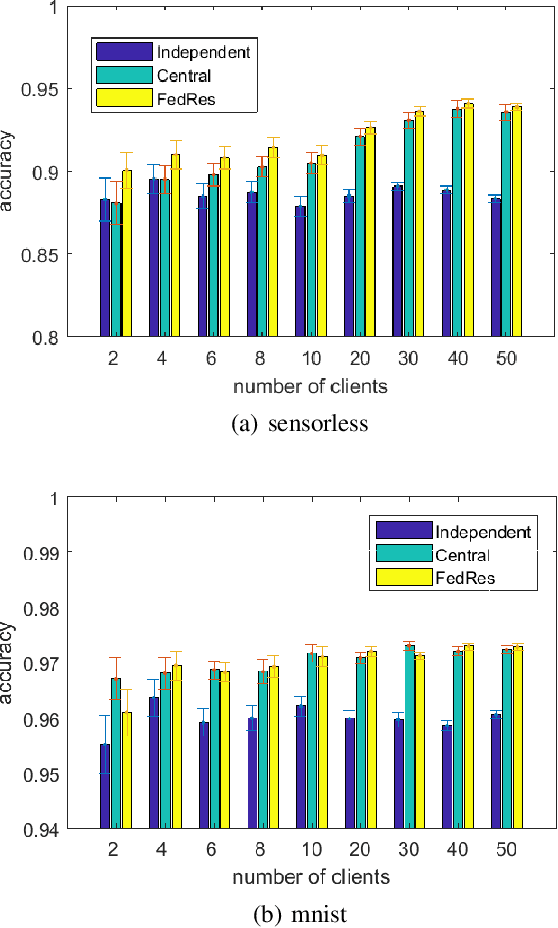
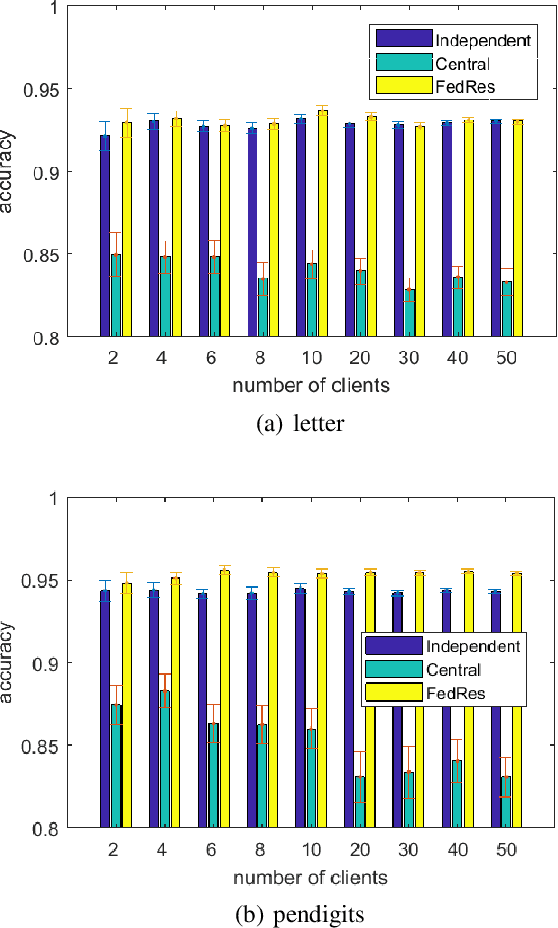
Abstract:We study a new form of federated learning where the clients train personalized local models and make predictions jointly with the server-side shared model. Using this new federated learning framework, the complexity of the central shared model can be minimized while still gaining all the performance benefits that joint training provides. Our framework is robust to data heterogeneity, addressing the slow convergence problem traditional federated learning methods face when the data is non-i.i.d. across clients. We test the theory empirically and find substantial performance gains over baselines.
Taking a hint: How to leverage loss predictors in contextual bandits?
Mar 04, 2020

Abstract:We initiate the study of learning in contextual bandits with the help of loss predictors. The main question we address is whether one can improve over the minimax regret $\mathcal{O}(\sqrt{T})$ for learning over $T$ rounds, when the total error of the predictor $\mathcal{E} \leq T$ is relatively small. We provide a complete answer to this question, including upper and lower bounds for various settings: adversarial versus stochastic environments, known versus unknown $\mathcal{E}$, and single versus multiple predictors. We show several surprising results, such as 1) the optimal regret is $\mathcal{O}(\min\{\sqrt{T}, \sqrt{\mathcal{E}}T^\frac{1}{4}\})$ when $\mathcal{E}$ is known, a sharp contrast to the standard and better bound $\mathcal{O}(\sqrt{\mathcal{E}})$ for non-contextual problems (such as multi-armed bandits); 2) the same bound cannot be achieved if $\mathcal{E}$ is unknown, but as a remedy, $\mathcal{O}(\sqrt{\mathcal{E}}T^\frac{1}{3})$ is achievable; 3) with $M$ predictors, a linear dependence on $M$ is necessary, even if logarithmic dependence is possible for non-contextual problems. We also develop several novel algorithmic techniques to achieve matching upper bounds, including 1) a key action remapping technique for optimal regret with known $\mathcal{E}$, 2) implementing Catoni's robust mean estimator efficiently via an ERM oracle leading to an efficient algorithm in the stochastic setting with optimal regret, 3) constructing an underestimator for $\mathcal{E}$ via estimating the histogram with bins of exponentially increasing size for the stochastic setting with unknown $\mathcal{E}$, and 4) a self-referential scheme for learning with multiple predictors, all of which might be of independent interest.
Optimality and Approximation with Policy Gradient Methods in Markov Decision Processes
Aug 29, 2019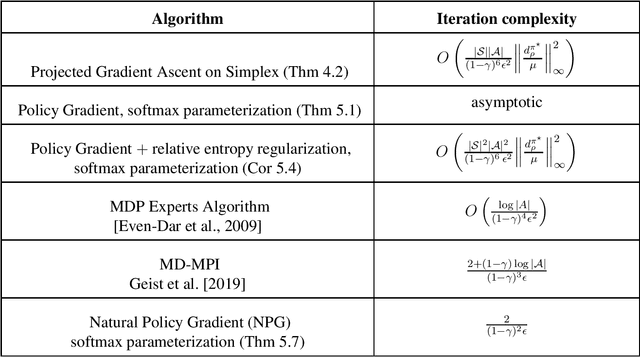
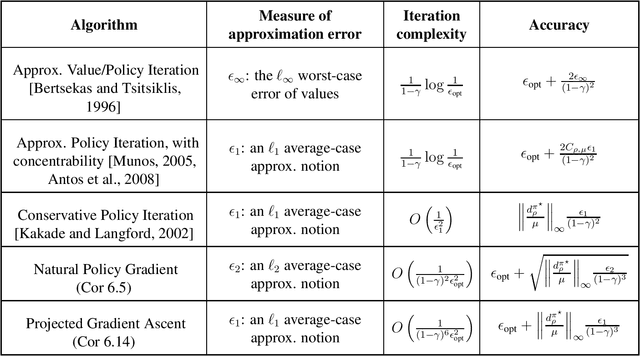
Abstract:Policy gradient methods are among the most effective methods in challenging reinforcement learning problems with large state and/or action spaces. However, little is known about even their most basic theoretical convergence properties, including: if and how fast they converge to a globally optimal solution (say with a sufficiently rich policy class); how they cope with approximation error due to using a restricted class of parametric policies; or their finite sample behavior. Such characterizations are important not only to compare these methods to their approximate value function counterparts (where such issues are relatively well understood, at least in the worst case), but also to help with more principled approaches to algorithm design. This work provides provable characterizations of computational, approximation, and sample size issues with regards to policy gradient methods in the context of discounted Markov Decision Processes (MDPs). We focus on both: 1) "tabular" policy parameterizations, where the optimal policy is contained in the class and where we show global convergence to the optimal policy, and 2) restricted policy classes, which may not contain the optimal policy and where we provide agnostic learning results. One insight of this work is in formalizing the importance how a favorable initial state distribution provides a means to circumvent worst-case exploration issues. Overall, these results place policy gradient methods under a solid theoretical footing, analogous to the global convergence guarantees of iterative value function based algorithms.
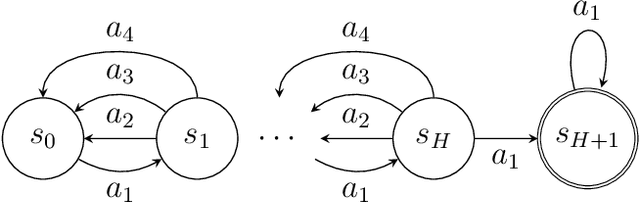
On the Optimality of Sparse Model-Based Planning for Markov Decision Processes
Jul 04, 2019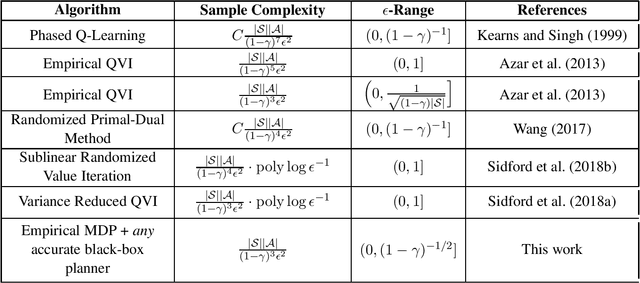
Abstract:This work considers the sample complexity of obtaining an $\epsilon$-optimal policy in a discounted Markov Decision Process (MDP), given only access to a generative model. In this model, the learner accesses the underlying transition model via a sampling oracle that provides a sample of the next state, when given any state-action pair as input. In this work, we study the effectiveness of the most natural plug-in approach to model-based planning: we build the maximum likelihood estimate of the transition model in the MDP from observations and then find an optimal policy in this empirical MDP. We ask arguably the most basic and unresolved question in model-based planning: is the na\"ive "plug-in" approach, non-asymptotically, minimax optimal in the quality of the policy it finds, given a fixed sample size? With access to a generative model, we resolve this question in the strongest possible sense: our main result shows that \emph{any} high accuracy solution in the plug-in model constructed with $N$ samples, provides an $\epsilon$-optimal policy in the true underlying MDP. In comparison, all prior (non-asymptotically) minimax optimal results use model-free approaches, such as the Variance Reduced Q-value iteration algorithm (Sidford et al 2018), while the best known model-based results (e.g. Azar et al 2013) require larger sample sample sizes in their dependence on the planning horizon or the state space. Notably, we show that the model-based approach allows the use of \emph{any} efficient planning algorithm in the empirical MDP, which simplifies the algorithm design as this approach does not tie the algorithm to the sampling procedure. The core of our analysis is a novel "absorbing MDP" construction to address the statistical dependency issues that arise in the analysis of model-based planning approaches, a construction which may be helpful more generally.
Bias Correction of Learned Generative Models using Likelihood-Free Importance Weighting
Jun 23, 2019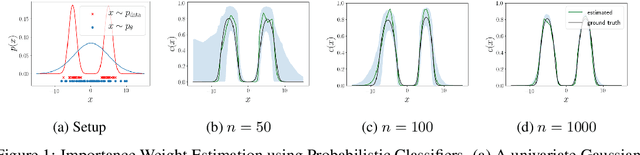

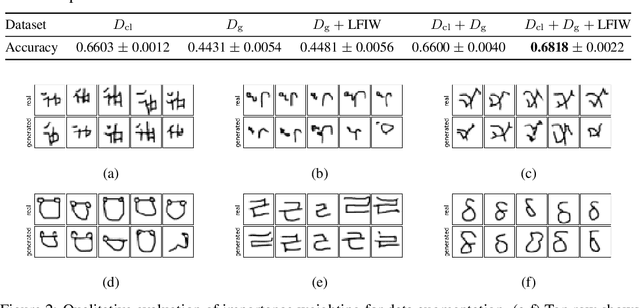
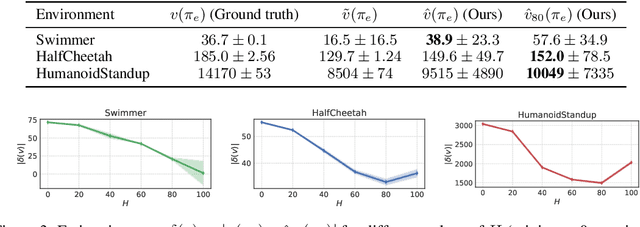
Abstract:A learned generative model often produces biased statistics relative to the underlying data distribution. A standard technique to correct this bias is importance sampling, where samples from the model are weighted by the likelihood ratio under model and true distributions. When the likelihood ratio is unknown, it can be estimated by training a probabilistic classifier to distinguish samples from the two distributions. In this paper, we employ this likelihood-free importance weighting framework to correct for the bias in state-of-the-art deep generative models. We find that this technique consistently improves standard goodness-of-fit metrics for evaluating the sample quality of state-of-the-art generative models, suggesting reduced bias. Finally, we demonstrate its utility on representative applications in a) data augmentation for classification using generative adversarial networks, and b) model-based policy evaluation using off-policy data.
Deep Batch Active Learning by Diverse, Uncertain Gradient Lower Bounds
Jun 09, 2019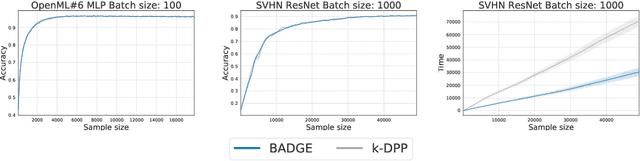
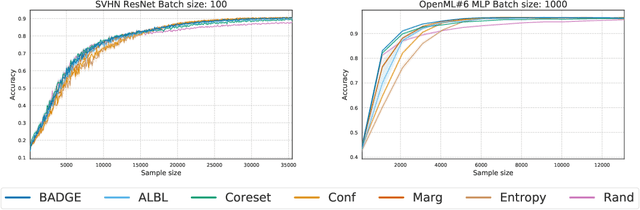
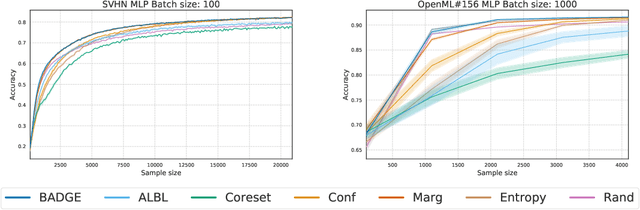
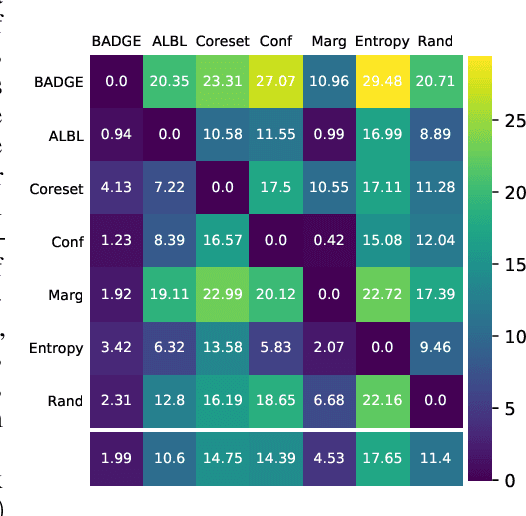
Abstract:We design a new algorithm for batch active learning with deep neural network models. Our algorithm, Batch Active learning by Diverse Gradient Embeddings (BADGE), samples groups of points that are disparate and high-magnitude when represented in a hallucinated gradient space, a strategy designed to incorporate both predictive uncertainty and sample diversity into every selected batch. Crucially, BADGE trades off between diversity and uncertainty without requiring any hand-tuned hyperparameters. We show that while other approaches sometimes succeed for particular batch sizes or architectures, BADGE consistently performs as well or better, making it a versatile option for practical active learning problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge