Dynamic Triangulation-Based Graph Rewiring for Graph Neural Networks

Graph Neural Networks (GNNs) have emerged as the leading paradigm for learning over graph-structured data. However, their performance is limited by issues inherent to graph topology, most notably oversquashing and oversmoothing. Recent advances in graph rewiring aim to mitigate these limitations by modifying the graph topology to promote more effective information propagation. In this work, we introduce TRIGON, a novel framework that constructs enriched, non-planar triangulations by learning to select relevant triangles from multiple graph views. By jointly optimizing triangle selection and downstream classification performance, our method produces a rewired graph with markedly improved structural properties such as reduced diameter, increased spectral gap, and lower effective resistance compared to existing rewiring methods. Empirical results demonstrate that TRIGON outperforms state-of-the-art approaches on node classification tasks across a range of homophilic and heterophilic benchmarks.

DuoGNN: Topology-aware Graph Neural Network with Homophily and Heterophily Interaction-Decoupling

Graph Neural Networks (GNNs) have proven effective in various medical imaging applications, such as automated disease diagnosis. However, due to the local neighborhood aggregation paradigm in message passing which characterizes these models, they inherently suffer from two fundamental limitations: first, indistinguishable node embeddings due to heterophilic node aggregation (known as over-smoothing), and second, impaired message passing due to aggregation through graph bottlenecks (known as over-squashing). These challenges hinder the model expressiveness and prevent us from using deeper models to capture long-range node dependencies within the graph. Popular solutions in the literature are either too expensive to process large graphs due to high time complexity or do not generalize across all graph topologies. To address these limitations, we propose DuoGNN, a scalable and generalizable architecture which leverages topology to decouple homophilic and heterophilic edges and capture both short-range and long-range interactions. Our three core contributions introduce (i) a topological edge-filtering algorithm which extracts homophilic interactions and enables the model to generalize well for any graph topology, (ii) a heterophilic graph condensation technique which extracts heterophilic interactions and ensures scalability, and (iii) a dual homophilic and heterophilic aggregation pipeline which prevents over-smoothing and over-squashing during the message passing. We benchmark our model on medical and non-medical node classification datasets and compare it with its variants, showing consistent improvements across all tasks. Our DuoGNN code is available at https://github.com/basiralab/DuoGNN.

Self-Directed Learning of Convex Labelings on Graphs

We study the problem of learning the clusters of a given graph in the self-directed learning setup. This learning setting is a variant of online learning, where rather than an adversary determining the sequence in which nodes are presented, the learner autonomously and adaptively selects them. While self-directed learning of Euclidean halfspaces, linear functions, and general abstract multi-class hypothesis classes was recently considered, no results previously existed specifically for self-directed node classification on graphs. In this paper, we address this problem developing efficient algorithms for it. More specifically, we focus on the case of (geodesically) convex clusters, i.e., for every two nodes sharing the same label, all nodes on every shortest path between them also share the same label. In particular, we devise a polynomial-time algorithm that makes only $3(h(G)+1)^4 \ln n$ mistakes on graphs with two convex clusters, where $n$ is the total number of nodes and $h(G)$ is the Hadwiger number, i.e., the size of the largest clique minor of the graph $G$. We also show that our algorithm is robust to the case that clusters are slightly non-convex, still achieving a mistake bound logarithmic in $n$. Finally, for the more standard case of homophilic clusters, where strongly connected nodes tend to belong the same class, we devise a simple and efficient algorithm.

AdaFGL: A New Paradigm for Federated Node Classification with Topology Heterogeneity

Recently, Federated Graph Learning (FGL) has attracted significant attention as a distributed framework based on graph neural networks, primarily due to its capability to break data silos. Existing FGL studies employ community split on the homophilous global graph by default to simulate federated semi-supervised node classification settings. Such a strategy assumes the consistency of topology between the multi-client subgraphs and the global graph, where connected nodes are highly likely to possess similar feature distributions and the same label. However, in real-world implementations, the varying perspectives of local data engineering result in various subgraph topologies, posing unique heterogeneity challenges in FGL. Unlike the well-known label Non-independent identical distribution (Non-iid) problems in federated learning, FGL heterogeneity essentially reveals the topological divergence among multiple clients, namely homophily or heterophily. To simulate and handle this unique challenge, we introduce the concept of structure Non-iid split and then present a new paradigm called \underline{Ada}ptive \underline{F}ederated \underline{G}raph \underline{L}earning (AdaFGL), a decoupled two-step personalized approach. To begin with, AdaFGL employs standard multi-client federated collaborative training to acquire the federated knowledge extractor by aggregating uploaded models in the final round at the server. Then, each client conducts personalized training based on the local subgraph and the federated knowledge extractor. Extensive experiments on the 12 graph benchmark datasets validate the superior performance of AdaFGL over state-of-the-art baselines. Specifically, in terms of test accuracy, our proposed AdaFGL outperforms baselines by significant margins of 3.24\% and 5.57\% on community split and structure Non-iid split, respectively.

Graph Polynomial Convolution Models for Node Classification of Non-Homophilous Graphs

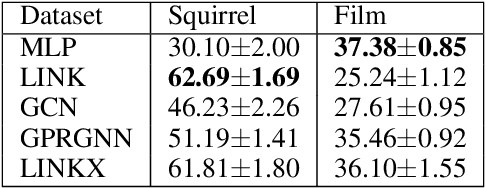
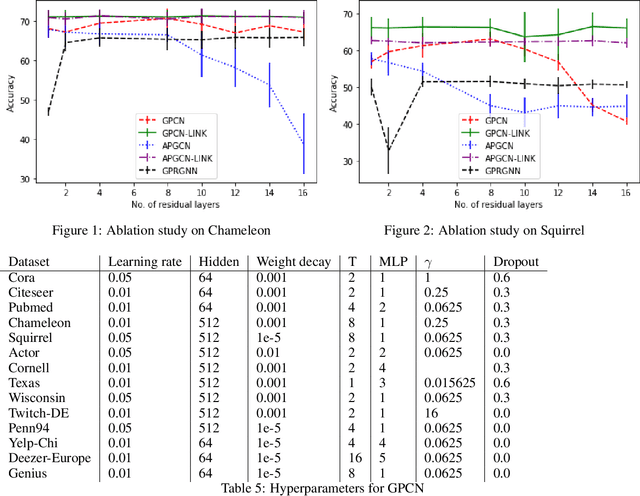
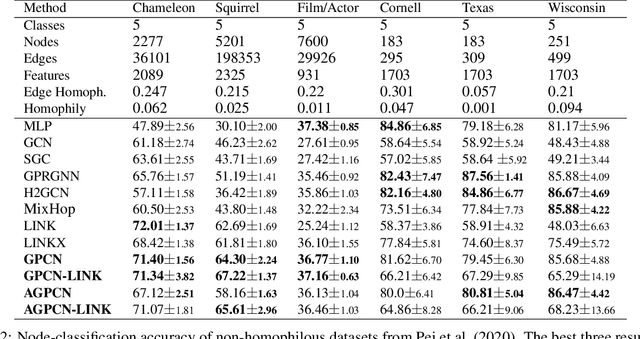
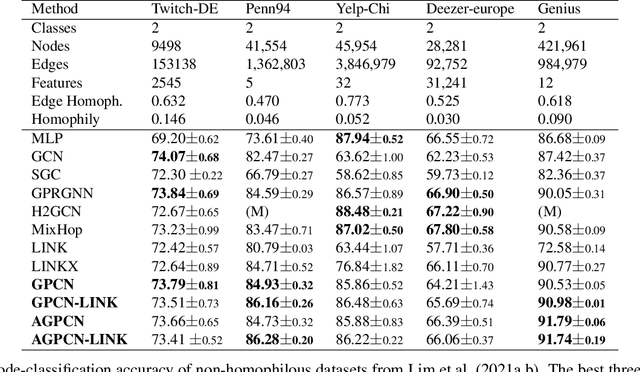
We investigate efficient learning from higher-order graph convolution and learning directly from adjacency matrices for node classification. We revisit the scaled graph residual network and remove ReLU activation from residual layers and apply a single weight matrix at each residual layer. We show that the resulting model lead to new graph convolution models as a polynomial of the normalized adjacency matrix, the residual weight matrix, and the residual scaling parameter. Additionally, we propose adaptive learning between directly graph polynomial convolution models and learning directly from the adjacency matrix. Furthermore, we propose fully adaptive models to learn scaling parameters at each residual layer. We show that generalization bounds of proposed methods are bounded as a polynomial of eigenvalue spectrum, scaling parameters, and upper bounds of residual weights. By theoretical analysis, we argue that the proposed models can obtain improved generalization bounds by limiting the higher-orders of convolutions and direct learning from the adjacency matrix. Using a wide set of real-data, we demonstrate that the proposed methods obtain improved accuracy for node-classification of non-homophilous graphs.

Demystifying Structural Disparity in Graph Neural Networks: Can One Size Fit All?

Recent studies on Graph Neural Networks(GNNs) provide both empirical and theoretical evidence supporting their effectiveness in capturing structural patterns on both homophilic and certain heterophilic graphs. Notably, most real-world homophilic and heterophilic graphs are comprised of a mixture of nodes in both homophilic and heterophilic structural patterns, exhibiting a structural disparity. However, the analysis of GNN performance with respect to nodes exhibiting different structural patterns, e.g., homophilic nodes in heterophilic graphs, remains rather limited. In the present study, we provide evidence that Graph Neural Networks(GNNs) on node classification typically perform admirably on homophilic nodes within homophilic graphs and heterophilic nodes within heterophilic graphs while struggling on the opposite node set, exhibiting a performance disparity. We theoretically and empirically identify effects of GNNs on testing nodes exhibiting distinct structural patterns. We then propose a rigorous, non-i.i.d PAC-Bayesian generalization bound for GNNs, revealing reasons for the performance disparity, namely the aggregated feature distance and homophily ratio difference between training and testing nodes. Furthermore, we demonstrate the practical implications of our new findings via (1) elucidating the effectiveness of deeper GNNs; and (2) revealing an over-looked distribution shift factor on graph out-of-distribution problem and proposing a new scenario accordingly.

Characterizing Graph Datasets for Node Classification: Beyond Homophily-Heterophily Dichotomy

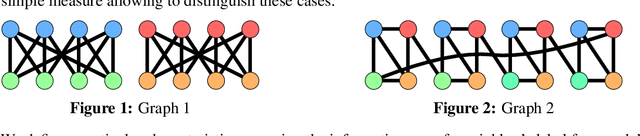
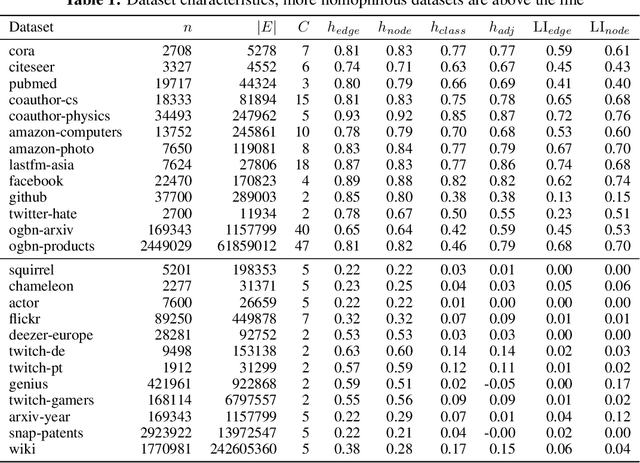
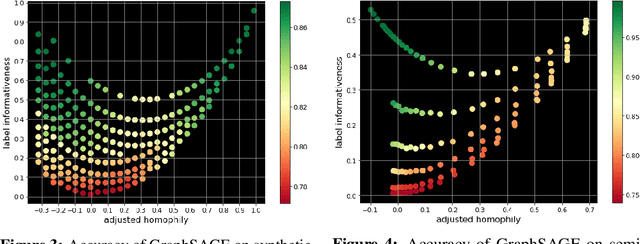
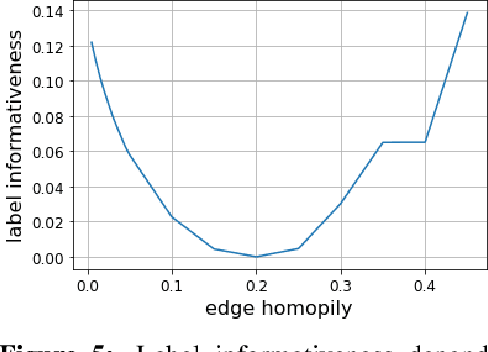
Homophily is a graph property describing the tendency of edges to connect similar nodes; the opposite is called heterophily. While homophily is natural for many real-world networks, there are also networks without this property. It is often believed that standard message-passing graph neural networks (GNNs) do not perform well on non-homophilous graphs, and thus such datasets need special attention. While a lot of effort has been put into developing graph representation learning methods for heterophilous graphs, there is no universally agreed upon measure of homophily. Several metrics for measuring homophily have been used in the literature, however, we show that all of them have critical drawbacks preventing comparison of homophily levels between different datasets. We formalize desirable properties for a proper homophily measure and show how existing literature on the properties of classification performance metrics can be linked to our problem. In doing so we find a measure that we call adjusted homophily that satisfies more desirable properties than existing homophily measures. Interestingly, this measure is related to two classification performance metrics - Cohen's Kappa and Matthews correlation coefficient. Then, we go beyond the homophily-heterophily dichotomy and propose a new property that we call label informativeness (LI) that characterizes how much information a neighbor's label provides about a node's label. We theoretically show that LI is comparable across datasets with different numbers of classes and class size balance. Through a series of experiments we show that LI is a better predictor of the performance of GNNs on a dataset than homophily. We show that LI explains why GNNs can sometimes perform well on heterophilous datasets - a phenomenon recently observed in the literature.

Alleviating neighbor bias: augmenting graph self-supervise learning with structural equivalent positive samples

In recent years, using a self-supervised learning framework to learn the general characteristics of graphs has been considered a promising paradigm for graph representation learning. The core of self-supervised learning strategies for graph neural networks lies in constructing suitable positive sample selection strategies. However, existing GNNs typically aggregate information from neighboring nodes to update node representations, leading to an over-reliance on neighboring positive samples, i.e., homophilous samples; while ignoring long-range positive samples, i.e., positive samples that are far apart on the graph but structurally equivalent samples, a problem we call "neighbor bias." This neighbor bias can reduce the generalization performance of GNNs. In this paper, we argue that the generalization properties of GNNs should be determined by combining homogeneous samples and structurally equivalent samples, which we call the "GC combination hypothesis." Therefore, we propose a topological signal-driven self-supervised method. It uses a topological information-guided structural equivalence sampling strategy. First, we extract multiscale topological features using persistent homology. Then we compute the structural equivalence of node pairs based on their topological features. In particular, we design a topological loss function to pull in non-neighboring node pairs with high structural equivalence in the representation space to alleviate neighbor bias. Finally, we use the joint training mechanism to adjust the effect of structural equivalence on the model to fit datasets with different characteristics. We conducted experiments on the node classification task across seven graph datasets. The results show that the model performance can be effectively improved using a strategy of topological signal enhancement.

Simplified Graph Convolution with Heterophily

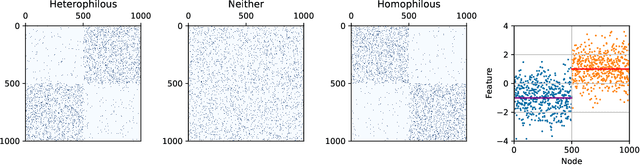
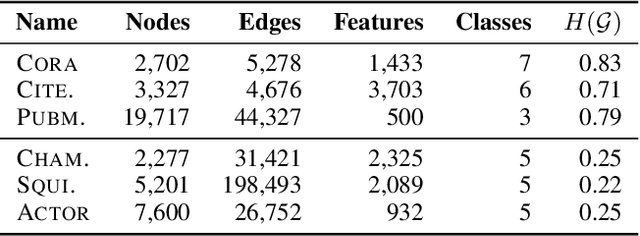
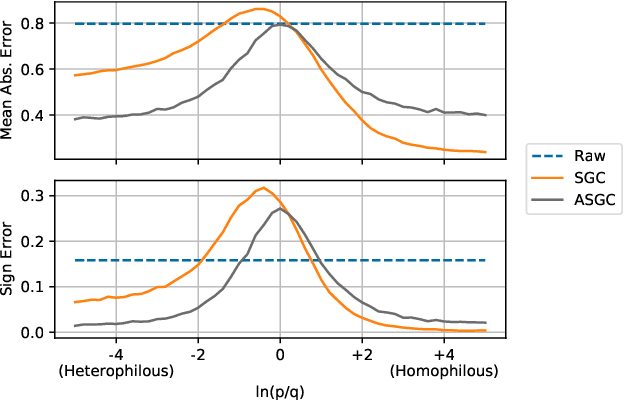
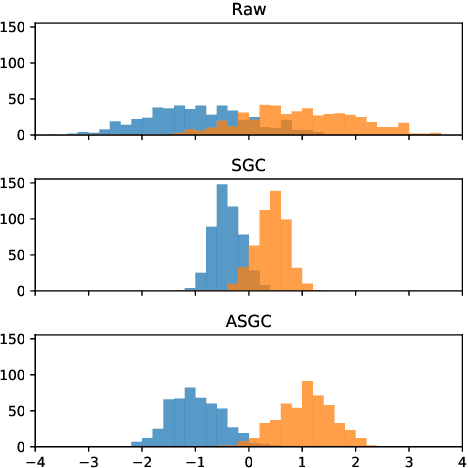
Graph convolutional networks (GCNs) (Kipf & Welling, 2017) attempt to extend the success of deep learning in modeling image and text data to graphs. However, like other deep models, GCNs comprise repeated nonlinear transformations of inputs and are therefore time and memory intensive to train. Recent work has shown that a much simpler and faster model, Simple Graph Convolution (SGC) (Wu et al., 2019), is competitive with GCNs in common graph machine learning benchmarks. The use of graph data in SGC implicitly assumes the common but not universal graph characteristic of homophily, wherein nodes link to nodes which are similar. Here we show that SGC is indeed ineffective for heterophilous (i.e., non-homophilous) graphs via experiments on synthetic and real-world datasets. We propose Adaptive Simple Graph Convolution (ASGC), which we show can adapt to both homophilous and heterophilous graph structure. Like SGC, ASGC is not a deep model, and hence is fast, scalable, and interpretable. We find that our non-deep method often outperforms state-of-the-art deep models at node classification on a benchmark of real-world datasets. The SGC paper questioned whether the complexity of graph neural networks is warranted for common graph problems involving homophilous networks; our results suggest that this question is still open even for more complicated problems involving heterophilous networks.

Graph Posterior Network: Bayesian Predictive Uncertainty for Node Classification

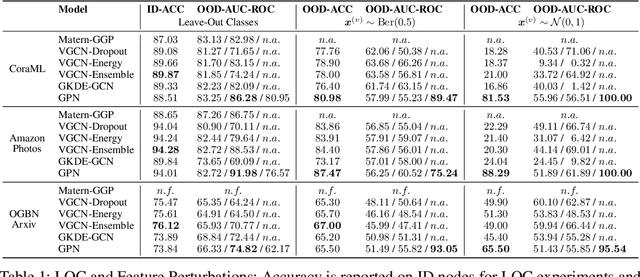
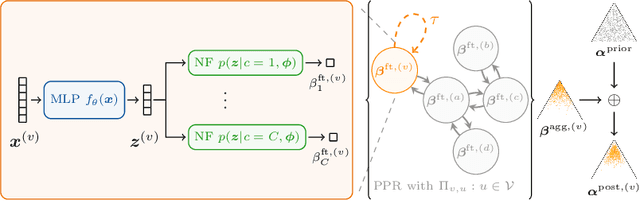
The interdependence between nodes in graphs is key to improve class predictions on nodes and utilized in approaches like Label Propagation (LP) or in Graph Neural Networks (GNN). Nonetheless, uncertainty estimation for non-independent node-level predictions is under-explored. In this work, we explore uncertainty quantification for node classification in three ways: (1) We derive three axioms explicitly characterizing the expected predictive uncertainty behavior in homophilic attributed graphs. (2) We propose a new model Graph Posterior Network (GPN) which explicitly performs Bayesian posterior updates for predictions on interdependent nodes. GPN provably obeys the proposed axioms. (3) We extensively evaluate GPN and a strong set of baselines on semi-supervised node classification including detection of anomalous features, and detection of left-out classes. GPN outperforms existing approaches for uncertainty estimation in the experiments.