Convex Analysis at Infinity: An Introduction to Astral Space

Not all convex functions on $\mathbb{R}^n$ have finite minimizers; some can only be minimized by a sequence as it heads to infinity. In this work, we aim to develop a theory for understanding such minimizers at infinity. We study astral space, a compact extension of $\mathbb{R}^n$ to which such points at infinity have been added. Astral space is constructed to be as small as possible while still ensuring that all linear functions can be continuously extended to the new space. Although astral space includes all of $\mathbb{R}^n$, it is not a vector space, nor even a metric space. However, it is sufficiently well-structured to allow useful and meaningful extensions of concepts of convexity, conjugacy, and subdifferentials. We develop these concepts and analyze various properties of convex functions on astral space, including the detailed structure of their minimizers, exact characterizations of continuity, and convergence of descent algorithms.

VScript: Controllable Script Generation with Audio-Visual Presentation

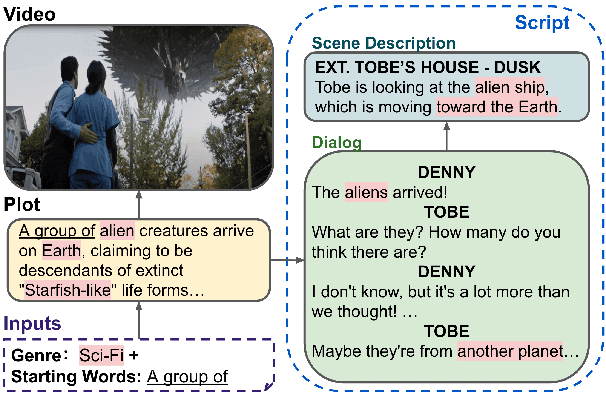
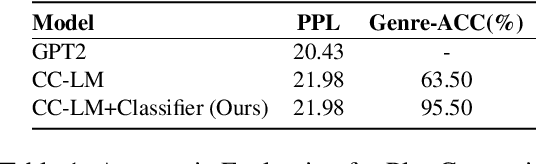
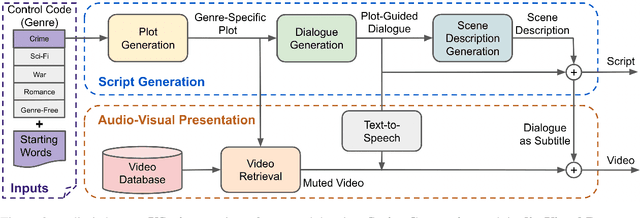
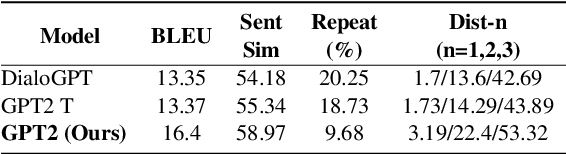
Automatic script generation could save a considerable amount of resources and offer inspiration to professional scriptwriters. We present VScript, a controllable pipeline that generates complete scripts including dialogues and scene descriptions, and presents visually using video retrieval and aurally using text-to-speech for spoken dialogue. With an interactive interface, our system allows users to select genres and input starting words that control the theme and development of the generated script. We adopt a hierarchical structure, which generates the plot, then the script and its audio-visual presentation. We also introduce a novel approach to plot-guided dialogue generation by treating it as an inverse dialogue summarization. Experiment results show that our approach outperforms the baselines on both automatic and human evaluations, especially in terms of genre control.

Reproducibility in Optimization: Theoretical Framework and Limits

We initiate a formal study of reproducibility in optimization. We define a quantitative measure of reproducibility of optimization procedures in the face of noisy or error-prone operations such as inexact or stochastic gradient computations or inexact initialization. We then analyze several convex optimization settings of interest such as smooth, non-smooth, and strongly-convex objective functions and establish tight bounds on the limits of reproducibility in each setting. Our analysis reveals a fundamental trade-off between computation and reproducibility: more computation is necessary (and sufficient) for better reproducibility.

Survey of Hallucination in Natural Language Generation

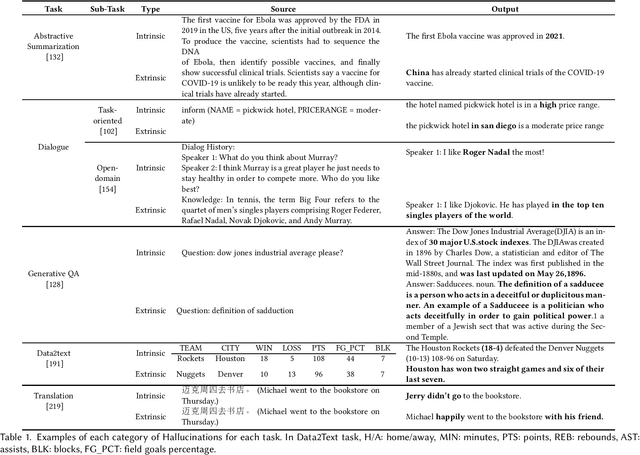
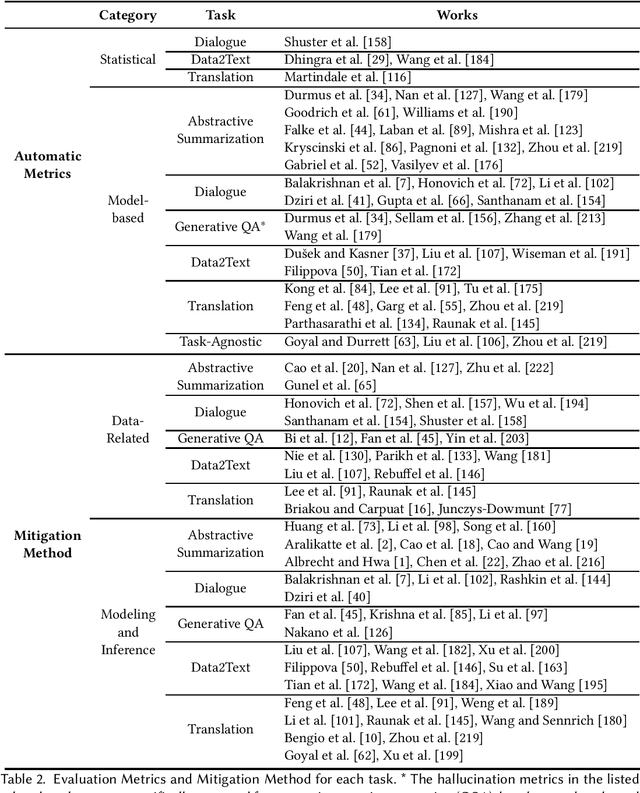
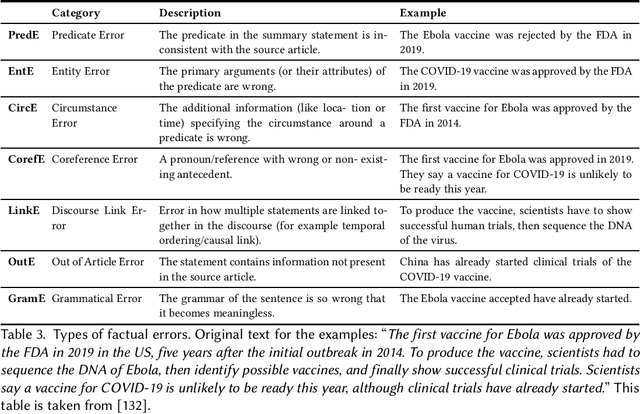
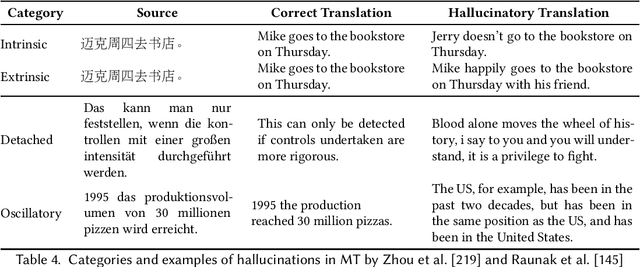
Natural Language Generation (NLG) has improved exponentially in recent years thanks to the development of deep learning technologies such as Transformer-based language models. This advancement has led to more fluent and coherent natural language generation, naturally leading to development in downstream tasks such as abstractive summarization, dialogue generation and data-to-text generation. However, it is also investigated that such generation includes hallucinated texts, which makes the performances of text generation fail to meet users' expectations in many real-world scenarios. In order to address this issue, studies in evaluation and mitigation methods of hallucinations have been presented in various tasks, but have not been reviewed in a combined manner. In this survey, we provide a broad overview of the research progress and challenges in the hallucination problem of NLG. The survey is organized into two big divisions: (i) a general overview of metrics, mitigation methods, and future directions; (ii) task-specific research progress for hallucinations in a large set of downstream tasks: abstractive summarization, dialogue generation, generative question answering, data-to-text generation, and machine translation. This survey could facilitate collaborative efforts among researchers in these tasks.

Agnostic Learnability of Halfspaces via Logistic Loss

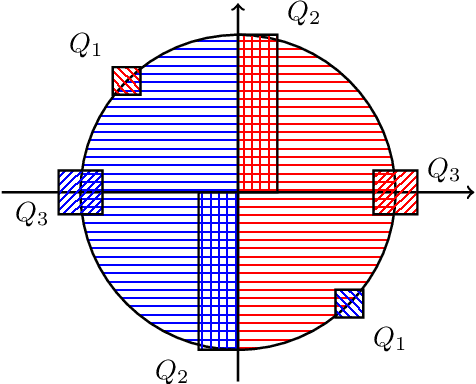
We investigate approximation guarantees provided by logistic regression for the fundamental problem of agnostic learning of homogeneous halfspaces. Previously, for a certain broad class of "well-behaved" distributions on the examples, Diakonikolas et al. (2020) proved an $\tilde{\Omega}(\textrm{OPT})$ lower bound, while Frei et al. (2021) proved an $\tilde{O}(\sqrt{\textrm{OPT}})$ upper bound, where $\textrm{OPT}$ denotes the best zero-one/misclassification risk of a homogeneous halfspace. In this paper, we close this gap by constructing a well-behaved distribution such that the global minimizer of the logistic risk over this distribution only achieves $\Omega(\sqrt{\textrm{OPT}})$ misclassification risk, matching the upper bound in (Frei et al., 2021). On the other hand, we also show that if we impose a radial-Lipschitzness condition in addition to well-behaved-ness on the distribution, logistic regression on a ball of bounded radius reaches $\tilde{O}(\textrm{OPT})$ misclassification risk. Our techniques also show for any well-behaved distribution, regardless of radial Lipschitzness, we can overcome the $\Omega(\sqrt{\textrm{OPT}})$ lower bound for logistic loss simply at the cost of one additional convex optimization step involving the hinge loss and attain $\tilde{O}(\textrm{OPT})$ misclassification risk. This two-step convex optimization algorithm is simpler than previous methods obtaining this guarantee, all of which require solving $O(\log(1/\textrm{OPT}))$ minimization problems.

Actor-critic is implicitly biased towards high entropy optimal policies

We show that the simplest actor-critic method -- a linear softmax policy updated with TD through interaction with a linear MDP, but featuring no explicit regularization or exploration -- does not merely find an optimal policy, but moreover prefers high entropy optimal policies. To demonstrate the strength of this bias, the algorithm not only has no regularization, no projections, and no exploration like $\epsilon$-greedy, but is moreover trained on a single trajectory with no resets. The key consequence of the high entropy bias is that uniform mixing assumptions on the MDP, which exist in some form in all prior work, can be dropped: the implicit regularization of the high entropy bias is enough to ensure that all chains mix and an optimal policy is reached with high probability. As auxiliary contributions, this work decouples concerns between the actor and critic by writing the actor update as an explicit mirror descent, provides tools to uniformly bound mixing times within KL balls of policy space, and provides a projection-free TD analysis with its own implicit bias which can be run from an unmixed starting distribution.

Fast Margin Maximization via Dual Acceleration

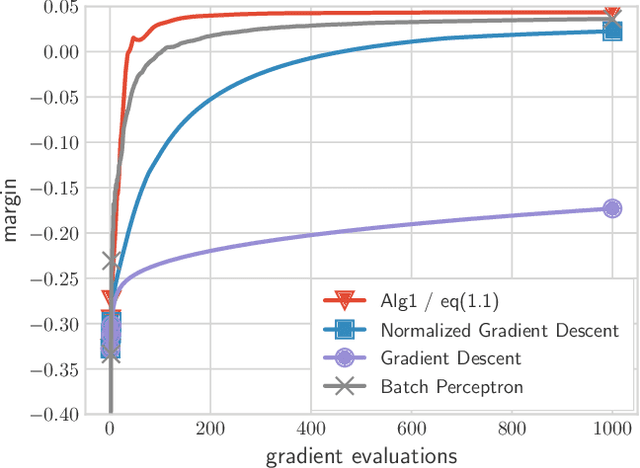
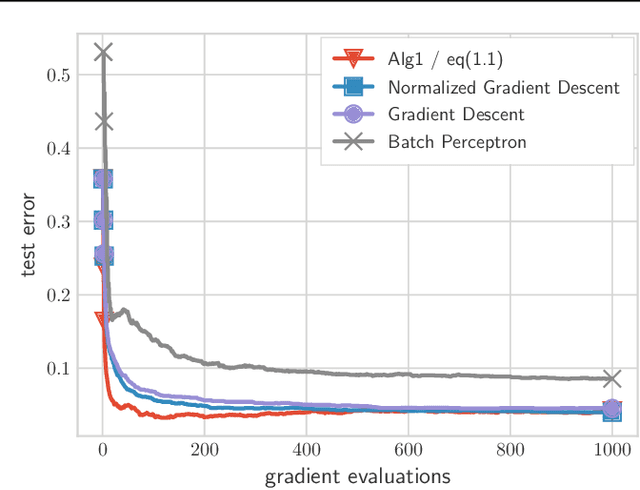
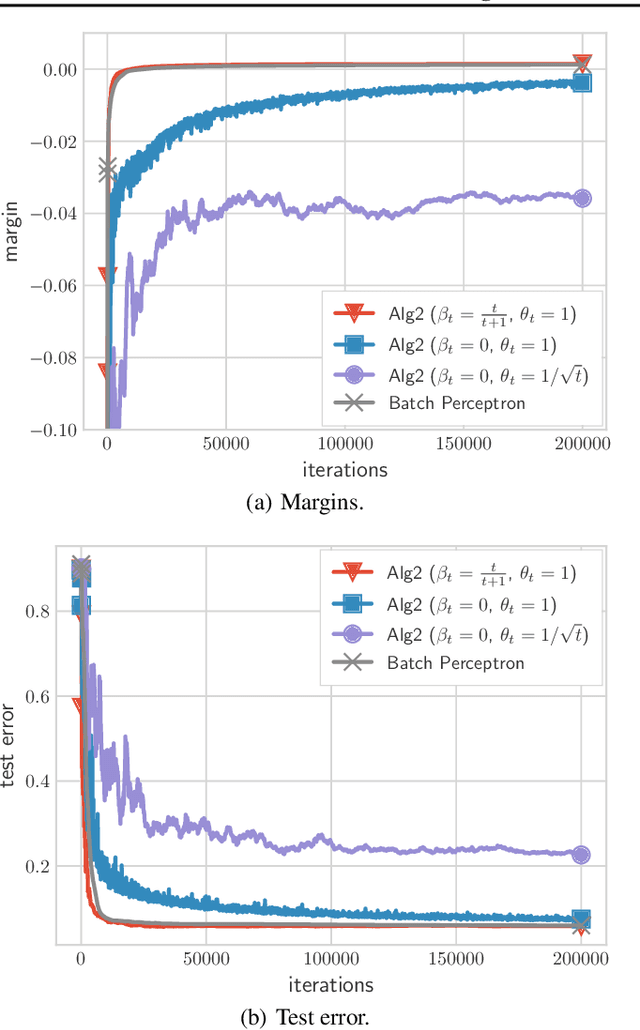
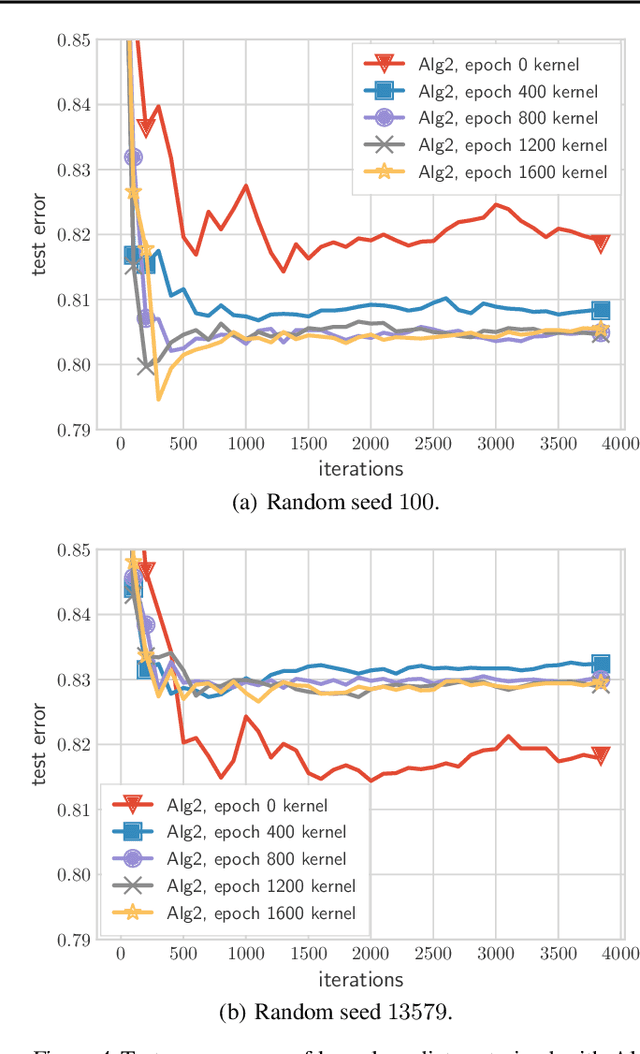
We present and analyze a momentum-based gradient method for training linear classifiers with an exponentially-tailed loss (e.g., the exponential or logistic loss), which maximizes the classification margin on separable data at a rate of $\widetilde{\mathcal{O}}(1/t^2)$. This contrasts with a rate of $\mathcal{O}(1/\log(t))$ for standard gradient descent, and $\mathcal{O}(1/t)$ for normalized gradient descent. This momentum-based method is derived via the convex dual of the maximum-margin problem, and specifically by applying Nesterov acceleration to this dual, which manages to result in a simple and intuitive method in the primal. This dual view can also be used to derive a stochastic variant, which performs adaptive non-uniform sampling via the dual variables.

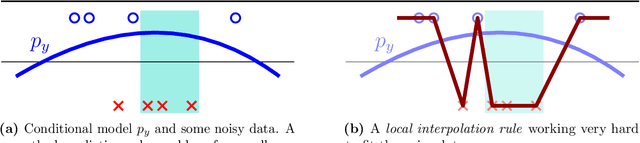
Early-stopped neural networks are consistent

This work studies the behavior of neural networks trained with the logistic loss via gradient descent on binary classification data where the underlying data distribution is general, and the (optimal) Bayes risk is not necessarily zero. In this setting, it is shown that gradient descent with early stopping achieves population risk arbitrarily close to optimal in terms of not just logistic and misclassification losses, but also in terms of calibration, meaning the sigmoid mapping of its outputs approximates the true underlying conditional distribution arbitrarily finely. Moreover, the necessary iteration, sample, and architectural complexities of this analysis all scale naturally with a certain complexity measure of the true conditional model. Lastly, while it is not shown that early stopping is necessary, it is shown that any univariate classifier satisfying a local interpolation property is necessarily inconsistent.

Generalization bounds via distillation

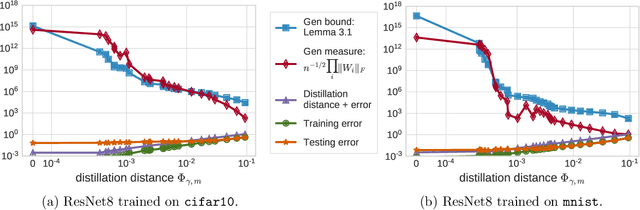
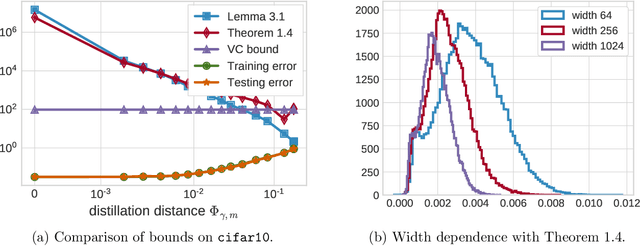
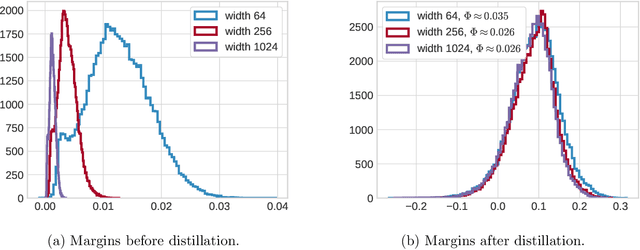
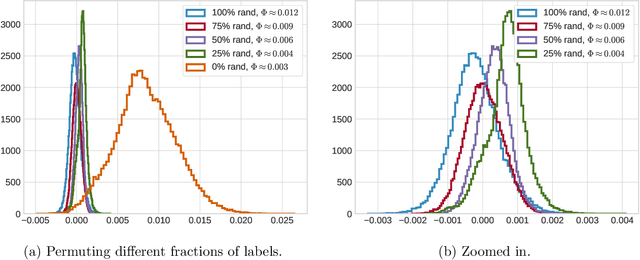
This paper theoretically investigates the following empirical phenomenon: given a high-complexity network with poor generalization bounds, one can distill it into a network with nearly identical predictions but low complexity and vastly smaller generalization bounds. The main contribution is an analysis showing that the original network inherits this good generalization bound from its distillation, assuming the use of well-behaved data augmentation. This bound is presented both in an abstract and in a concrete form, the latter complemented by a reduction technique to handle modern computation graphs featuring convolutional layers, fully-connected layers, and skip connections, to name a few. To round out the story, a (looser) classical uniform convergence analysis of compression is also presented, as well as a variety of experiments on cifar and mnist demonstrating similar generalization performance between the original network and its distillation.

Model Generalization on COVID-19 Fake News Detection

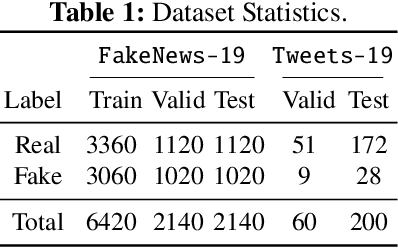
Amid the pandemic COVID-19, the world is facing unprecedented infodemic with the proliferation of both fake and real information. Considering the problematic consequences that the COVID-19 fake-news have brought, the scientific community has put effort to tackle it. To contribute to this fight against the infodemic, we aim to achieve a robust model for the COVID-19 fake-news detection task proposed at CONSTRAINT 2021 (FakeNews-19) by taking two separate approaches: 1) fine-tuning transformers based language models with robust loss functions and 2) removing harmful training instances through influence calculation. We further evaluate the robustness of our models by evaluating on different COVID-19 misinformation test set (Tweets-19) to understand model generalization ability. With the first approach, we achieve 98.13% for weighted F1 score (W-F1) for the shared task, whereas 38.18% W-F1 on the Tweets-19 highest. On the contrary, by performing influence data cleansing, our model with 99% cleansing percentage can achieve 54.33% W-F1 score on Tweets-19 with a trade-off. By evaluating our models on two COVID-19 fake-news test sets, we suggest the importance of model generalization ability in this task to step forward to tackle the COVID-19 fake-news problem in online social media platforms.