The WMDP Benchmark: Measuring and Reducing Malicious Use With Unlearning

The White House Executive Order on Artificial Intelligence highlights the risks of large language models (LLMs) empowering malicious actors in developing biological, cyber, and chemical weapons. To measure these risks of malicious use, government institutions and major AI labs are developing evaluations for hazardous capabilities in LLMs. However, current evaluations are private, preventing further research into mitigating risk. Furthermore, they focus on only a few, highly specific pathways for malicious use. To fill these gaps, we publicly release the Weapons of Mass Destruction Proxy (WMDP) benchmark, a dataset of 4,157 multiple-choice questions that serve as a proxy measurement of hazardous knowledge in biosecurity, cybersecurity, and chemical security. WMDP was developed by a consortium of academics and technical consultants, and was stringently filtered to eliminate sensitive information prior to public release. WMDP serves two roles: first, as an evaluation for hazardous knowledge in LLMs, and second, as a benchmark for unlearning methods to remove such hazardous knowledge. To guide progress on unlearning, we develop CUT, a state-of-the-art unlearning method based on controlling model representations. CUT reduces model performance on WMDP while maintaining general capabilities in areas such as biology and computer science, suggesting that unlearning may be a concrete path towards reducing malicious use from LLMs. We release our benchmark and code publicly at https://wmdp.ai

On Achieving Optimal Adversarial Test Error

We first elucidate various fundamental properties of optimal adversarial predictors: the structure of optimal adversarial convex predictors in terms of optimal adversarial zero-one predictors, bounds relating the adversarial convex loss to the adversarial zero-one loss, and the fact that continuous predictors can get arbitrarily close to the optimal adversarial error for both convex and zero-one losses. Applying these results along with new Rademacher complexity bounds for adversarial training near initialization, we prove that for general data distributions and perturbation sets, adversarial training on shallow networks with early stopping and an idealized optimal adversary is able to achieve optimal adversarial test error. By contrast, prior theoretical work either considered specialized data distributions or only provided training error guarantees.

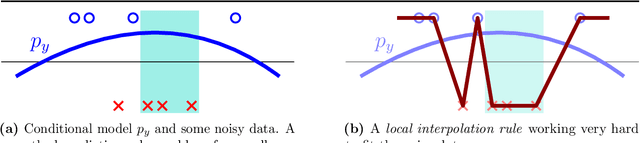
Early-stopped neural networks are consistent

This work studies the behavior of neural networks trained with the logistic loss via gradient descent on binary classification data where the underlying data distribution is general, and the (optimal) Bayes risk is not necessarily zero. In this setting, it is shown that gradient descent with early stopping achieves population risk arbitrarily close to optimal in terms of not just logistic and misclassification losses, but also in terms of calibration, meaning the sigmoid mapping of its outputs approximates the true underlying conditional distribution arbitrarily finely. Moreover, the necessary iteration, sample, and architectural complexities of this analysis all scale naturally with a certain complexity measure of the true conditional model. Lastly, while it is not shown that early stopping is necessary, it is shown that any univariate classifier satisfying a local interpolation property is necessarily inconsistent.