Apple Intelligence Foundation Language Models

We present foundation language models developed to power Apple Intelligence features, including a ~3 billion parameter model designed to run efficiently on devices and a large server-based language model designed for Private Cloud Compute. These models are designed to perform a wide range of tasks efficiently, accurately, and responsibly. This report describes the model architecture, the data used to train the model, the training process, how the models are optimized for inference, and the evaluation results. We highlight our focus on Responsible AI and how the principles are applied throughout the model development.

On Loop Formulas with Variables

Recently Ferraris, Lee and Lifschitz proposed a new definition of stable models that does not refer to grounding, which applies to the syntax of arbitrary first-order sentences. We show its relation to the idea of loop formulas with variables by Chen, Lin, Wang and Zhang, and generalize their loop formulas to disjunctive programs and to arbitrary first-order sentences. We also extend the syntax of logic programs to allow explicit quantifiers, and define its semantics as a subclass of the new language of stable models by Ferraris et al. Such programs inherit from the general language the ability to handle nonmonotonic reasoning under the stable model semantics even in the absence of the unique name and the domain closure assumptions, while yielding more succinct loop formulas than the general language due to the restricted syntax. We also show certain syntactic conditions under which query answering for an extended program can be reduced to entailment checking in first-order logic, providing a way to apply first-order theorem provers to reasoning about non-Herbrand stable models.

Are Interpretations Fairly Evaluated? A Definition Driven Pipeline for Post-Hoc Interpretability

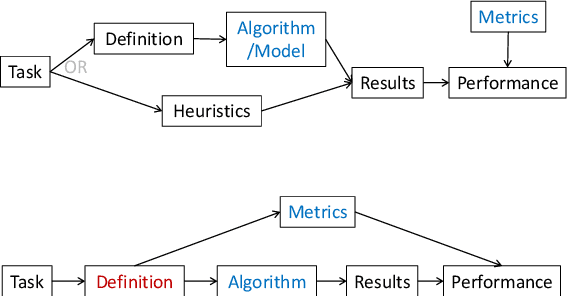
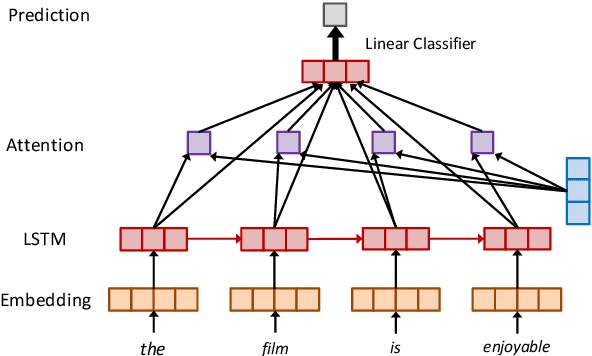
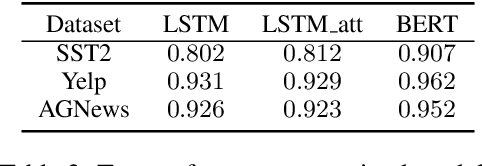
Recent years have witnessed an increasing number of interpretation methods being developed for improving transparency of NLP models. Meanwhile, researchers also try to answer the question that whether the obtained interpretation is faithful in explaining mechanisms behind model prediction? Specifically, (Jain and Wallace, 2019) proposes that "attention is not explanation" by comparing attention interpretation with gradient alternatives. However, it raises a new question that can we safely pick one interpretation method as the ground-truth? If not, on what basis can we compare different interpretation methods? In this work, we propose that it is crucial to have a concrete definition of interpretation before we could evaluate faithfulness of an interpretation. The definition will affect both the algorithm to obtain interpretation and, more importantly, the metric used in evaluation. Through both theoretical and experimental analysis, we find that although interpretation methods perform differently under a certain evaluation metric, such a difference may not result from interpretation quality or faithfulness, but rather the inherent bias of the evaluation metric.

Representing Hybrid Automata by Action Language Modulo Theories

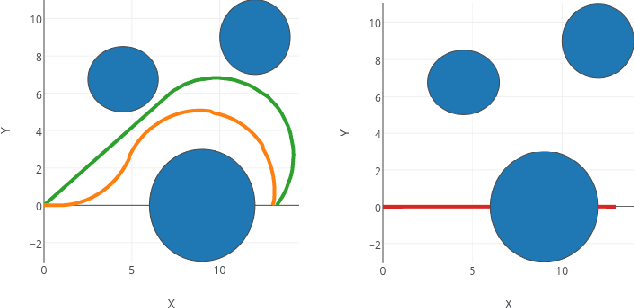
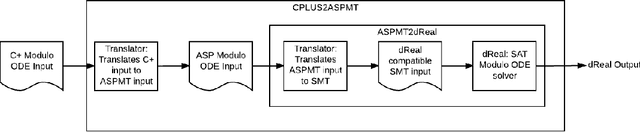
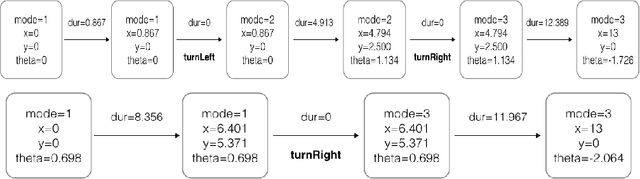
Both hybrid automata and action languages are formalisms for describing the evolution of dynamic systems. This paper establishes a formal relationship between them. We show how to succinctly represent hybrid automata in an action language which in turn is defined as a high-level notation for answer set programming modulo theories (ASPMT) --- an extension of answer set programs to the first-order level similar to the way satisfiability modulo theories (SMT) extends propositional satisfiability (SAT). We first show how to represent linear hybrid automata with convex invariants by an action language modulo theories. A further translation into SMT allows for computing them using SMT solvers that support arithmetic over reals. Next, we extend the representation to the general class of non-linear hybrid automata allowing even non-convex invariants. We represent them by an action language modulo ODE (Ordinary Differential Equations), which can be compiled into satisfiability modulo ODE. We developed a prototype system cplus2aspmt based on these translations, which allows for a succinct representation of hybrid transition systems that can be computed effectively by the state-of-the-art SMT solver dReal.

First-Order Stable Model Semantics and First-Order Loop Formulas

Lin and Zhaos theorem on loop formulas states that in the propositional case the stable model semantics of a logic program can be completely characterized by propositional loop formulas, but this result does not fully carry over to the first-order case. We investigate the precise relationship between the first-order stable model semantics and first-order loop formulas, and study conditions under which the former can be represented by the latter. In order to facilitate the comparison, we extend the definition of a first-order loop formula which was limited to a nondisjunctive program, to a disjunctive program and to an arbitrary first-order theory. Based on the studied relationship we extend the syntax of a logic program with explicit quantifiers, which allows us to do reasoning involving non-Herbrand stable models using first-order reasoners. Such programs can be viewed as a special class of first-order theories under the stable model semantics, which yields more succinct loop formulas than the general language due to their restricted syntax.

Two New Definitions of Stable Models of Logic Programs with Generalized Quantifiers

We present alternative definitions of the first-order stable model semantics and its extension to incorporate generalized quantifiers by referring to the familiar notion of a reduct instead of referring to the SM operator in the original definitions. Also, we extend the FLP stable model semantics to allow generalized quantifiers by referring to an operator that is similar to the $\sm$ operator. For a reasonable syntactic class of logic programs, we show that the two stable model semantics of generalized quantifiers are interchangeable.