RetinalGPT: A Retinal Clinical Preference Conversational Assistant Powered by Large Vision-Language Models

Recently, Multimodal Large Language Models (MLLMs) have gained significant attention for their remarkable ability to process and analyze non-textual data, such as images, videos, and audio. Notably, several adaptations of general-domain MLLMs to the medical field have been explored, including LLaVA-Med. However, these medical adaptations remain insufficiently advanced in understanding and interpreting retinal images. In contrast, medical experts emphasize the importance of quantitative analyses for disease detection and interpretation. This underscores a gap between general-domain and medical-domain MLLMs: while general-domain MLLMs excel in broad applications, they lack the specialized knowledge necessary for precise diagnostic and interpretative tasks in the medical field. To address these challenges, we introduce \textit{RetinalGPT}, a multimodal conversational assistant for clinically preferred quantitative analysis of retinal images. Specifically, we achieve this by compiling a large retinal image dataset, developing a novel data pipeline, and employing customized visual instruction tuning to enhance both retinal analysis and enrich medical knowledge. In particular, RetinalGPT outperforms MLLM in the generic domain by a large margin in the diagnosis of retinal diseases in 8 benchmark retinal datasets. Beyond disease diagnosis, RetinalGPT features quantitative analyses and lesion localization, representing a pioneering step in leveraging LLMs for an interpretable and end-to-end clinical research framework. The code is available at https://github.com/Retinal-Research/RetinalGPT

Enhancing Alzheimer's Diagnosis: Leveraging Anatomical Landmarks in Graph Convolutional Neural Networks on Tetrahedral Meshes

Alzheimer's disease (AD) is a major neurodegenerative condition that affects millions around the world. As one of the main biomarkers in the AD diagnosis procedure, brain amyloid positivity is typically identified by positron emission tomography (PET), which is costly and invasive. Brain structural magnetic resonance imaging (sMRI) may provide a safer and more convenient solution for the AD diagnosis. Recent advances in geometric deep learning have facilitated sMRI analysis and early diagnosis of AD. However, determining AD pathology, such as brain amyloid deposition, in preclinical stage remains challenging, as less significant morphological changes can be observed. As a result, few AD classification models are generalizable to the brain amyloid positivity classification task. Blood-based biomarkers (BBBMs), on the other hand, have recently achieved remarkable success in predicting brain amyloid positivity and identifying individuals with high risk of being brain amyloid positive. However, individuals in medium risk group still require gold standard tests such as Amyloid PET for further evaluation. Inspired by the recent success of transformer architectures, we propose a geometric deep learning model based on transformer that is both scalable and robust to variations in input volumetric mesh size. Our work introduced a novel tokenization scheme for tetrahedral meshes, incorporating anatomical landmarks generated by a pre-trained Gaussian process model. Our model achieved superior classification performance in AD classification task. In addition, we showed that the model was also generalizable to the brain amyloid positivity prediction with individuals in the medium risk class, where BM alone cannot achieve a clear classification. Our work may enrich geometric deep learning research and improve AD diagnosis accuracy without using expensive and invasive PET scans.

Plasma-CycleGAN: Plasma Biomarker-Guided MRI to PET Cross-modality Translation Using Conditional CycleGAN

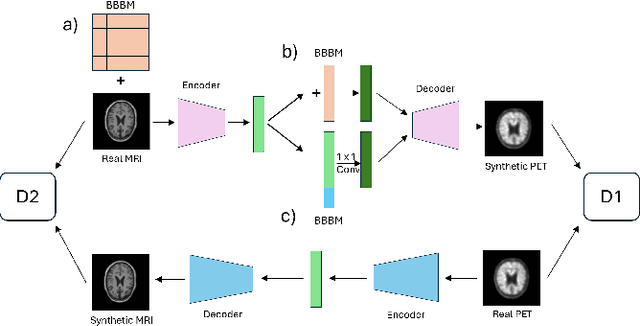
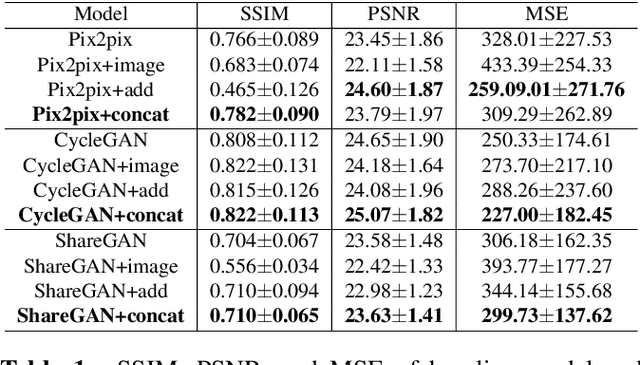
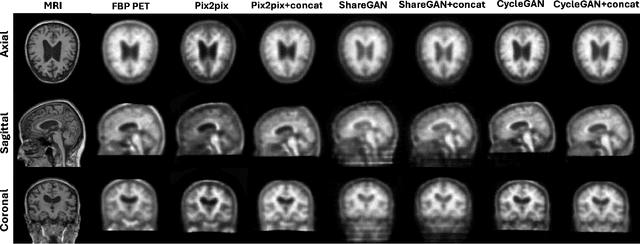
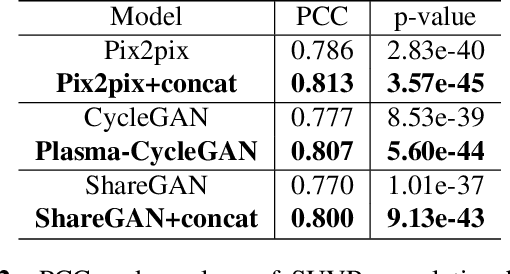
Cross-modality translation between MRI and PET imaging is challenging due to the distinct mechanisms underlying these modalities. Blood-based biomarkers (BBBMs) are revolutionizing Alzheimer's disease (AD) detection by identifying patients and quantifying brain amyloid levels. However, the potential of BBBMs to enhance PET image synthesis remains unexplored. In this paper, we performed a thorough study on the effect of incorporating BBBM into deep generative models. By evaluating three widely used cross-modality translation models, we found that BBBMs integration consistently enhances the generative quality across all models. By visual inspection of the generated results, we observed that PET images generated by CycleGAN exhibit the best visual fidelity. Based on these findings, we propose Plasma-CycleGAN, a novel generative model based on CycleGAN, to synthesize PET images from MRI using BBBMs as conditions. This is the first approach to integrate BBBMs in conditional cross-modality translation between MRI and PET.

Many-MobileNet: Multi-Model Augmentation for Robust Retinal Disease Classification

In this work, we propose Many-MobileNet, an efficient model fusion strategy for retinal disease classification using lightweight CNN architecture. Our method addresses key challenges such as overfitting and limited dataset variability by training multiple models with distinct data augmentation strategies and different model complexities. Through this fusion technique, we achieved robust generalization in data-scarce domains while balancing computational efficiency with feature extraction capabilities.

A Simple and Provable Scaling Law for the Test-Time Compute of Large Language Models

We propose a general two-stage algorithm that enjoys a provable scaling law for the test-time compute of large language models (LLMs). Given an input problem, the proposed algorithm first generates $N$ candidate solutions, and then chooses the best one via a multiple-round knockout tournament where each pair of candidates are compared for $K$ times and only the winners move on to the next round. In a minimalistic implementation, both stages can be executed with a black-box LLM alone and nothing else (e.g., no external verifier or reward model), and a total of $N \times (K + 1)$ highly parallelizable LLM calls are needed for solving an input problem. Assuming that a generated candidate solution is correct with probability $p_{\text{gen}} > 0$ and a comparison between a pair of correct and incorrect solutions identifies the right winner with probability $p_{\text{comp}} > 0.5$ (i.e., better than a random guess), we prove theoretically that the failure probability of the proposed algorithm decays to zero exponentially with respect to $N$ and $K$: $$\mathbb{P}(\text{final output is incorrect}) \le (1 - p_{\text{gen}})^N + \lceil \log_2 N \rceil e^{-2 K (p_{\text{comp}} - 0.5)^2}.$$ Our empirical results with the challenging MMLU-Pro benchmark validate the technical assumptions, as well as the efficacy of the proposed algorithm and the gains from scaling up its test-time compute.

CUNSB-RFIE: Context-aware Unpaired Neural Schrödinger Bridge in Retinal Fundus Image Enhancement

Retinal fundus photography is significant in diagnosing and monitoring retinal diseases. However, systemic imperfections and operator/patient-related factors can hinder the acquisition of high-quality retinal images. Previous efforts in retinal image enhancement primarily relied on GANs, which are limited by the trade-off between training stability and output diversity. In contrast, the Schr\"odinger Bridge (SB), offers a more stable solution by utilizing Optimal Transport (OT) theory to model a stochastic differential equation (SDE) between two arbitrary distributions. This allows SB to effectively transform low-quality retinal images into their high-quality counterparts. In this work, we leverage the SB framework to propose an image-to-image translation pipeline for retinal image enhancement. Additionally, previous methods often fail to capture fine structural details, such as blood vessels. To address this, we enhance our pipeline by introducing Dynamic Snake Convolution, whose tortuous receptive field can better preserve tubular structures. We name the resulting retinal fundus image enhancement framework the Context-aware Unpaired Neural Schr\"{o}dinger Bridge (CUNSB-RFIE). To the best of our knowledge, this is the first endeavor to use the SB approach for retinal image enhancement. Experimental results on a large-scale dataset demonstrate the advantage of the proposed method compared to several state-of-the-art supervised and unsupervised methods in terms of image quality and performance on downstream tasks.The code is available at https://github.com/Retinal-Research/CUNSB-RFIE .

AMG: Avatar Motion Guided Video Generation

Human video generation task has gained significant attention with the advancement of deep generative models. Generating realistic videos with human movements is challenging in nature, due to the intricacies of human body topology and sensitivity to visual artifacts. The extensively studied 2D media generation methods take advantage of massive human media datasets, but struggle with 3D-aware control; whereas 3D avatar-based approaches, while offering more freedom in control, lack photorealism and cannot be harmonized seamlessly with background scene. We propose AMG, a method that combines the 2D photorealism and 3D controllability by conditioning video diffusion models on controlled rendering of 3D avatars. We additionally introduce a novel data processing pipeline that reconstructs and renders human avatar movements from dynamic camera videos. AMG is the first method that enables multi-person diffusion video generation with precise control over camera positions, human motions, and background style. We also demonstrate through extensive evaluation that it outperforms existing human video generation methods conditioned on pose sequences or driving videos in terms of realism and adaptability.

On the Design and Analysis of LLM-Based Algorithms

We initiate a formal investigation into the design and analysis of LLM-based algorithms, i.e. algorithms that contain one or multiple calls of large language models (LLMs) as sub-routines and critically rely on the capabilities of LLMs. While LLM-based algorithms, ranging from basic LLM calls with prompt engineering to complicated LLM-powered agent systems and compound AI systems, have achieved remarkable empirical success, the design and optimization of them have mostly relied on heuristics and trial-and-errors, which is largely due to a lack of formal and analytical study for these algorithms. To fill this gap, we start by identifying the computational-graph representation of LLM-based algorithms, the design principle of task decomposition, and some key abstractions, which then facilitate our formal analysis for the accuracy and efficiency of LLM-based algorithms, despite the black-box nature of LLMs. We further consider parallel decomposition for a case study, providing extensive analytical and empirical study for four concrete examples of this pattern. Our proposed framework holds promise for advancing LLM-based algorithms, by revealing the reasons behind curious empirical phenomena, guiding the choices of hyperparameters, predicting the empirical performance of algorithms, and inspiring new algorithm design. To promote further study of LLM-based algorithms, we release our source code at https://github.com/modelscope/agentscope/tree/main/examples/paper_llm_based_algorithm.

Clustering Mixtures of Discrete Distributions: A Note on Mitra's Algorithm

In this note, we provide a refined analysis of Mitra's algorithm \cite{mitra2008clustering} for classifying general discrete mixture distribution models. Built upon spectral clustering \cite{mcsherry2001spectral}, this algorithm offers compelling conditions for probability distributions. We enhance this analysis by tailoring the model to bipartite stochastic block models, resulting in more refined conditions. Compared to those derived in \cite{mitra2008clustering}, our improved separation conditions are obtained.

Boosting Single Positive Multi-label Classification with Generalized Robust Loss

Multi-label learning (MLL) requires comprehensive multi-semantic annotations that is hard to fully obtain, thus often resulting in missing labels scenarios. In this paper, we investigate Single Positive Multi-label Learning (SPML), where each image is associated with merely one positive label. Existing SPML methods only focus on designing losses using mechanisms such as hard pseudo-labeling and robust losses, mostly leading to unacceptable false negatives. To address this issue, we first propose a generalized loss framework based on expected risk minimization to provide soft pseudo labels, and point out that the former losses can be seamlessly converted into our framework. In particular, we design a novel robust loss based on our framework, which enjoys flexible coordination between false positives and false negatives, and can additionally deal with the imbalance between positive and negative samples. Extensive experiments show that our approach can significantly improve SPML performance and outperform the vast majority of state-of-the-art methods on all the four benchmarks.