Search Arena: Analyzing Search-Augmented LLMs

Search-augmented language models combine web search with Large Language Models (LLMs) to improve response groundedness and freshness. However, analyzing these systems remains challenging: existing datasets are limited in scale and narrow in scope, often constrained to static, single-turn, fact-checking questions. In this work, we introduce Search Arena, a crowd-sourced, large-scale, human-preference dataset of over 24,000 paired multi-turn user interactions with search-augmented LLMs. The dataset spans diverse intents and languages, and contains full system traces with around 12,000 human preference votes. Our analysis reveals that user preferences are influenced by the number of citations, even when the cited content does not directly support the attributed claims, uncovering a gap between perceived and actual credibility. Furthermore, user preferences vary across cited sources, revealing that community-driven platforms are generally preferred and static encyclopedic sources are not always appropriate and reliable. To assess performance across different settings, we conduct cross-arena analyses by testing search-augmented LLMs in a general-purpose chat environment and conventional LLMs in search-intensive settings. We find that web search does not degrade and may even improve performance in non-search settings; however, the quality in search settings is significantly affected if solely relying on the model's parametric knowledge. We open-sourced the dataset to support future research in this direction. Our dataset and code are available at: https://github.com/lmarena/search-arena.

Understanding In-context Learning of Addition via Activation Subspaces

To perform in-context learning, language models must extract signals from individual few-shot examples, aggregate these into a learned prediction rule, and then apply this rule to new examples. How is this implemented in the forward pass of modern transformer models? To study this, we consider a structured family of few-shot learning tasks for which the true prediction rule is to add an integer $k$ to the input. We find that Llama-3-8B attains high accuracy on this task for a range of $k$, and localize its few-shot ability to just three attention heads via a novel optimization approach. We further show the extracted signals lie in a six-dimensional subspace, where four of the dimensions track the unit digit and the other two dimensions track overall magnitude. We finally examine how these heads extract information from individual few-shot examples, identifying a self-correction mechanism in which mistakes from earlier examples are suppressed by later examples. Our results demonstrate how tracking low-dimensional subspaces across a forward pass can provide insight into fine-grained computational structures.

Incentivizing High-Quality Content in Online Recommender Systems

For content recommender systems such as TikTok and YouTube, the platform's decision algorithm shapes the incentives of content producers, including how much effort the content producers invest in the quality of their content. Many platforms employ online learning, which creates intertemporal incentives, since content produced today affects recommendations of future content. In this paper, we study the incentives arising from online learning, analyzing the quality of content produced at a Nash equilibrium. We show that classical online learning algorithms, such as Hedge and EXP3, unfortunately incentivize producers to create low-quality content. In particular, the quality of content is upper bounded in terms of the learning rate and approaches zero for typical learning rate schedules. Motivated by this negative result, we design a different learning algorithm -- based on punishing producers who create low-quality content -- that correctly incentivizes producers to create high-quality content. At a conceptual level, our work illustrates the unintended impact that a platform's learning algorithm can have on content quality and opens the door towards designing platform learning algorithms that incentivize the creation of high-quality content.

Incentivizing Combinatorial Bandit Exploration

Consider a bandit algorithm that recommends actions to self-interested users in a recommendation system. The users are free to choose other actions and need to be incentivized to follow the algorithm's recommendations. While the users prefer to exploit, the algorithm can incentivize them to explore by leveraging the information collected from the previous users. All published work on this problem, known as incentivized exploration, focuses on small, unstructured action sets and mainly targets the case when the users' beliefs are independent across actions. However, realistic exploration problems often feature large, structured action sets and highly correlated beliefs. We focus on a paradigmatic exploration problem with structure: combinatorial semi-bandits. We prove that Thompson Sampling, when applied to combinatorial semi-bandits, is incentive-compatible when initialized with a sufficient number of samples of each arm (where this number is determined in advance by the Bayesian prior). Moreover, we design incentive-compatible algorithms for collecting the initial samples.

Nash Convergence of Mean-Based Learning Algorithms in First Price Auctions

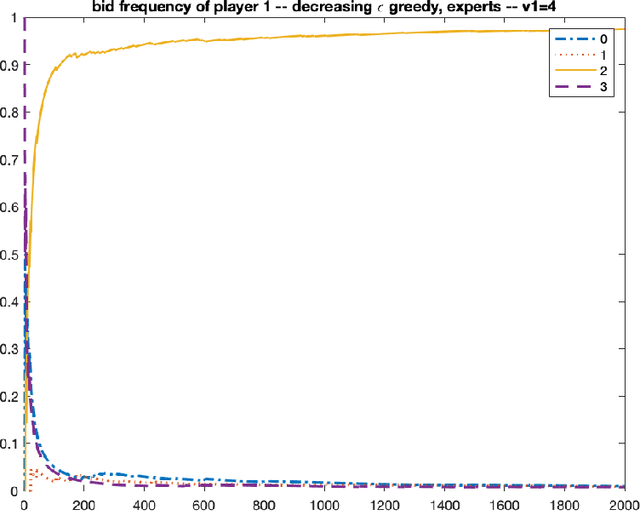
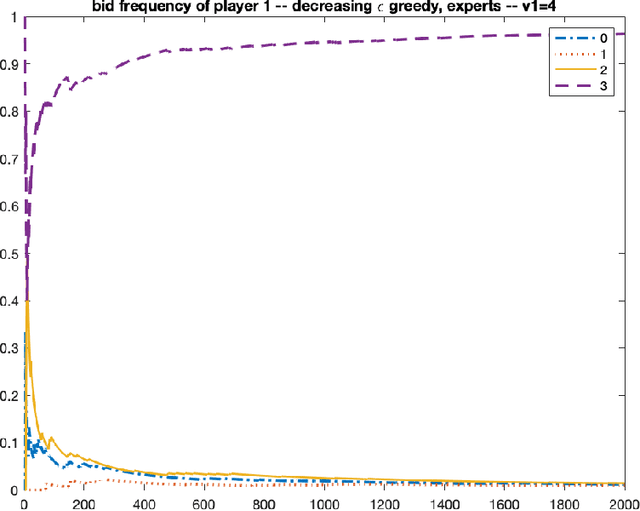
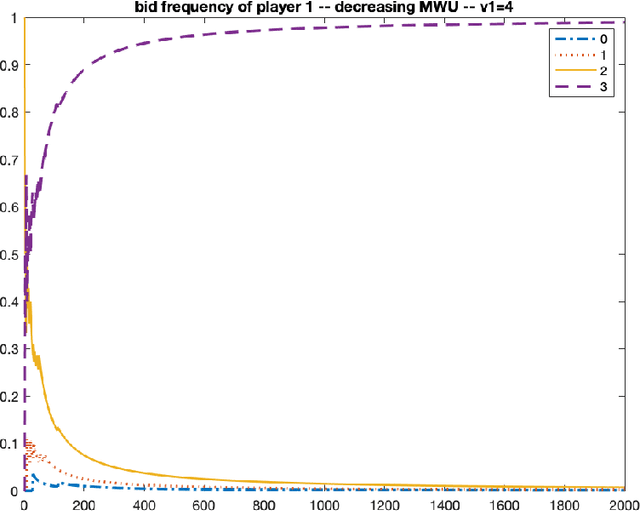
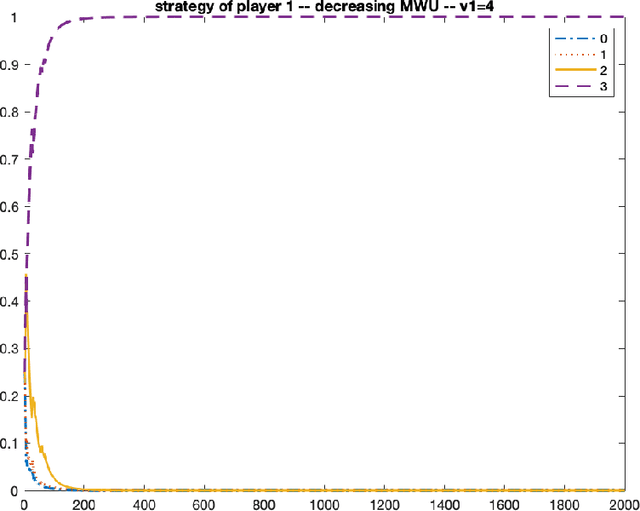
We consider repeated first price auctions where each bidder, having a deterministic type, learns to bid using a mean-based learning algorithm. We completely characterize the Nash convergence property of the bidding dynamics in two senses: (1) time-average: the fraction of rounds where bidders play a Nash equilibrium approaches to 1 in the limit; (2) last-iterate: the mixed strategy profile of bidders approaches to a Nash equilibrium in the limit. Specifically, the results depend on the number of bidders with the highest value: - If the number is at least three, the bidding dynamics almost surely converges to a Nash equilibrium of the auction, both in time-average and in last-iterate. - If the number is two, the bidding dynamics almost surely converges to a Nash equilibrium in time-average but not necessarily in last-iterate. - If the number is one, the bidding dynamics may not converge to a Nash equilibrium in time-average nor in last-iterate. Our discovery opens up new possibilities in the study of convergence dynamics of learning algorithms.