Interpreting Contact Interactions to Overcome Failure in Robot Assembly Tasks

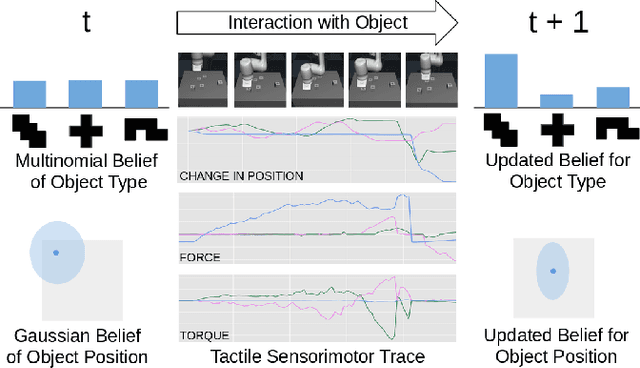
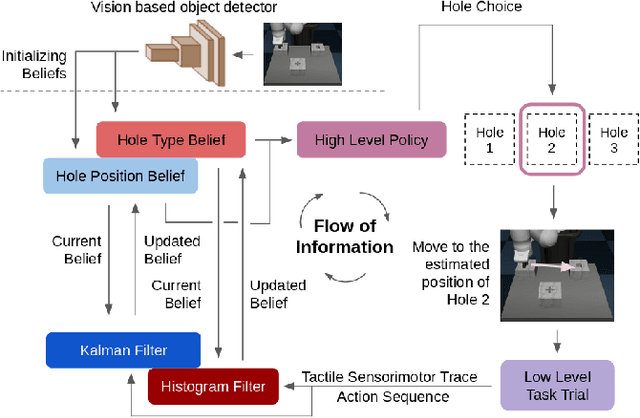
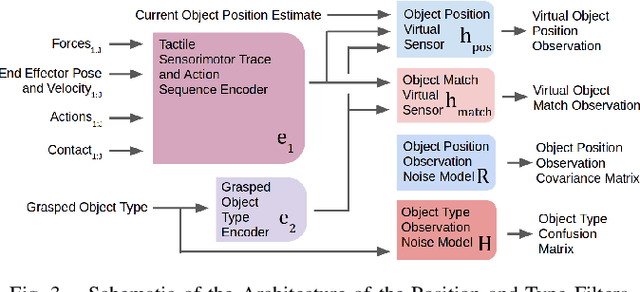
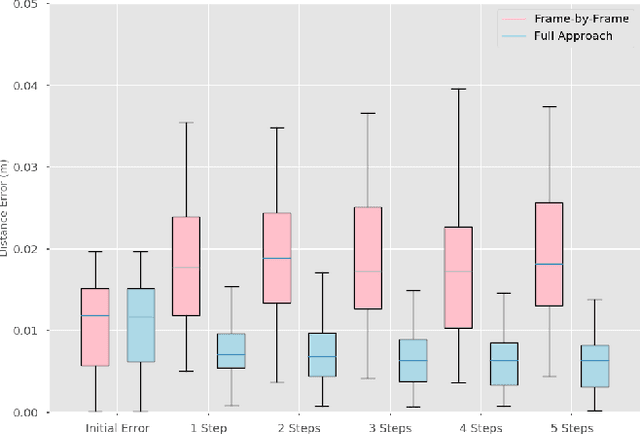
A key challenge towards the goal of multi-part assembly tasks is finding robust sensorimotor control methods in the presence of uncertainty. In contrast to previous works that rely on a priori knowledge on whether two parts match, we aim to learn this through physical interaction. We propose a hierachical approach that enables a robot to autonomously assemble parts while being uncertain about part types and positions. In particular, our probabilistic approach learns a set of differentiable filters that leverage the tactile sensorimotor trace from failed assembly attempts to update its belief about part position and type. This enables a robot to overcome assembly failure. We demonstrate the effectiveness of our approach on a set of object fitting tasks. The experimental results indicate that our proposed approach achieves higher precision in object position and type estimation, and accomplishes object fitting tasks faster than baselines.

Learning Dense Rewards for Contact-Rich Manipulation Tasks

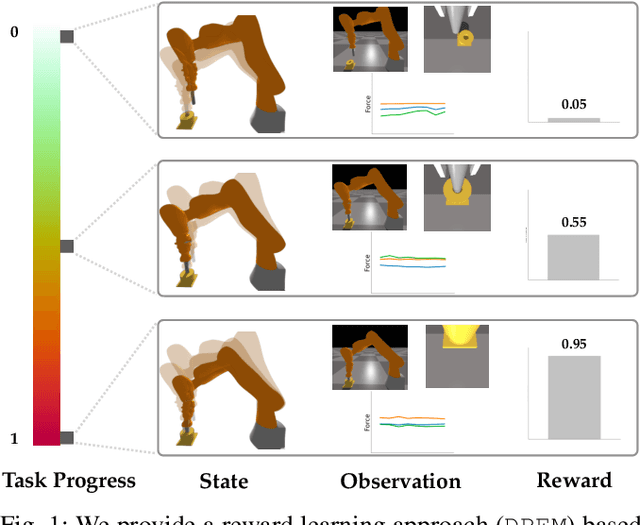
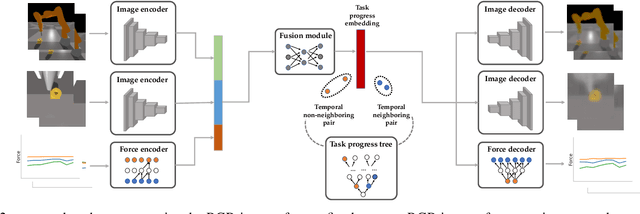
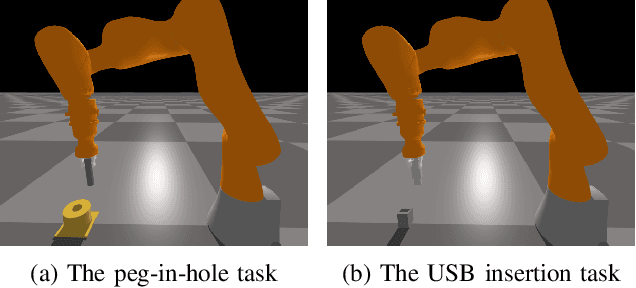
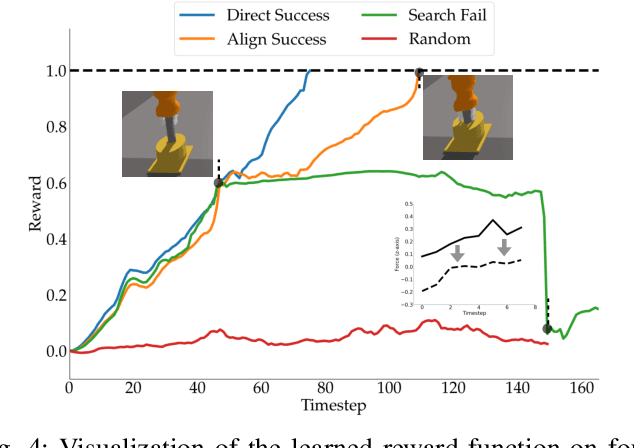
Rewards play a crucial role in reinforcement learning. To arrive at the desired policy, the design of a suitable reward function often requires significant domain expertise as well as trial-and-error. Here, we aim to minimize the effort involved in designing reward functions for contact-rich manipulation tasks. In particular, we provide an approach capable of extracting dense reward functions algorithmically from robots' high-dimensional observations, such as images and tactile feedback. In contrast to state-of-the-art high-dimensional reward learning methodologies, our approach does not leverage adversarial training, and is thus less prone to the associated training instabilities. Instead, our approach learns rewards by estimating task progress in a self-supervised manner. We demonstrate the effectiveness and efficiency of our approach on two contact-rich manipulation tasks, namely, peg-in-hole and USB insertion. The experimental results indicate that the policies trained with the learned reward function achieves better performance and faster convergence compared to the baselines.

Convex Factorization Machine for Regression

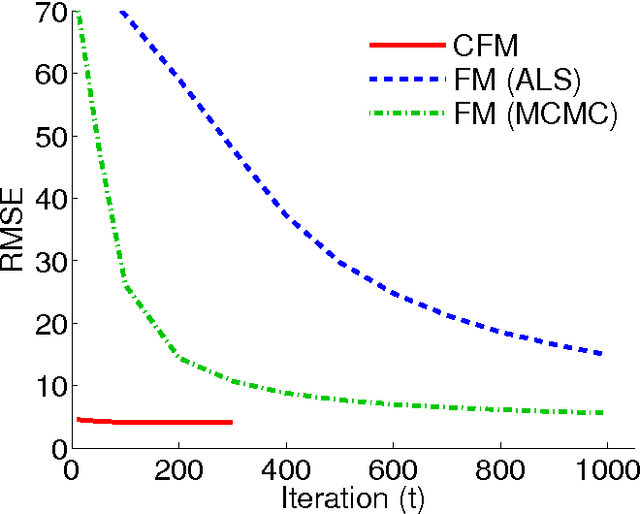
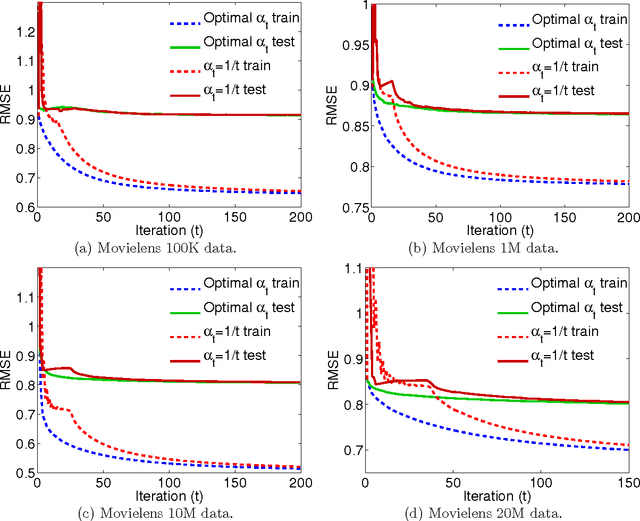
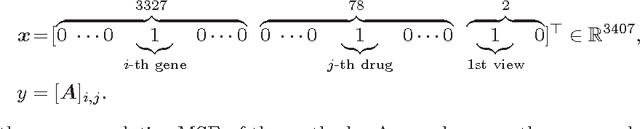
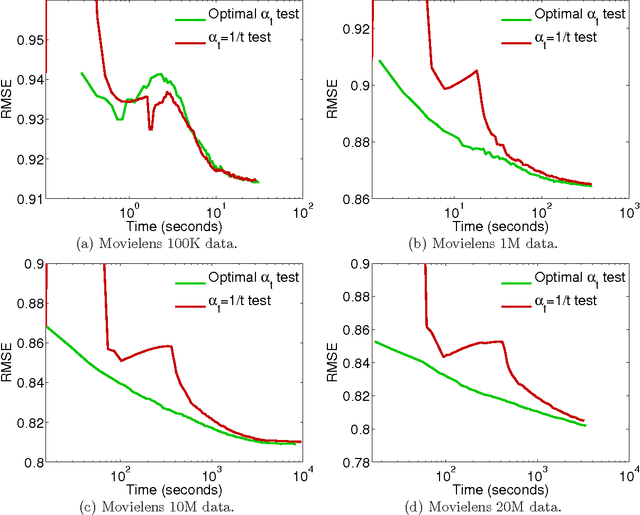
We propose the convex factorization machine (CFM), which is a convex variant of the widely used Factorization Machines (FMs). Specifically, we employ a linear+quadratic model and regularize the linear term with the $\ell_2$-regularizer and the quadratic term with the trace norm regularizer. Then, we formulate the CFM optimization as a semidefinite programming problem and propose an efficient optimization procedure with Hazan's algorithm. A key advantage of CFM over existing FMs is that it can find a globally optimal solution, while FMs may get a poor locally optimal solution since the objective function of FMs is non-convex. In addition, the proposed algorithm is simple yet effective and can be implemented easily. Finally, CFM is a general factorization method and can also be used for other factorization problems including including multi-view matrix factorization and tensor completion problems. Through synthetic and movielens datasets, we first show that the proposed CFM achieves results competitive to FMs. Furthermore, in a toxicogenomics prediction task, we show that CFM outperforms a state-of-the-art tensor factorization method.