Wasserstein Gradient Flow over Variational Parameter Space for Variational Inference

Variational inference (VI) can be cast as an optimization problem in which the variational parameters are tuned to closely align a variational distribution with the true posterior. The optimization task can be approached through vanilla gradient descent in black-box VI or natural-gradient descent in natural-gradient VI. In this work, we reframe VI as the optimization of an objective that concerns probability distributions defined over a \textit{variational parameter space}. Subsequently, we propose Wasserstein gradient descent for tackling this optimization problem. Notably, the optimization techniques, namely black-box VI and natural-gradient VI, can be reinterpreted as specific instances of the proposed Wasserstein gradient descent. To enhance the efficiency of optimization, we develop practical methods for numerically solving the discrete gradient flows. We validate the effectiveness of the proposed methods through empirical experiments on a synthetic dataset, supplemented by theoretical analyses.

CentSmoothie: Central-Smoothing Hypergraph Neural Networks for Predicting Drug-Drug Interactions

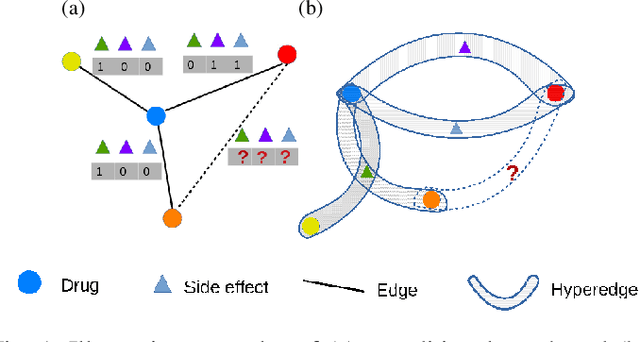
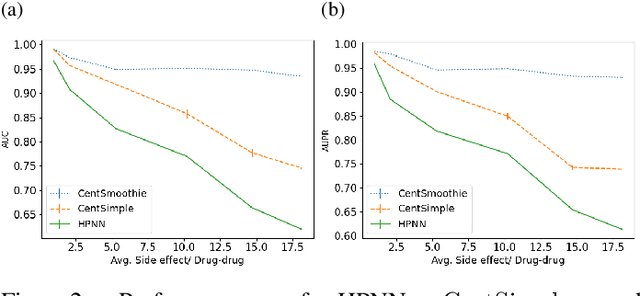
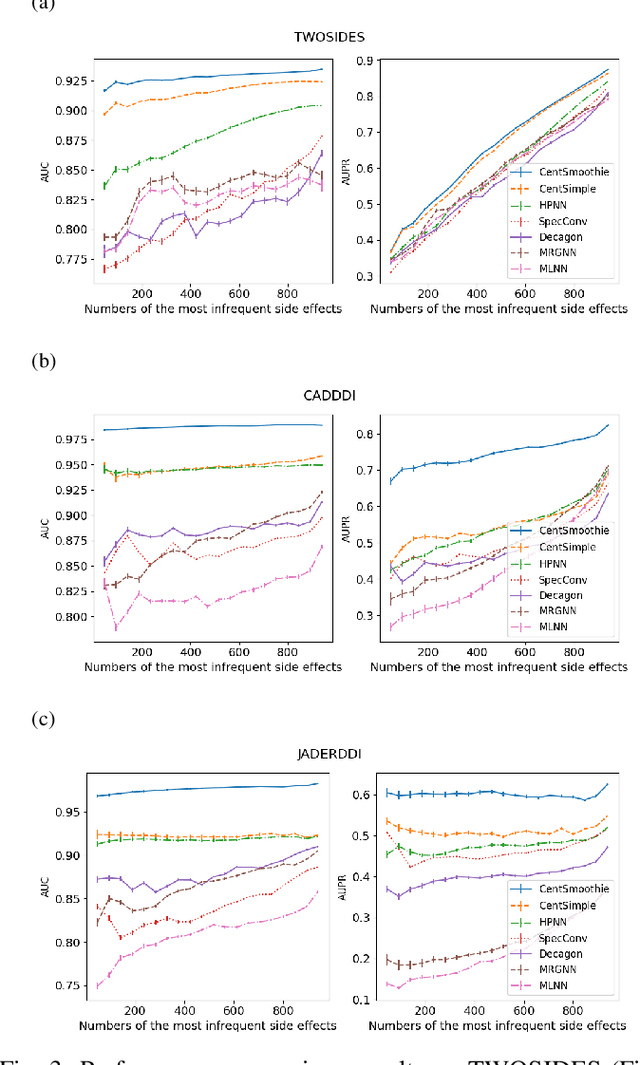
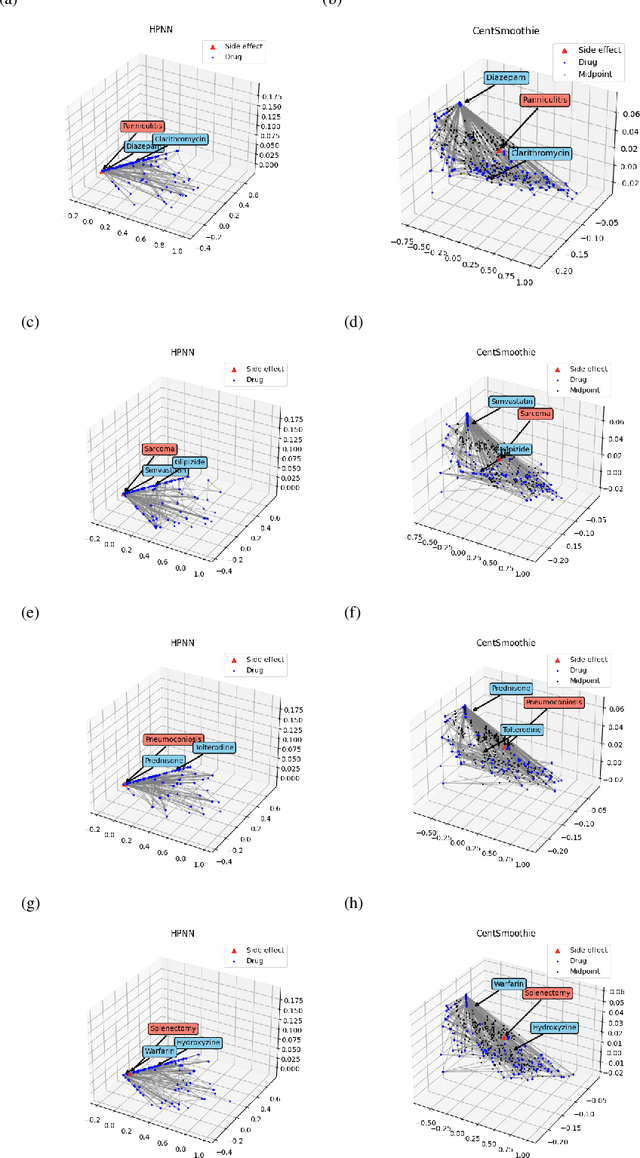
Predicting drug-drug interactions (DDI) is the problem of predicting side effects (unwanted outcomes) of a pair of drugs using drug information and known side effects of many pairs. This problem can be formulated as predicting labels (i.e. side effects) for each pair of nodes in a DDI graph, of which nodes are drugs and edges are interacting drugs with known labels. State-of-the-art methods for this problem are graph neural networks (GNNs), which leverage neighborhood information in the graph to learn node representations. For DDI, however, there are many labels with complicated relationships due to the nature of side effects. Usual GNNs often fix labels as one-hot vectors that do not reflect label relationships and potentially do not obtain the highest performance in the difficult cases of infrequent labels. In this paper, we formulate DDI as a hypergraph where each hyperedge is a triple: two nodes for drugs and one node for a label. We then present CentSmoothie, a hypergraph neural network that learns representations of nodes and labels altogether with a novel central-smoothing formulation. We empirically demonstrate the performance advantages of CentSmoothie in simulations as well as real datasets.

Learning subtree pattern importance for Weisfeiler-Lehmanbased graph kernels

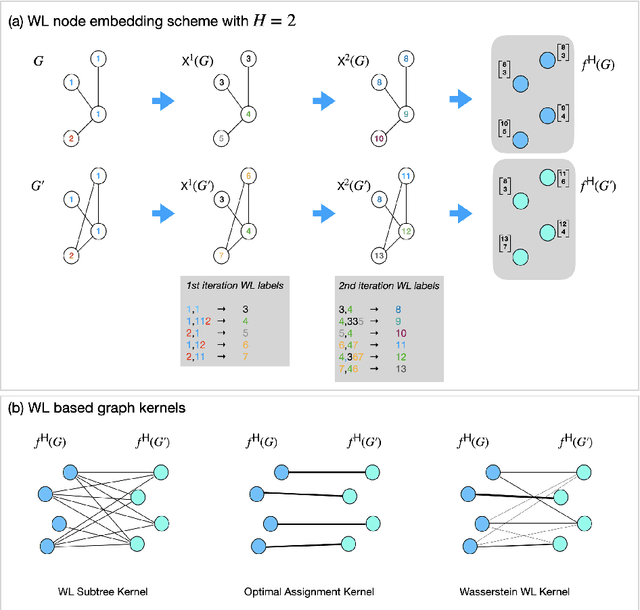
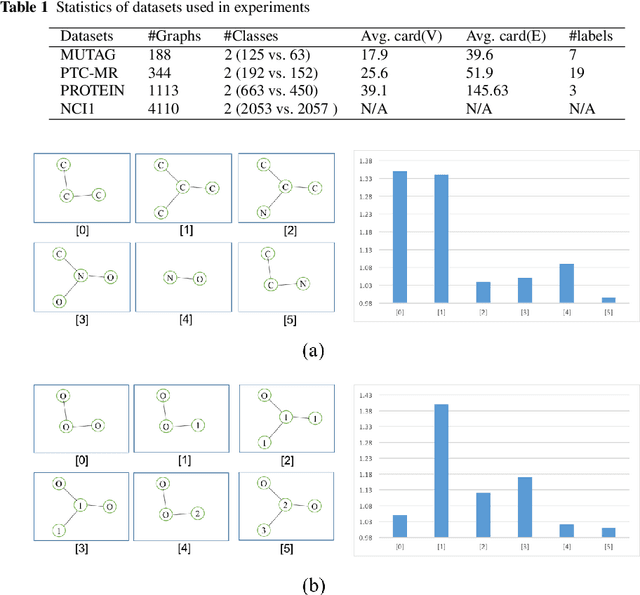
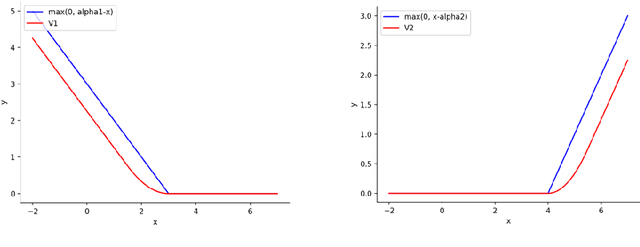
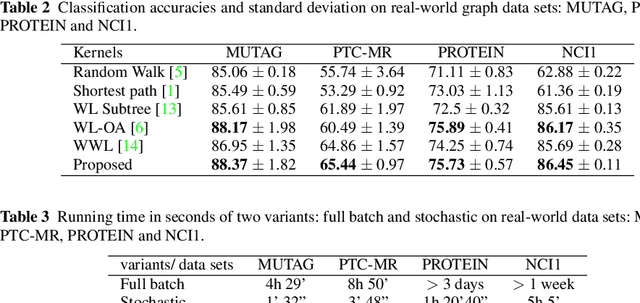
Graph is an usual representation of relational data, which are ubiquitous in manydomains such as molecules, biological and social networks. A popular approach to learningwith graph structured data is to make use of graph kernels, which measure the similaritybetween graphs and are plugged into a kernel machine such as a support vector machine.Weisfeiler-Lehman (WL) based graph kernels, which employ WL labeling scheme to extract subtree patterns and perform node embedding, are demonstrated to achieve great performance while being efficiently computable. However, one of the main drawbacks of ageneral kernel is the decoupling of kernel construction and learning process. For moleculargraphs, usual kernels such as WL subtree, based on substructures of the molecules, consider all available substructures having the same importance, which might not be suitable inpractice. In this paper, we propose a method to learn the weights of subtree patterns in the framework of WWL kernels, the state of the art method for graph classification task [14]. To overcome the computational issue on large scale data sets, we present an efficient learning algorithm and also derive a generalization gap bound to show its convergence. Finally, through experiments on synthetic and real-world data sets, we demonstrate the effectiveness of our proposed method for learning the weights of subtree patterns.

On Convex Clustering Solutions

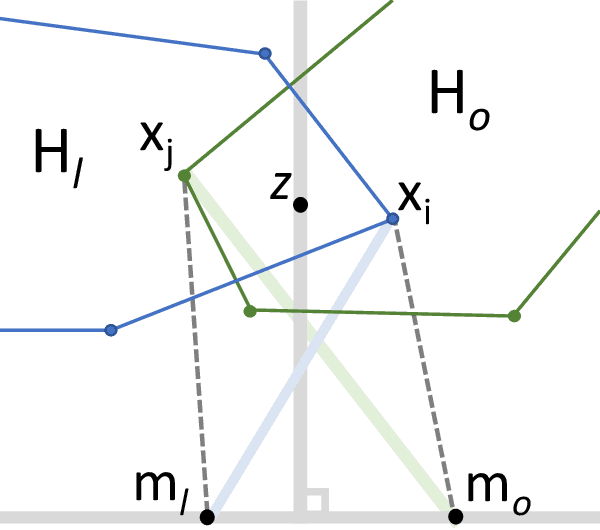
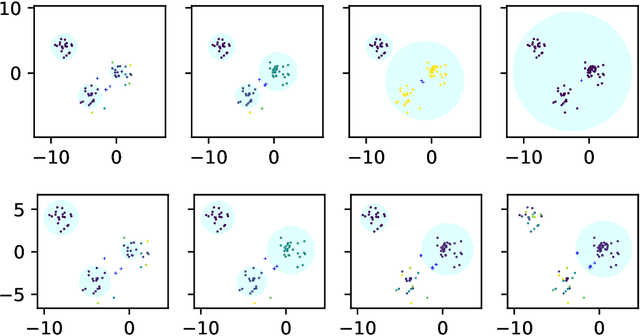
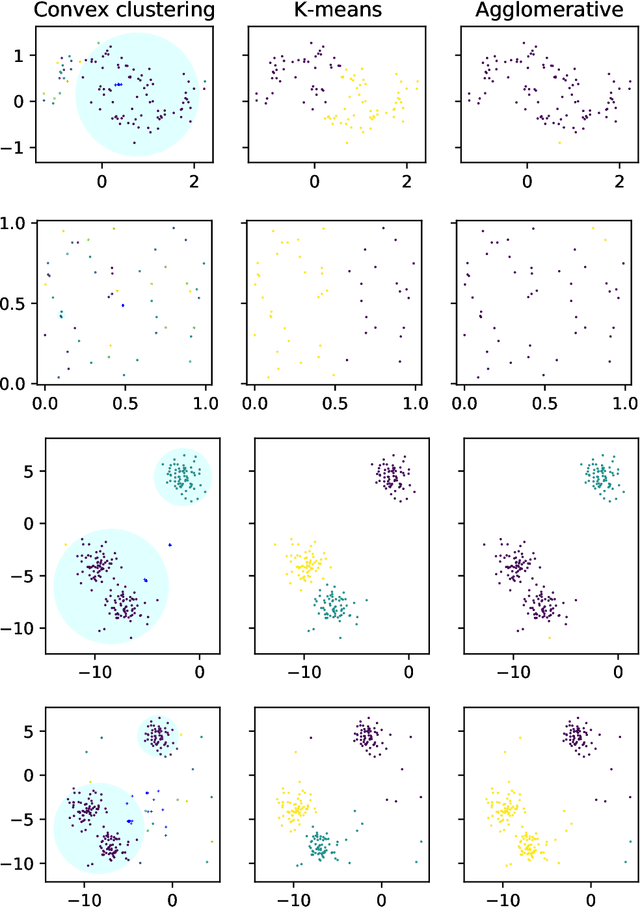
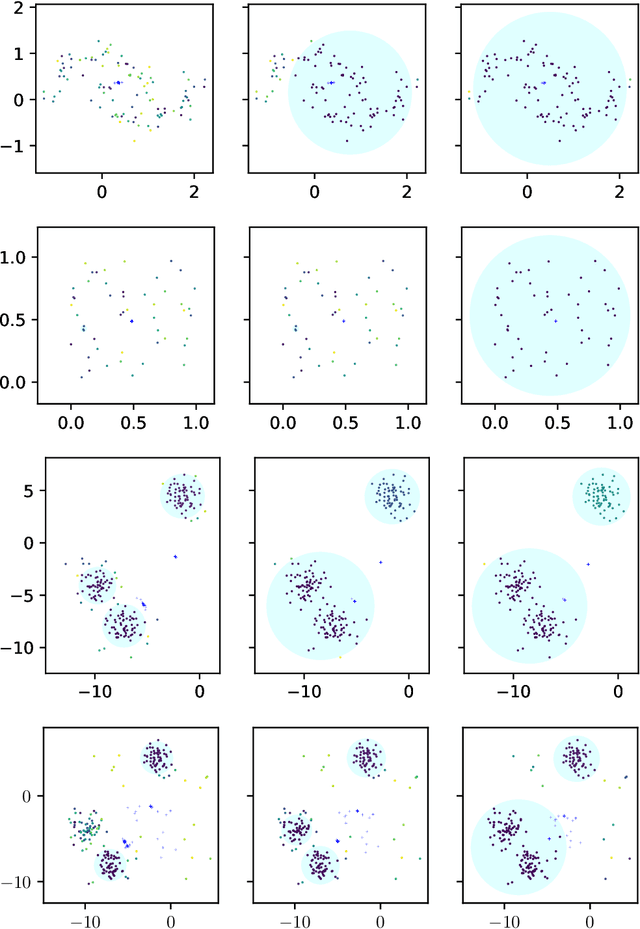
Convex clustering is an attractive clustering algorithm with favorable properties such as efficiency and optimality owing to its convex formulation. It is thought to generalize both k-means clustering and agglomerative clustering. However, it is not known whether convex clustering preserves desirable properties of these algorithms. A common expectation is that convex clustering may learn difficult cluster types such as non-convex ones. Current understanding of convex clustering is limited to only consistency results on well-separated clusters. We show new understanding of its solutions. We prove that convex clustering can only learn convex clusters. We then show that the clusters have disjoint bounding balls with significant gaps. We further characterize the solutions, regularization hyperparameters, inclusterable cases and consistency.

DIVERSE: bayesian Data IntegratiVE learning for precise drug ResponSE prediction

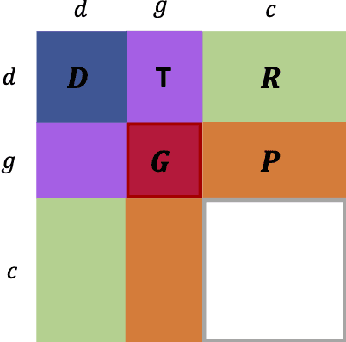
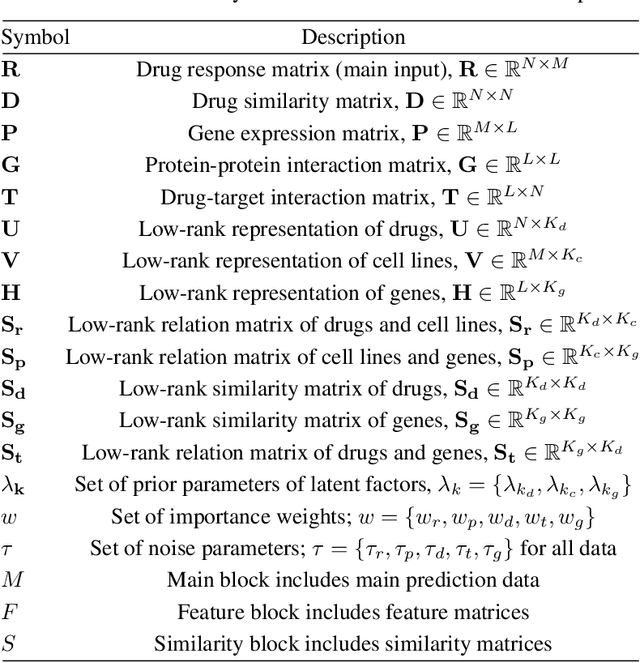
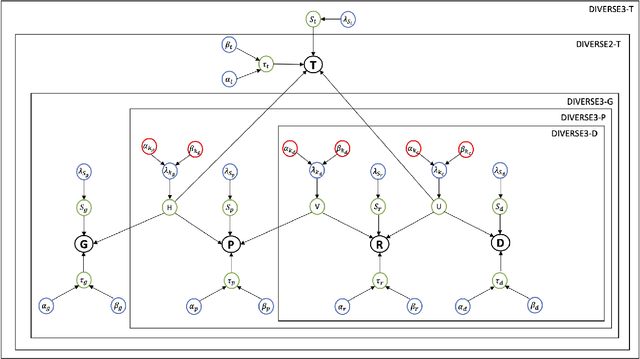
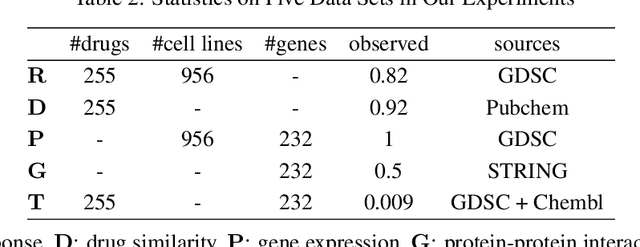
Detecting predictive biomarkers from multi-omics data is important for precision medicine, to improve diagnostics of complex diseases and for better treatments. This needs substantial experimental efforts that are made difficult by the heterogeneity of cell lines and huge cost. An effective solution is to build a computational model over the diverse omics data, including genomic, molecular, and environmental information. However, choosing informative and reliable data sources from among the different types of data is a challenging problem. We propose DIVERSE, a framework of Bayesian importance-weighted tri- and bi-matrix factorization(DIVERSE3 or DIVERSE2) to predict drug responses from data of cell lines, drugs, and gene interactions. DIVERSE integrates the data sources systematically, in a step-wise manner, examining the importance of each added data set in turn. More specifically, we sequentially integrate five different data sets, which have not all been combined in earlier bioinformatic methods for predicting drug responses. Empirical experiments show that DIVERSE clearly outperformed five other methods including three state-of-the-art approaches, under cross-validation, particularly in out-of-matrix prediction, which is closer to the setting of real use cases and more challenging than simpler in-matrix prediction. Additionally, case studies for discovering new drugs further confirmed the performance advantage of DIVERSE.

Scalable Probabilistic Matrix Factorization with Graph-Based Priors

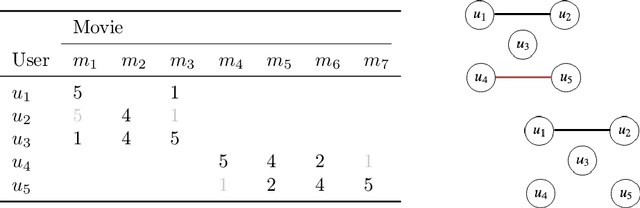
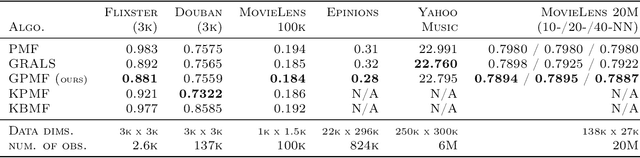
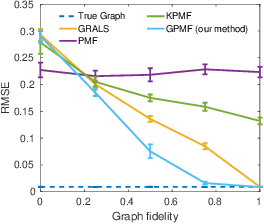
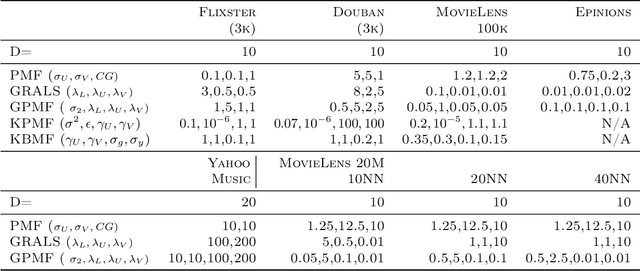
In matrix factorization, available graph side-information may not be well suited for the matrix completion problem, having edges that disagree with the latent-feature relations learnt from the incomplete data matrix. We show that removing these $\textit{contested}$ edges improves prediction accuracy and scalability. We identify the contested edges through a highly-efficient graphical lasso approximation. The identification and removal of contested edges adds no computational complexity to state-of-the-art graph-regularized matrix factorization, remaining linear with respect to the number of non-zeros. Computational load even decreases proportional to the number of edges removed. Formulating a probabilistic generative model and using expectation maximization to extend graph-regularised alternating least squares (GRALS) guarantees convergence. Rich simulated experiments illustrate the desired properties of the resulting algorithm. On real data experiments we demonstrate improved prediction accuracy with fewer graph edges (empirical evidence that graph side-information is often inaccurate). A 300 thousand dimensional graph with three million edges (Yahoo music side-information) can be analyzed in under ten minutes on a standard laptop computer demonstrating the efficiency of our graph update.

AttentionXML: Extreme Multi-Label Text Classification with Multi-Label Attention Based Recurrent Neural Networks

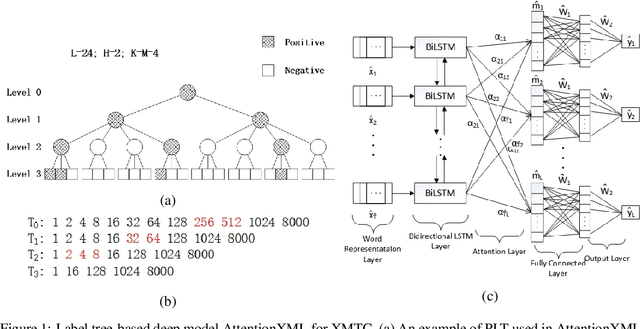
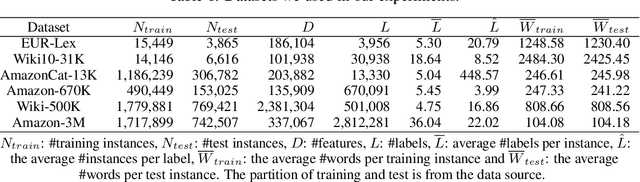
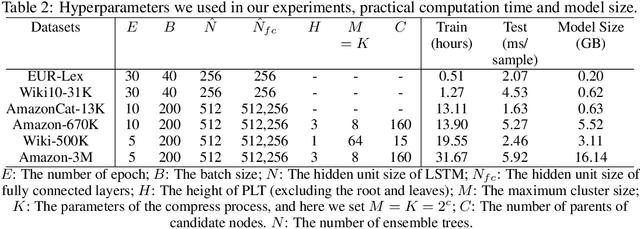
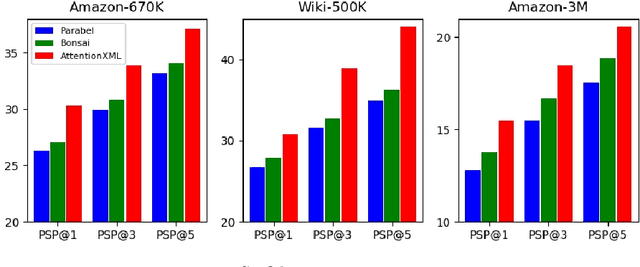
Extreme multi-label text classification (XMTC) is a task for tagging each given text with the most relevant multiple labels from an extremely large-scale label set. This task can be found in many applications, such as product categorization,web page tagging, news annotation and so on. Many methods have been proposed so far for solving XMTC, while most of the existing methods use traditional bag-of-words (BOW) representation, ignoring word context as well as deep semantic information. XML-CNN, a state-of-the-art deep learning-based method, uses convolutional neural network (CNN) with dynamic pooling to process the text, going beyond the BOW-based appraoches but failing to capture 1) the long-distance dependency among words and 2) different levels of importance of a word for each label. We propose a new deep learning-based method, AttentionXML, which uses bidirectional long short-term memory (LSTM) and a multi-label attention mechanism for solving the above 1st and 2nd problems, respectively. We empirically compared AttentionXML with other six state-of-the-art methods over five benchmark datasets. AttentionXML outperformed all competing methods under all experimental settings except only a couple of cases. In addition, a consensus ensemble of AttentionXML with the second best method, Parabel, could further improve the performance over all five benchmark datasets.

Convex Coupled Matrix and Tensor Completion

We propose a set of convex low rank inducing norms for a coupled matrices and tensors (hereafter coupled tensors), which shares information between matrices and tensors through common modes. More specifically, we propose a mixture of the overlapped trace norm and the latent norms with the matrix trace norm, and then, we propose a new completion algorithm based on the proposed norms. A key advantage of the proposed norms is that it is convex and can find a globally optimal solution, while existing methods for coupled learning are non-convex. Furthermore, we analyze the excess risk bounds of the completion model regularized by our proposed norms which show that our proposed norms can exploit the low rankness of coupled tensors leading to better bounds compared to uncoupled norms. Through synthetic and real-world data experiments, we show that the proposed completion algorithm compares favorably with existing completion algorithms.

Learning on Hypergraphs with Sparsity

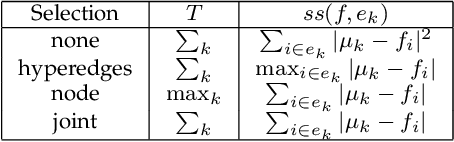
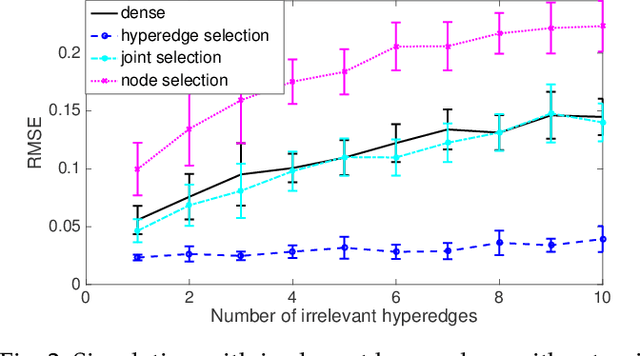
Hypergraph is a general way of representing high-order relations on a set of objects. It is a generalization of graph, in which only pairwise relations can be represented. It finds applications in various domains where relationships of more than two objects are observed. On a hypergraph, as a generalization of graph, one wishes to learn a smooth function with respect to its topology. A fundamental issue is to find suitable smoothness measures of functions on the nodes of a graph/hypergraph. We show a general framework that generalizes previously proposed smoothness measures and also gives rise to new ones. To address the problem of irrelevant or noisy data, we wish to incorporate sparse learning framework into learning on hypergraphs. We propose sparsely smooth formulations that learn smooth functions and induce sparsity on hypergraphs at both hyperedge and node levels. We show their properties and sparse support recovery results. We conduct experiments to show that our sparsely smooth models have benefits to irrelevant and noisy data, and usually give similar or improved performances compared to dense models.

Ultra High-Dimensional Nonlinear Feature Selection for Big Biological Data

Machine learning methods are used to discover complex nonlinear relationships in biological and medical data. However, sophisticated learning models are computationally unfeasible for data with millions of features. Here we introduce the first feature selection method for nonlinear learning problems that can scale up to large, ultra-high dimensional biological data. More specifically, we scale up the novel Hilbert-Schmidt Independence Criterion Lasso (HSIC Lasso) to handle millions of features with tens of thousand samples. The proposed method is guaranteed to find an optimal subset of maximally predictive features with minimal redundancy, yielding higher predictive power and improved interpretability. Its effectiveness is demonstrated through applications to classify phenotypes based on module expression in human prostate cancer patients and to detect enzymes among protein structures. We achieve high accuracy with as few as 20 out of one million features --- a dimensionality reduction of 99.998%. Our algorithm can be implemented on commodity cloud computing platforms. The dramatic reduction of features may lead to the ubiquitous deployment of sophisticated prediction models in mobile health care applications.