RT-Focuser: A Real-Time Lightweight Model for Edge-side Image Deblurring

Motion blur caused by camera or object movement severely degrades image quality and poses challenges for real-time applications such as autonomous driving, UAV perception, and medical imaging. In this paper, a lightweight U-shaped network tailored for real-time deblurring is presented and named RT-Focuser. To balance speed and accuracy, we design three key components: Lightweight Deblurring Block (LD) for edge-aware feature extraction, Multi-Level Integrated Aggregation module (MLIA) for encoder integration, and Cross-source Fusion Block (X-Fuse) for progressive decoder refinement. Trained on a single blurred input, RT-Focuser achieves 30.67 dB PSNR with only 5.85M parameters and 15.76 GMACs. It runs 6ms per frame on GPU and mobile, exceeds 140 FPS on both, showing strong potential for deployment on the edge. The official code and usage are available on: https://github.com/ReaganWu/RT-Focuser.

Noise-robust Contrastive Learning for Critical Transition Detection in Dynamical Systems

Detecting critical transitions in complex, noisy time-series data is a fundamental challenge across science and engineering. Such transitions may be anticipated by the emergence of a low-dimensional order parameter, whose signature is often masked by high-amplitude stochastic variability. Standard contrastive learning approaches based on deep neural networks, while promising for detecting critical transitions, are often overparameterized and sensitive to irrelevant noise, leading to inaccurate identification of critical points. To address these limitations, we propose a neural network architecture, constructed using singular value decomposition technique, together with a strictly semi-orthogonality-constrained training algorithm, to enhance the performance of traditional contrastive learning. Extensive experiments demonstrate that the proposed method matches the performance of traditional contrastive learning techniques in identifying critical transitions, yet is considerably more lightweight and markedly more resistant to noise.

Constants of motion network revisited

Discovering constants of motion is meaningful in helping understand the dynamical systems, but inevitably needs proficient mathematical skills and keen analytical capabilities. With the prevalence of deep learning, methods employing neural networks, such as Constant Of Motion nETwork (COMET), are promising in handling this scientific problem. Although the COMET method can produce better predictions on dynamics by exploiting the discovered constants of motion, there is still plenty of room to sharpen it. In this paper, we propose a novel neural network architecture, built using the singular-value-decomposition (SVD) technique, and a two-phase training algorithm to improve the performance of COMET. Extensive experiments show that our approach not only retains the advantages of COMET, such as applying to non-Hamiltonian systems and indicating the number of constants of motion, but also can be more lightweight and noise-robust than COMET.

Spectrum Gaussian Processes Based On Tunable Basis Functions

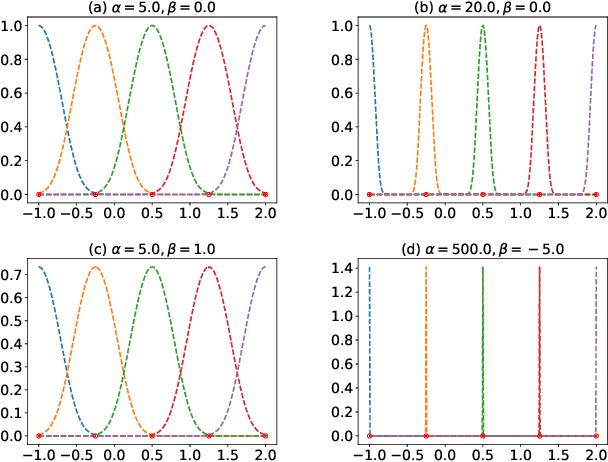
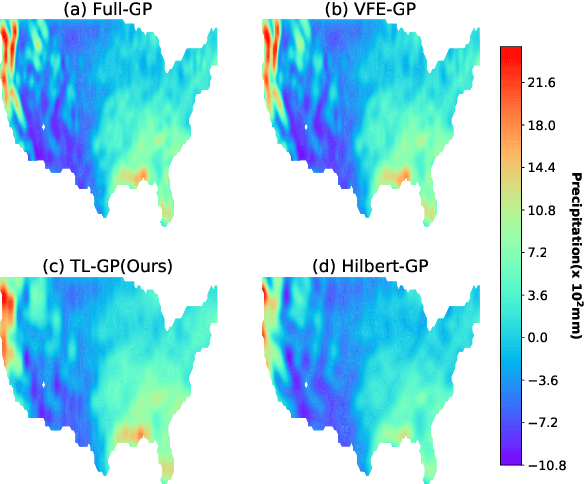
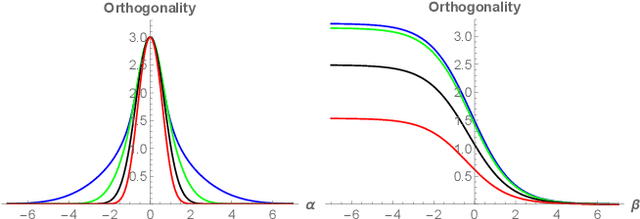
Spectral approximation and variational inducing learning for the Gaussian process are two popular methods to reduce computational complexity. However, in previous research, those methods always tend to adopt the orthonormal basis functions, such as eigenvectors in the Hilbert space, in the spectrum method, or decoupled orthogonal components in the variational framework. In this paper, inspired by quantum physics, we introduce a novel basis function, which is tunable, local and bounded, to approximate the kernel function in the Gaussian process. There are two adjustable parameters in these functions, which control their orthogonality to each other and limit their boundedness. And we conduct extensive experiments on open-source datasets to testify its performance. Compared to several state-of-the-art methods, it turns out that the proposed method can obtain satisfactory or even better results, especially with poorly chosen kernel functions.

Sparse Gaussian Process Based On Hat Basis Functions

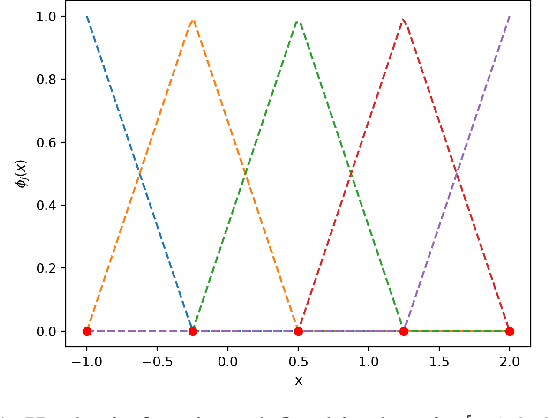
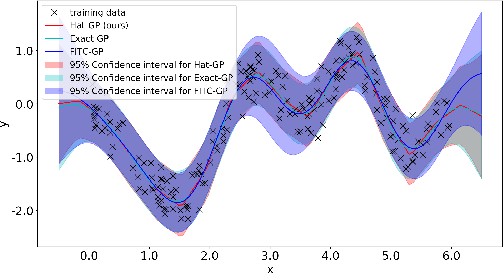
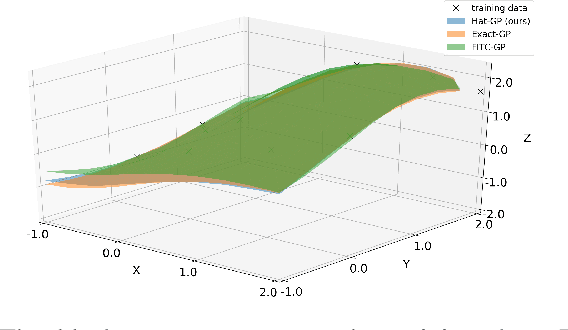
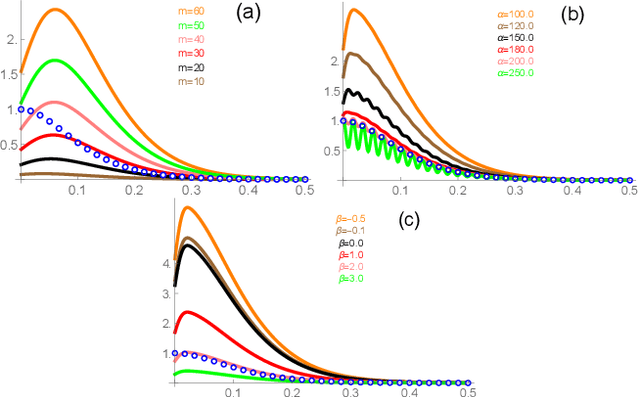
Gaussian process is one of the most popular non-parametric Bayesian methodologies for modeling the regression problem. It is completely determined by its mean and covariance functions. And its linear property makes it relatively straightforward to solve the prediction problem. Although Gaussian process has been successfully applied in many fields, it is still not enough to deal with physical systems that satisfy inequality constraints. This issue has been addressed by the so-called constrained Gaussian process in recent years. In this paper, we extend the core ideas of constrained Gaussian process. According to the range of training or test data, we redefine the hat basis functions mentioned in the constrained Gaussian process. Based on hat basis functions, we propose a new sparse Gaussian process method to solve the unconstrained regression problem. Similar to the exact Gaussian process and Gaussian process with Fully Independent Training Conditional approximation, our method obtains satisfactory approximate results on open-source datasets or analytical functions. In terms of performance, the proposed method reduces the overall computational complexity from $O(n^{3})$ computation in exact Gaussian process to $O(nm^{2})$ with $m$ hat basis functions and $n$ training data points.