Tor Lattimore
Gated Linear Networks
Sep 30, 2019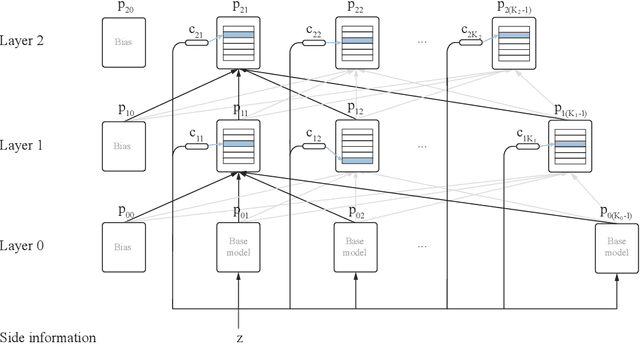
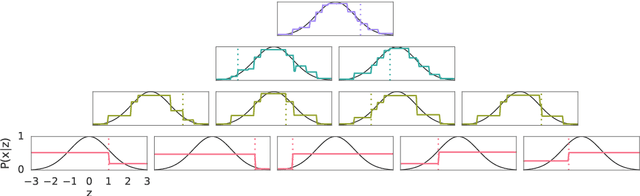
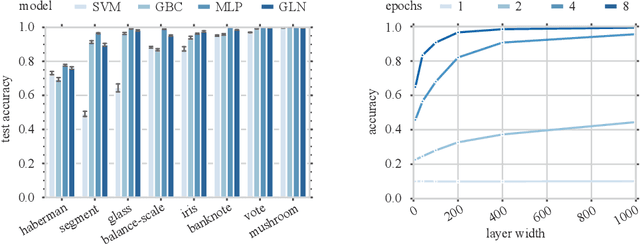
Abstract:This paper presents a family of backpropagation-free neural architectures, Gated Linear Networks (GLNs),that are well suited to online learning applications where sample efficiency is of paramount importance. The impressive empirical performance of these architectures has long been known within the data compression community, but a theoretically satisfying explanation as to how and why they perform so well has proven difficult. What distinguishes these architectures from other neural systems is the distributed and local nature of their credit assignment mechanism; each neuron directly predicts the target and has its own set of hard-gated weights that are locally adapted via online convex optimization. By providing an interpretation, generalization and subsequent theoretical analysis, we show that sufficiently large GLNs are universal in a strong sense: not only can they model any compactly supported, continuous density function to arbitrary accuracy, but that any choice of no-regret online convex optimization technique will provably converge to the correct solution with enough data. Empirically we show a collection of single-pass learning results on established machine learning benchmarks that are competitive with results obtained with general purpose batch learning techniques.
Behaviour Suite for Reinforcement Learning
Aug 13, 2019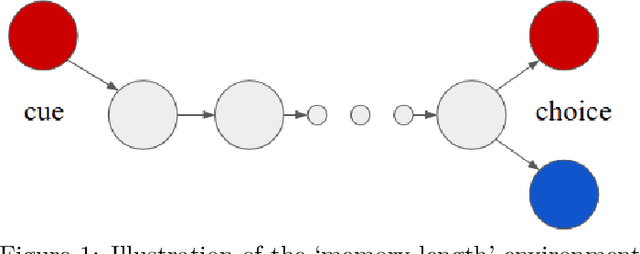
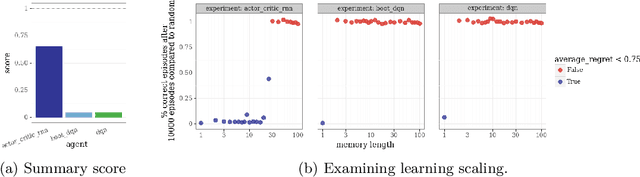
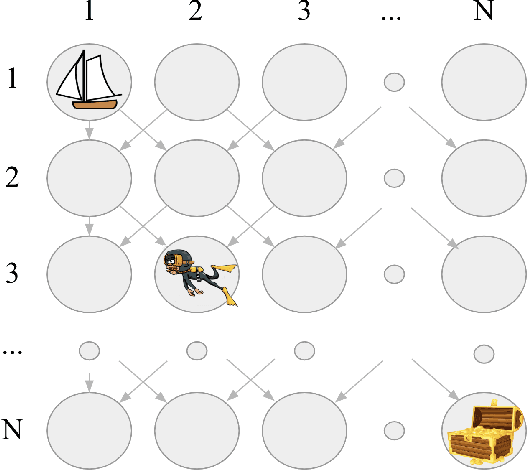
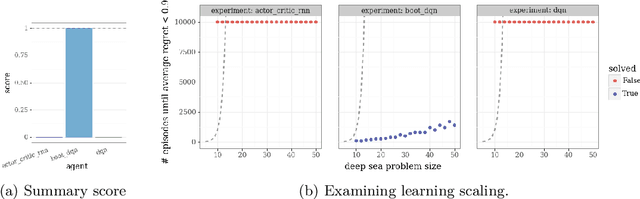
Abstract:This paper introduces the Behaviour Suite for Reinforcement Learning, or bsuite for short. bsuite is a collection of carefully-designed experiments that investigate core capabilities of reinforcement learning (RL) agents with two objectives. First, to collect clear, informative and scalable problems that capture key issues in the design of general and efficient learning algorithms. Second, to study agent behaviour through their performance on these shared benchmarks. To complement this effort, we open source github.com/deepmind/bsuite, which automates evaluation and analysis of any agent on bsuite. This library facilitates reproducible and accessible research on the core issues in RL, and ultimately the design of superior learning algorithms. Our code is Python, and easy to use within existing projects. We include examples with OpenAI Baselines, Dopamine as well as new reference implementations. Going forward, we hope to incorporate more excellent experiments from the research community, and commit to a periodic review of bsuite from a committee of prominent researchers.
Iterative Budgeted Exponential Search
Jul 30, 2019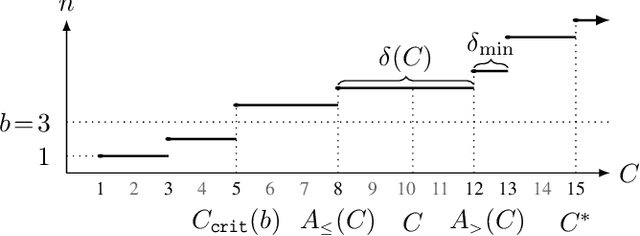
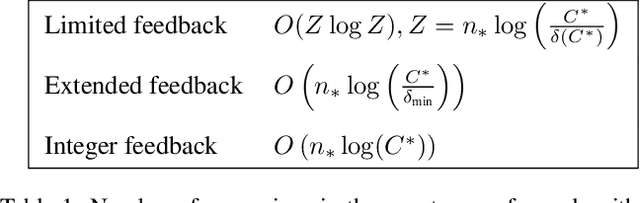
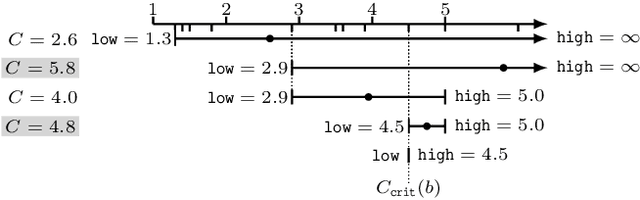
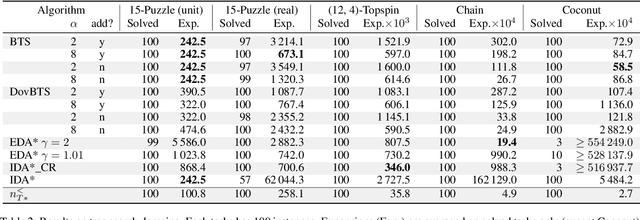
Abstract:We tackle two long-standing problems related to re-expansions in heuristic search algorithms. For graph search, A* can require $\Omega(2^{n})$ expansions, where $n$ is the number of states within the final $f$ bound. Existing algorithms that address this problem like B and B' improve this bound to $\Omega(n^2)$. For tree search, IDA* can also require $\Omega(n^2)$ expansions. We describe a new algorithmic framework that iteratively controls an expansion budget and solution cost limit, giving rise to new graph and tree search algorithms for which the number of expansions is $O(n \log C)$, where $C$ is the optimal solution cost. Our experiments show that the new algorithms are robust in scenarios where existing algorithms fail. In the case of tree search, our new algorithms have no overhead over IDA* in scenarios to which IDA* is well suited and can therefore be recommended as a general replacement for IDA*.
Exploration by Optimisation in Partial Monitoring
Jul 24, 2019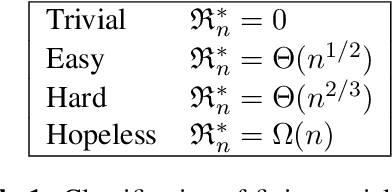
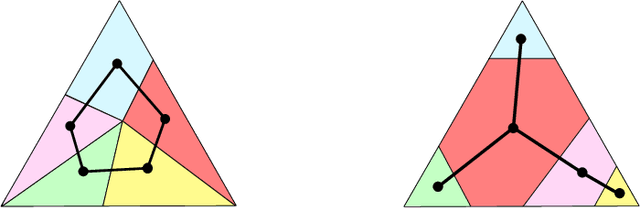

Abstract:We provide a simple and efficient algorithm for adversarial $k$-action $d$-outcome non-degenerate locally observable partial monitoring game for which the $n$-round minimax regret is bounded by $6(d+1) k^{3/2} \sqrt{n \log(k)}$, matching the best known information-theoretic upper bound. The same algorithm also achieves near-optimal regret for full information, bandit and globally observable games.
Zooming Cautiously: Linear-Memory Heuristic Search With Node Expansion Guarantees
Jun 07, 2019
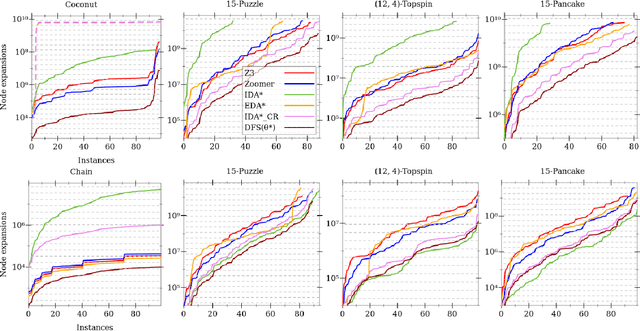

Abstract:We introduce and analyze two parameter-free linear-memory tree search algorithms. Under mild assumptions we prove our algorithms are guaranteed to perform only a logarithmic factor more node expansions than A* when the search space is a tree. Previously, the best guarantee for a linear-memory algorithm under similar assumptions was achieved by IDA*, which in the worst case expands quadratically more nodes than in its last iteration. Empirical results support the theory and demonstrate the practicality and robustness of our algorithms. Furthermore, they are fast and easy to implement.
Connections Between Mirror Descent, Thompson Sampling and the Information Ratio
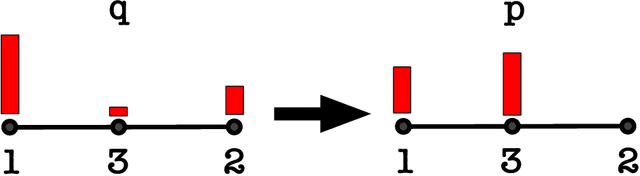
May 28, 2019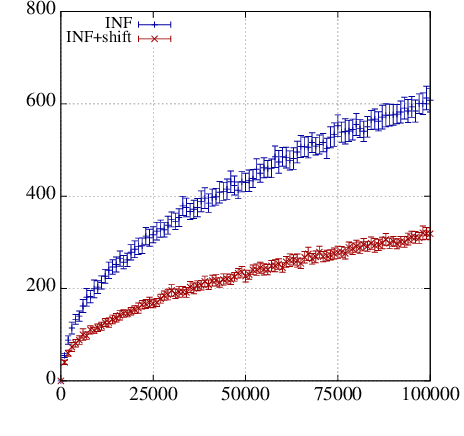
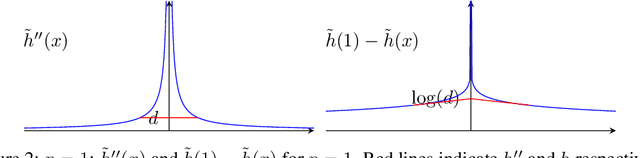
Abstract:The information-theoretic analysis by Russo and Van Roy (2014) in combination with minimax duality has proved a powerful tool for the analysis of online learning algorithms in full and partial information settings. In most applications there is a tantalising similarity to the classical analysis based on mirror descent. We make a formal connection, showing that the information-theoretic bounds in most applications can be derived from existing techniques for online convex optimisation. Besides this, for $k$-armed adversarial bandits we provide an efficient algorithm with regret that matches the best information-theoretic upper bound and improve best known regret guarantees for online linear optimisation on $\ell_p$-balls and bandits with graph feedback.
Degenerate Feedback Loops in Recommender Systems
Mar 27, 2019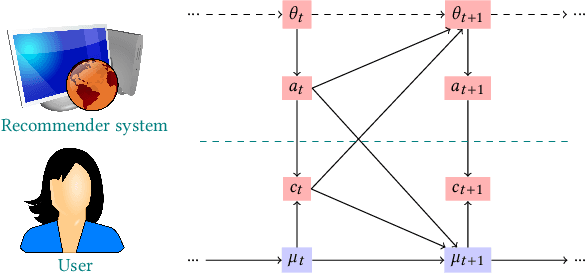
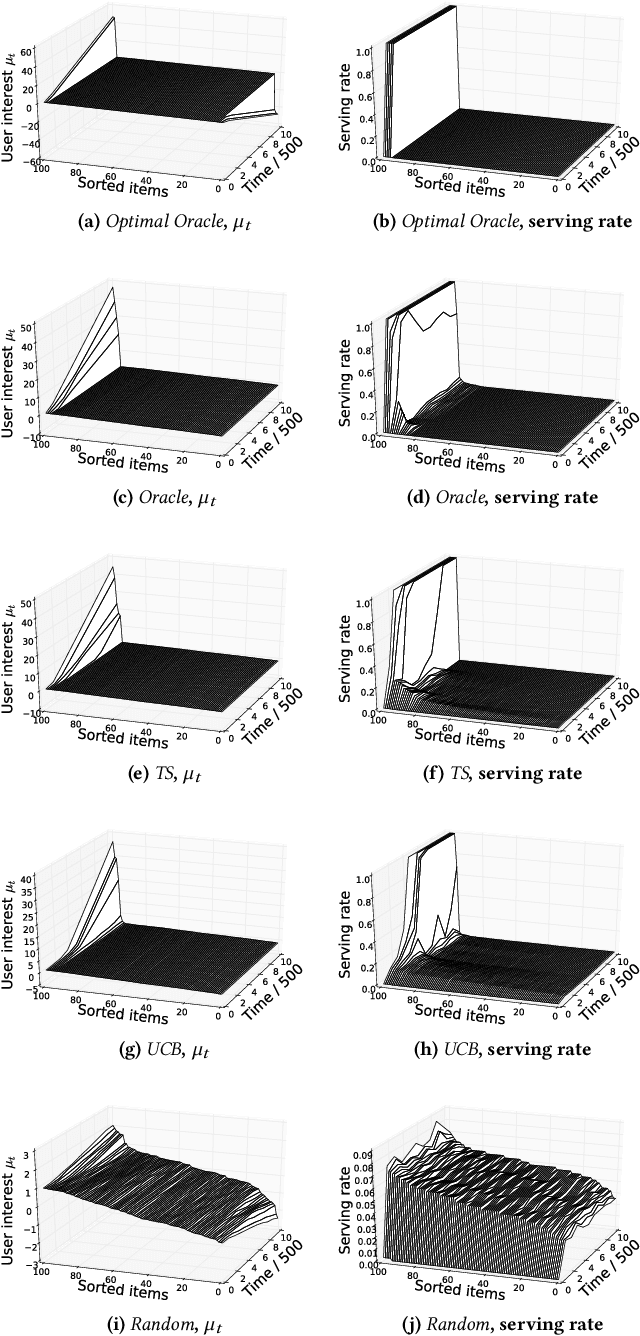
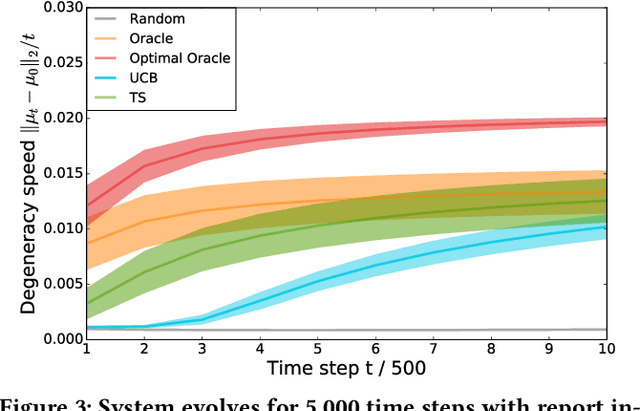
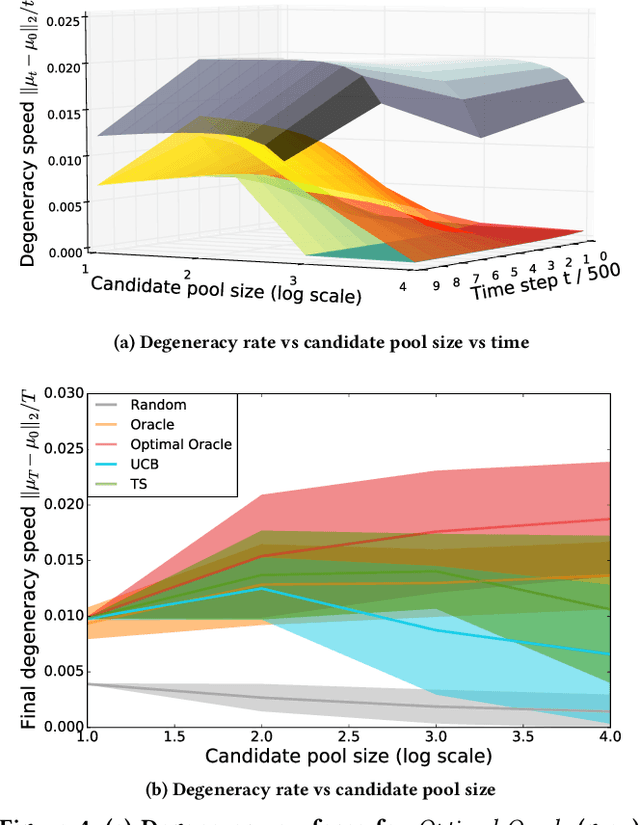
Abstract:Machine learning is used extensively in recommender systems deployed in products. The decisions made by these systems can influence user beliefs and preferences which in turn affect the feedback the learning system receives - thus creating a feedback loop. This phenomenon can give rise to the so-called "echo chambers" or "filter bubbles" that have user and societal implications. In this paper, we provide a novel theoretical analysis that examines both the role of user dynamics and the behavior of recommender systems, disentangling the echo chamber from the filter bubble effect. In addition, we offer practical solutions to slow down system degeneracy. Our study contributes toward understanding and developing solutions to commonly cited issues in the complex temporal scenario, an area that is still largely unexplored.
Adaptivity, Variance and Separation for Adversarial Bandits
Mar 19, 2019
Abstract:We make three contributions to the theory of k-armed adversarial bandits. First, we prove a first-order bound for a modified variant of the INF strategy by Audibert and Bubeck [2009], without sacrificing worst case optimality or modifying the loss estimators. Second, we provide a variance analysis for algorithms based on follow the regularised leader, showing that without adaptation the variance of the regret is typically {\Omega}(n^2) where n is the horizon. Finally, we study bounds that depend on the degree of separation of the arms, generalising the results by Cowan and Katehakis [2015] from the stochastic setting to the adversarial and improving the result of Seldin and Slivkins [2014] by a factor of log(n)/log(log(n)).
An Information-Theoretic Approach to Minimax Regret in Partial Monitoring
Feb 01, 2019
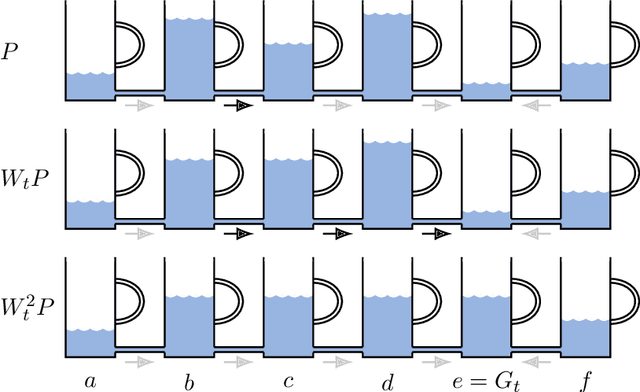

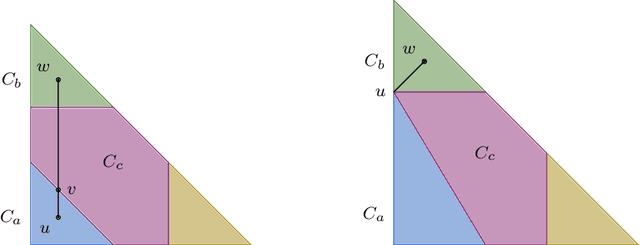
Abstract:We prove a new minimax theorem connecting the worst-case Bayesian regret and minimax regret under partial monitoring with no assumptions on the space of signals or decisions of the adversary. We then generalise the information-theoretic tools of Russo and Van Roy (2016) for proving Bayesian regret bounds and combine them with the minimax theorem to derive minimax regret bounds for various partial monitoring settings. The highlight is a clean analysis of `non-degenerate easy' and `hard' finite partial monitoring, with new regret bounds that are independent of arbitrarily large game-dependent constants. The power of the generalised machinery is further demonstrated by proving that the minimax regret for k-armed adversarial bandits is at most sqrt{2kn}, improving on existing results by a factor of 2. Finally, we provide a simple analysis of the cops and robbers game, also improving best known constants.
A Geometric Perspective on Optimal Representations for Reinforcement Learning
Jan 31, 2019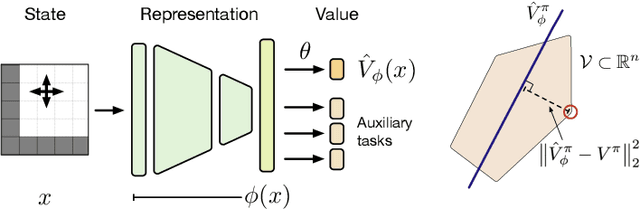
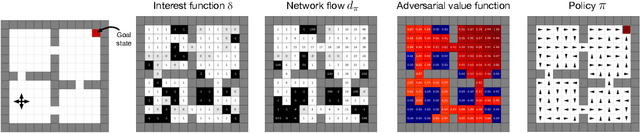
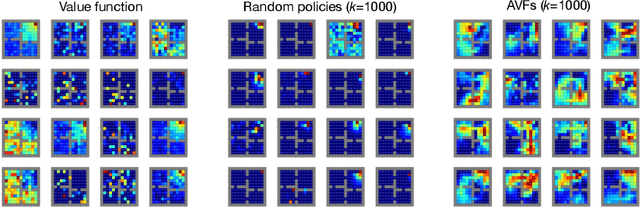
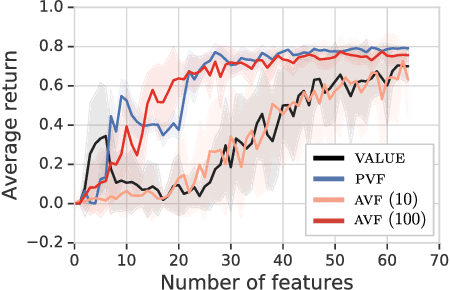
Abstract:This paper proposes a new approach to representation learning based on geometric properties of the space of value functions. We study a two-part approximation of the value function: a nonlinear map from states to vectors, or representation, followed by a linear map from vectors to values. Our formulation considers adapting the representation to minimize the (linear) approximation of the value function of all stationary policies for a given environment. We show that this optimization reduces to making accurate predictions regarding a special class of value functions which we call adversarial value functions (AVFs). We argue that these AVFs make excellent auxiliary tasks, and use them to construct a loss which can be efficiently minimized to find a near-optimal representation for reinforcement learning. We highlight characteristics of the method in a series of experiments on the four-room domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge