A Formalism for Optimal Search with Dynamic Heuristics

While most heuristics studied in heuristic search depend only on the state, some accumulate information during search and thus also depend on the search history. Various existing approaches use such dynamic heuristics in $\mathrm{A}^*$-like algorithms and appeal to classic results for $\mathrm{A}^*$ to show optimality. However, doing so ignores the complexities of searching with a mutable heuristic. In this paper we formalize the idea of dynamic heuristics and use them in a generic algorithm framework. We study a particular instantiation that models $\mathrm{A}^*$ with dynamic heuristics and show general optimality results. Finally we show how existing approaches from classical planning can be viewed as special cases of this instantiation, making it possible to directly apply our optimality results.

Pseudo-Boolean Proof Logging for Optimal Classical Planning

We introduce lower-bound certificates for classical planning tasks, which can be used to prove the unsolvability of a task or the optimality of a plan in a way that can be verified by an independent third party. We describe a general framework for generating lower-bound certificates based on pseudo-Boolean constraints, which is agnostic to the planning algorithm used. As a case study, we show how to modify the $A^{*}$ algorithm to produce proofs of optimality with modest overhead, using pattern database heuristics and $h^\textit{max}$ as concrete examples. The same proof logging approach works for any heuristic whose inferences can be efficiently expressed as reasoning over pseudo-Boolean constraints.

Higher-Dimensional Potential Heuristics for Optimal Classical Planning

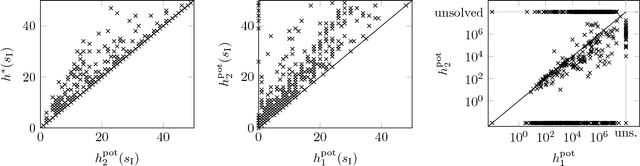
Potential heuristics for state-space search are defined as weighted sums over simple state features. Atomic features consider the value of a single state variable in a factored state representation, while binary features consider joint assignments to two state variables. Previous work showed that the set of all admissible and consistent potential heuristics using atomic features can be characterized by a compact set of linear constraints. We generalize this result to binary features and prove a hardness result for features of higher dimension. Furthermore, we prove a tractability result based on the treewidth of a new graphical structure we call the context-dependency graph. Finally, we study the relationship of potential heuristics to transition cost partitioning. Experimental results show that binary potential heuristics are significantly more informative than the previously considered atomic ones.

Iterative Budgeted Exponential Search

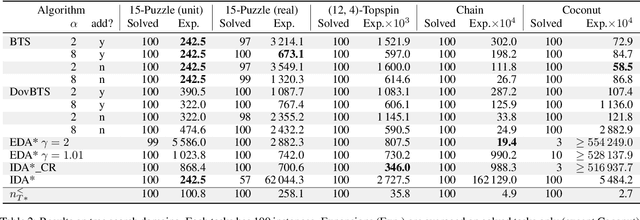
We tackle two long-standing problems related to re-expansions in heuristic search algorithms. For graph search, A* can require $\Omega(2^{n})$ expansions, where $n$ is the number of states within the final $f$ bound. Existing algorithms that address this problem like B and B' improve this bound to $\Omega(n^2)$. For tree search, IDA* can also require $\Omega(n^2)$ expansions. We describe a new algorithmic framework that iteratively controls an expansion budget and solution cost limit, giving rise to new graph and tree search algorithms for which the number of expansions is $O(n \log C)$, where $C$ is the optimal solution cost. Our experiments show that the new algorithms are robust in scenarios where existing algorithms fail. In the case of tree search, our new algorithms have no overhead over IDA* in scenarios to which IDA* is well suited and can therefore be recommended as a general replacement for IDA*.

Exponential-Binary State-Space Search

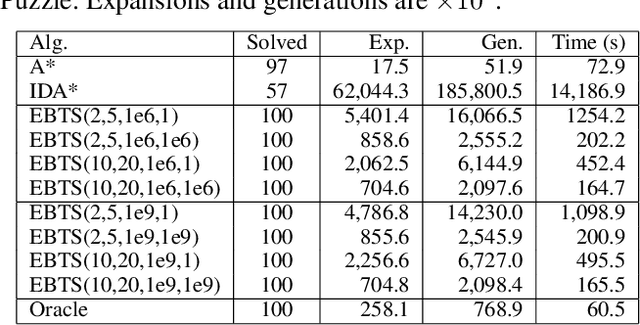
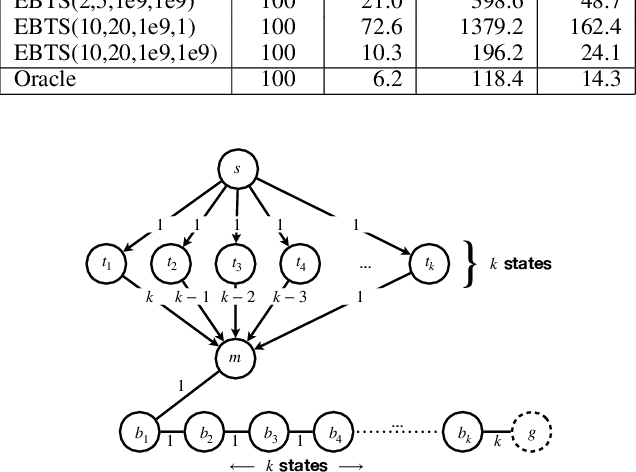
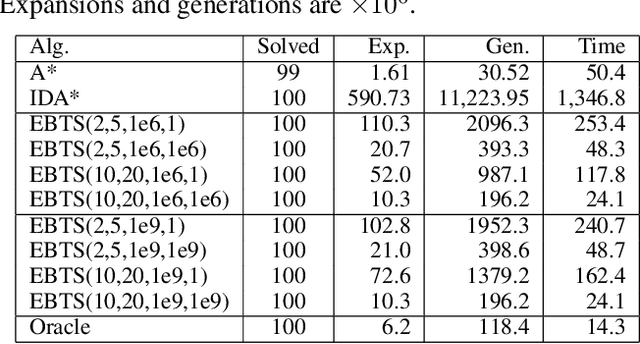
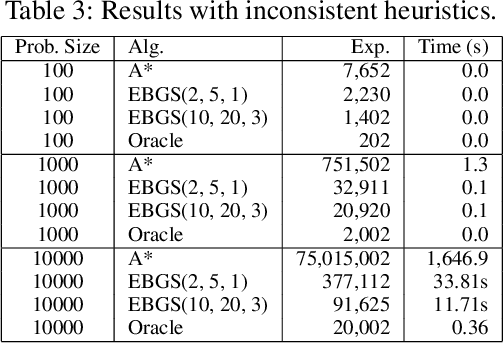
Iterative deepening search is used in applications where the best cost bound for state-space search is unknown. The iterative deepening process is used to avoid overshooting the appropriate cost bound and doing too much work as a result. However, iterative deepening search also does too much work if the cost bound grows too slowly. This paper proposes a new framework for iterative deepening search called exponential-binary state-space search. The approach interleaves exponential and binary searches to find the desired cost bound, reducing the worst-case overhead from polynomial to logarithmic. Exponential-binary search can be used with bounded depth-first search to improve the worst-case performance of IDA* and with breadth-first heuristic search to improve the worst-case performance of search with inconsistent heuristics.

Message-Based Web Service Composition, Integrity Constraints, and Planning under Uncertainty: A New Connection

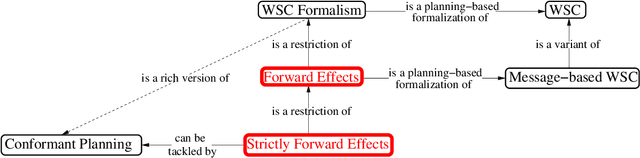
Thanks to recent advances, AI Planning has become the underlying technique for several applications. Figuring prominently among these is automated Web Service Composition (WSC) at the "capability" level, where services are described in terms of preconditions and effects over ontological concepts. A key issue in addressing WSC as planning is that ontologies are not only formal vocabularies; they also axiomatize the possible relationships between concepts. Such axioms correspond to what has been termed "integrity constraints" in the actions and change literature, and applying a web service is essentially a belief update operation. The reasoning required for belief update is known to be harder than reasoning in the ontology itself. The support for belief update is severely limited in current planning tools. Our first contribution consists in identifying an interesting special case of WSC which is both significant and more tractable. The special case, which we term "forward effects", is characterized by the fact that every ramification of a web service application involves at least one new constant generated as output by the web service. We show that, in this setting, the reasoning required for belief update simplifies to standard reasoning in the ontology itself. This relates to, and extends, current notions of "message-based" WSC, where the need for belief update is removed by a strong (often implicit or informal) assumption of "locality" of the individual messages. We clarify the computational properties of the forward effects case, and point out a strong relation to standard notions of planning under uncertainty, suggesting that effective tools for the latter can be successfully adapted to address the former. Furthermore, we identify a significant sub-case, named "strictly forward effects", where an actual compilation into planning under uncertainty exists. This enables us to exploit off-the-shelf planning tools to solve message-based WSC in a general form that involves powerful ontologies, and requires reasoning about partial matches between concepts. We provide empirical evidence that this approach may be quite effective, using Conformant-FF as the underlying planner.