Practical Kernel Tests of Conditional Independence

We describe a data-efficient, kernel-based approach to statistical testing of conditional independence. A major challenge of conditional independence testing, absent in tests of unconditional independence, is to obtain the correct test level (the specified upper bound on the rate of false positives), while still attaining competitive test power. Excess false positives arise due to bias in the test statistic, which is obtained using nonparametric kernel ridge regression. We propose three methods for bias control to correct the test level, based on data splitting, auxiliary data, and (where possible) simpler function classes. We show these combined strategies are effective both for synthetic and real-world data.

Synaptic Weight Distributions Depend on the Geometry of Plasticity

Most learning algorithms in machine learning rely on gradient descent to adjust model parameters, and a growing literature in computational neuroscience leverages these ideas to study synaptic plasticity in the brain. However, the vast majority of this work ignores a critical underlying assumption: the choice of distance for synaptic changes (i.e. the geometry of synaptic plasticity). Gradient descent assumes that the distance is Euclidean, but many other distances are possible, and there is no reason that biology necessarily uses Euclidean geometry. Here, using the theoretical tools provided by mirror descent, we show that, regardless of the loss being minimized, the distribution of synaptic weights will depend on the geometry of synaptic plasticity. We use these results to show that experimentally-observed log-normal weight distributions found in several brain areas are not consistent with standard gradient descent (i.e. a Euclidean geometry), but rather with non-Euclidean distances. Finally, we show that it should be possible to experimentally test for different synaptic geometries by comparing synaptic weight distributions before and after learning. Overall, this work shows that the current paradigm in theoretical work on synaptic plasticity that assumes Euclidean synaptic geometry may be misguided and that it should be possible to experimentally determine the true geometry of synaptic plasticity in the brain.

Efficient Conditionally Invariant Representation Learning

We introduce the Conditional Independence Regression CovariancE (CIRCE), a measure of conditional independence for multivariate continuous-valued variables. CIRCE applies as a regularizer in settings where we wish to learn neural features $\varphi(X)$ of data $X$ to estimate a target $Y$, while being conditionally independent of a distractor $Z$ given $Y$. Both $Z$ and $Y$ are assumed to be continuous-valued but relatively low dimensional, whereas $X$ and its features may be complex and high dimensional. Relevant settings include domain-invariant learning, fairness, and causal learning. The procedure requires just a single ridge regression from $Y$ to kernelized features of $Z$, which can be done in advance. It is then only necessary to enforce independence of $\varphi(X)$ from residuals of this regression, which is possible with attractive estimation properties and consistency guarantees. By contrast, earlier measures of conditional feature dependence require multiple regressions for each step of feature learning, resulting in more severe bias and variance, and greater computational cost. When sufficiently rich features are used, we establish that CIRCE is zero if and only if $\varphi(X) \perp \!\!\! \perp Z \mid Y$. In experiments, we show superior performance to previous methods on challenging benchmarks, including learning conditionally invariant image features.

Towards Biologically Plausible Convolutional Networks

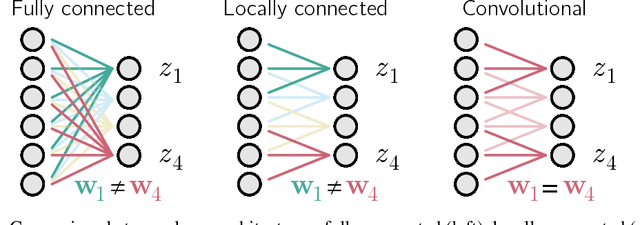
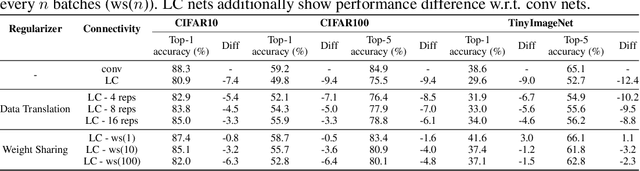
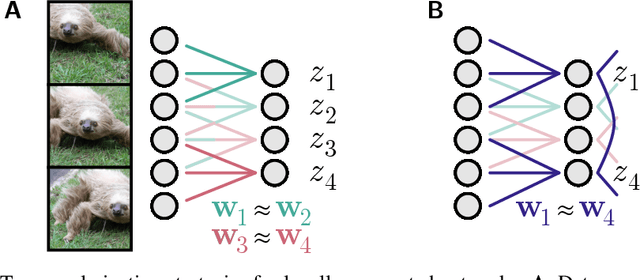
Convolutional networks are ubiquitous in deep learning. They are particularly useful for images, as they reduce the number of parameters, reduce training time, and increase accuracy. However, as a model of the brain they are seriously problematic, since they require weight sharing - something real neurons simply cannot do. Consequently, while neurons in the brain can be locally connected (one of the features of convolutional networks), they cannot be convolutional. Locally connected but non-convolutional networks, however, significantly underperform convolutional ones. This is troublesome for studies that use convolutional networks to explain activity in the visual system. Here we study plausible alternatives to weight sharing that aim at the same regularization principle, which is to make each neuron within a pool react similarly to identical inputs. The most natural way to do that is by showing the network multiple translations of the same image, akin to saccades in animal vision. However, this approach requires many translations, and doesn't remove the performance gap. We propose instead to add lateral connectivity to a locally connected network, and allow learning via Hebbian plasticity. This requires the network to pause occasionally for a sleep-like phase of "weight sharing". This method enables locally connected networks to achieve nearly convolutional performance on ImageNet, thus supporting convolutional networks as a model of the visual stream.

Self-Supervised Learning with Kernel Dependence Maximization

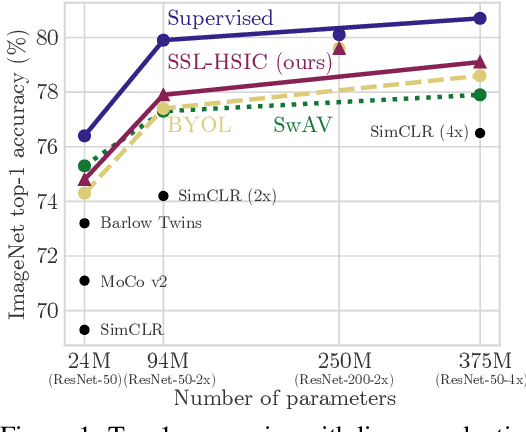
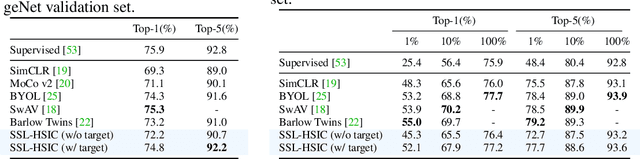
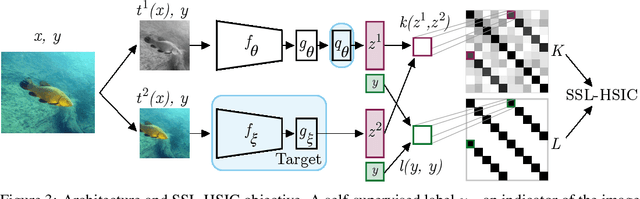
We approach self-supervised learning of image representations from a statistical dependence perspective, proposing Self-Supervised Learning with the Hilbert-Schmidt Independence Criterion (SSL-HSIC). SSL-HSIC maximizes dependence between representations of transformed versions of an image and the image identity, while minimizing the kernelized variance of those features. This self-supervised learning framework yields a new understanding of InfoNCE, a variational lower bound on the mutual information (MI) between different transformations. While the MI itself is known to have pathologies which can result in meaningless representations being learned, its bound is much better behaved: we show that it implicitly approximates SSL-HSIC (with a slightly different regularizer). Our approach also gives us insight into BYOL, since SSL-HSIC similarly learns local neighborhoods of samples. SSL-HSIC allows us to directly optimize statistical dependence in time linear in the batch size, without restrictive data assumptions or indirect mutual information estimators. Trained with or without a target network, SSL-HSIC matches the current state-of-the-art for standard linear evaluation on ImageNet, semi-supervised learning and transfer to other classification and vision tasks such as semantic segmentation, depth estimation and object recognition.

Kernelized information bottleneck leads to biologically plausible 3-factor Hebbian learning in deep networks

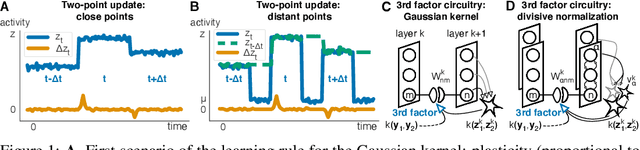
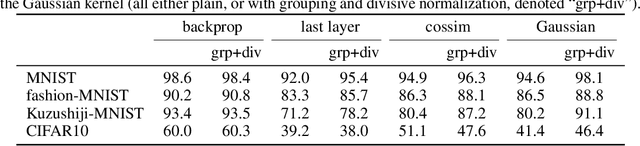
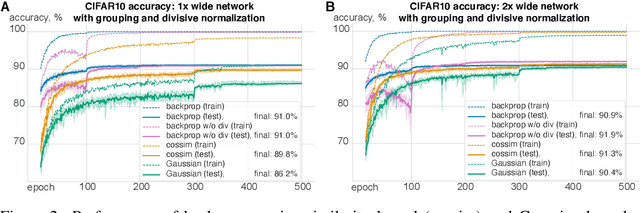
The state-of-the art machine learning approach to training deep neural networks, backpropagation, is implausible for real neural networks: neurons need to know their outgoing weights; training alternates between a forward pass (computation) and a backward pass (learning); and the algorithm needs a large amount of labeled data. Biologically plausible approximations to backpropagation, such as feedback alignment, solve the weight transport problem, but not the other two. Thus, fully biologically plausible learning rules have so far remained elusive. Here we present a family of learning rules that does not suffer from any of these problems. It is motivated by the information bottleneck principle (extended with kernel methods), in which networks learn to squeeze as much information as possible out of the input without sacrificing prediction of the output. The resulting rules have a 3-factor Hebbian structure: they require pre- and post-synaptic firing rates and a global error signal - the third factor - that can be supplied by a neuromodulator. Moreover, they do not require precise labels; instead, they rely on the similarity between the desired outputs. They thus solve all three implausibility issues of backpropagation. Moreover, to obtain good performance on hard problems and retain biologically plausible learning rules, our rules need divisive normalization - a known feature of biological networks. Finally, simulations show that our rule performs nearly as well as backpropagation on image classification tasks.

Working memory facilitates reward-modulated Hebbian learning in recurrent neural networks

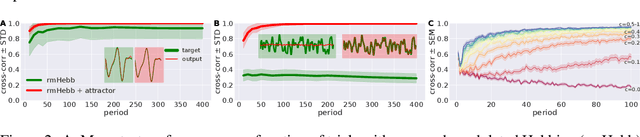
Reservoir computing is a powerful tool to explain how the brain learns temporal sequences, such as movements, but existing learning schemes are either biologically implausible or too inefficient to explain animal performance. We show that a network can learn complicated sequences with a reward-modulated Hebbian learning rule if the network of reservoir neurons is combined with a second network that serves as a dynamic working memory and provides a spatio-temporal backbone signal to the reservoir. In combination with the working memory, reward-modulated Hebbian learning of the readout neurons performs as well as FORCE learning, but with the advantage of a biologically plausible interpretation of both the learning rule and the learning paradigm.

Adaptivity, Variance and Separation for Adversarial Bandits

We make three contributions to the theory of k-armed adversarial bandits. First, we prove a first-order bound for a modified variant of the INF strategy by Audibert and Bubeck [2009], without sacrificing worst case optimality or modifying the loss estimators. Second, we provide a variance analysis for algorithms based on follow the regularised leader, showing that without adaptation the variance of the regret is typically {\Omega}(n^2) where n is the horizon. Finally, we study bounds that depend on the degree of separation of the arms, generalising the results by Cowan and Katehakis [2015] from the stochastic setting to the adversarial and improving the result of Seldin and Slivkins [2014] by a factor of log(n)/log(log(n)).