Heteroskedastic and Imbalanced Deep Learning with Adaptive Regularization

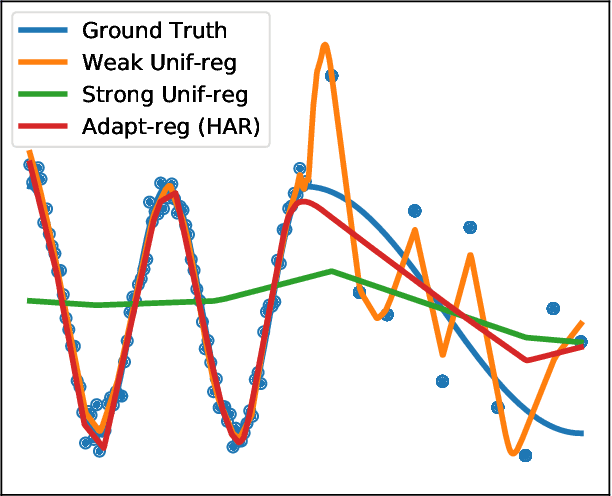
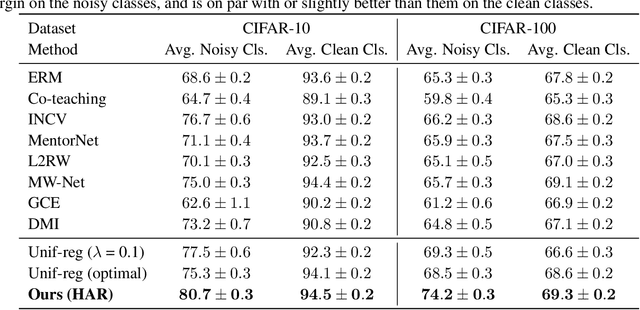
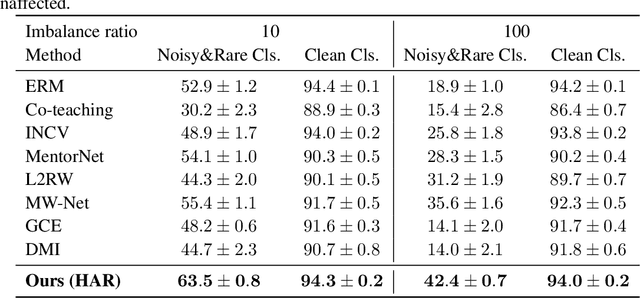
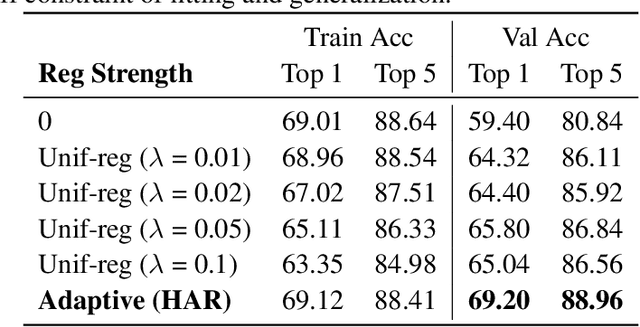
Real-world large-scale datasets are heteroskedastic and imbalanced -- labels have varying levels of uncertainty and label distributions are long-tailed. Heteroskedasticity and imbalance challenge deep learning algorithms due to the difficulty of distinguishing among mislabeled, ambiguous, and rare examples. Addressing heteroskedasticity and imbalance simultaneously is under-explored. We propose a data-dependent regularization technique for heteroskedastic datasets that regularizes different regions of the input space differently. Inspired by the theoretical derivation of the optimal regularization strength in a one-dimensional nonparametric classification setting, our approach adaptively regularizes the data points in higher-uncertainty, lower-density regions more heavily. We test our method on several benchmark tasks, including a real-world heteroskedastic and imbalanced dataset, WebVision. Our experiments corroborate our theory and demonstrate a significant improvement over other methods in noise-robust deep learning.

Active Online Domain Adaptation

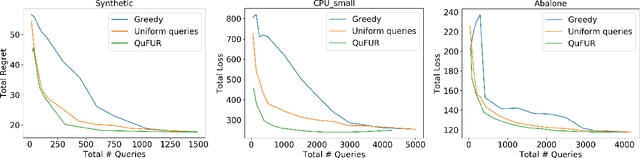
Online machine learning systems need to adapt to domain shifts. Meanwhile, acquiring label at every timestep is expensive. We propose a surprisingly simple algorithm that adaptively balances its regret and its number of label queries in settings where the data streams are from a mixture of hidden domains. For online linear regression with oblivious adversaries, we provide a tight tradeoff that depends on the durations and dimensionalities of the hidden domains. Our algorithm can adaptively deal with interleaving spans of inputs from different domains. We also generalize our results to non-linear regression for hypothesis classes with bounded eluder dimension and adaptive adversaries. Experiments on synthetic and realistic datasets demonstrate that our algorithm achieves lower regret than uniform queries and greedy queries with equal labeling budget.

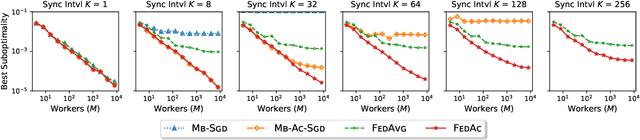
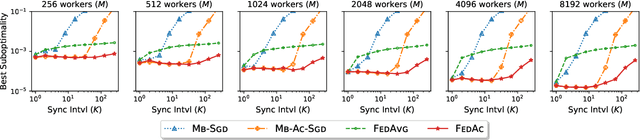
Federated Accelerated Stochastic Gradient Descent

We propose Federated Accelerated Stochastic Gradient Descent (FedAc), a principled acceleration of Federated Averaging (FedAvg, also known as Local SGD) for distributed optimization. FedAc is the first provable acceleration of FedAvg that improves convergence speed and communication efficiency on various types of convex functions. For example, for strongly convex and smooth functions, when using $M$ workers, the previous state-of-the-art FedAvg analysis can achieve a linear speedup in $M$ if given $M$ rounds of synchronization, whereas FedAc only requires $M^{\frac{1}{3}}$ rounds. Moreover, we prove stronger guarantees for FedAc when the objectives are third-order smooth. Our technique is based on a potential-based perturbed iterate analysis, a novel stability analysis of generalized accelerated SGD, and a strategic tradeoff between acceleration and stability.

Shape Matters: Understanding the Implicit Bias of the Noise Covariance

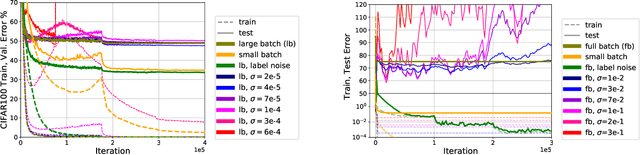
The noise in stochastic gradient descent (SGD) provides a crucial implicit regularization effect for training overparameterized models. Prior theoretical work largely focuses on spherical Gaussian noise, whereas empirical studies demonstrate the phenomenon that parameter-dependent noise -- induced by mini-batches or label perturbation -- is far more effective than Gaussian noise. This paper theoretically characterizes this phenomenon on a quadratically-parameterized model introduced by Vaskevicius et el. and Woodworth et el. We show that in an over-parameterized setting, SGD with label noise recovers the sparse ground-truth with an arbitrary initialization, whereas SGD with Gaussian noise or gradient descent overfits to dense solutions with large norms. Our analysis reveals that parameter-dependent noise introduces a bias towards local minima with smaller noise variance, whereas spherical Gaussian noise does not. Code for our project is publicly available.

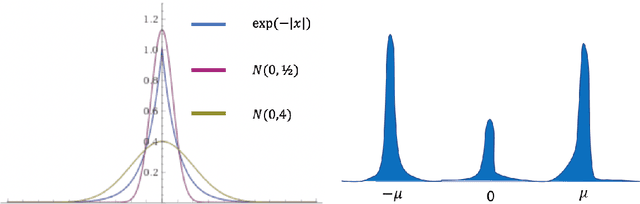
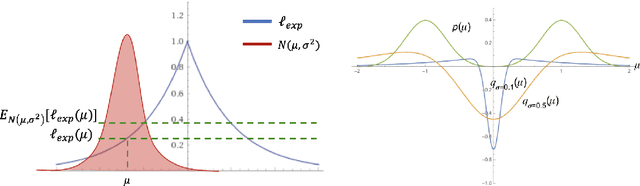
Self-training Avoids Using Spurious Features Under Domain Shift

In unsupervised domain adaptation, existing theory focuses on situations where the source and target domains are close. In practice, conditional entropy minimization and pseudo-labeling work even when the domain shifts are much larger than those analyzed by existing theory. We identify and analyze one particular setting where the domain shift can be large, but these algorithms provably work: certain spurious features correlate with the label in the source domain but are independent of the label in the target. Our analysis considers linear classification where the spurious features are Gaussian and the non-spurious features are a mixture of log-concave distributions. For this setting, we prove that entropy minimization on unlabeled target data will avoid using the spurious feature if initialized with a decently accurate source classifier, even though the objective is non-convex and contains multiple bad local minima using the spurious features. We verify our theory for spurious domain shift tasks on semi-synthetic Celeb-A and MNIST datasets. Our results suggest that practitioners collect and self-train on large, diverse datasets to reduce biases in classifiers even if labeling is impractical.

Model-based Adversarial Meta-Reinforcement Learning

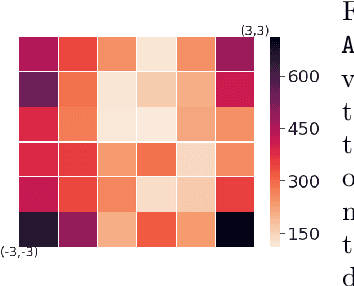
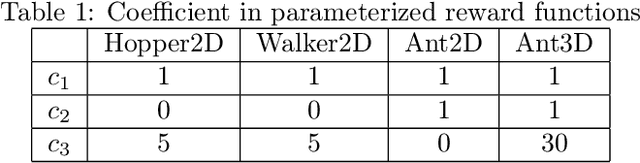
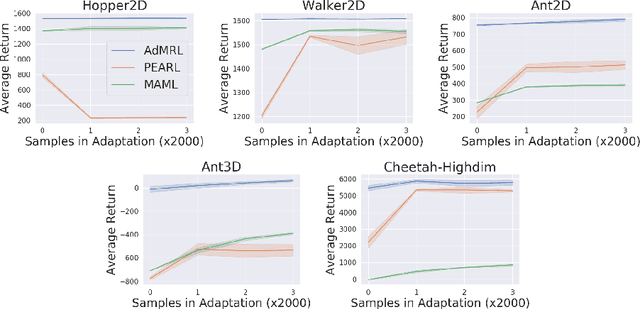
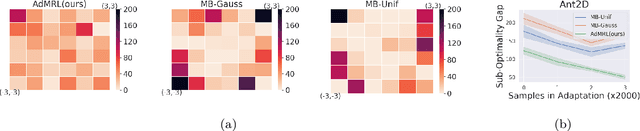
Meta-reinforcement learning (meta-RL) aims to learn from multiple training tasks the ability to adapt efficiently to unseen test tasks. Despite the success, existing meta-RL algorithms are known to be sensitive to the task distribution shift. When the test task distribution is different from the training task distribution, the performance may degrade significantly. To address this issue, this paper proposes Model-based Adversarial Meta-Reinforcement Learning (AdMRL), where we aim to minimize the worst-case sub-optimality gap -- the difference between the optimal return and the return that the algorithm achieves after adaptation -- across all tasks in a family of tasks, with a model-based approach. We propose a minimax objective and optimize it by alternating between learning the dynamics model on a fixed task and finding the adversarial task for the current model -- the task for which the policy induced by the model is maximally suboptimal. Assuming the family of tasks is parameterized, we derive a formula for the gradient of the suboptimality with respect to the task parameters via the implicit function theorem, and show how the gradient estimator can be efficiently implemented by the conjugate gradient method and a novel use of the REINFORCE estimator. We evaluate our approach on several continuous control benchmarks and demonstrate its efficacy in the worst-case performance over all tasks, the generalization power to out-of-distribution tasks, and in training and test time sample efficiency, over existing state-of-the-art meta-RL algorithms.

MOPO: Model-based Offline Policy Optimization

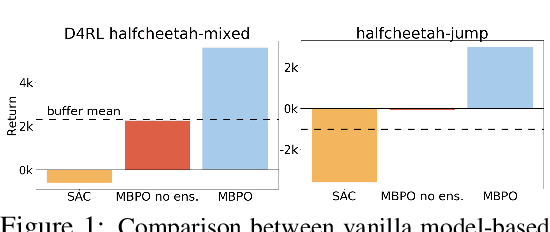
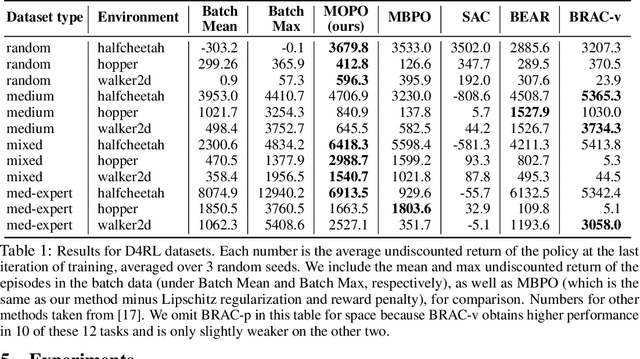
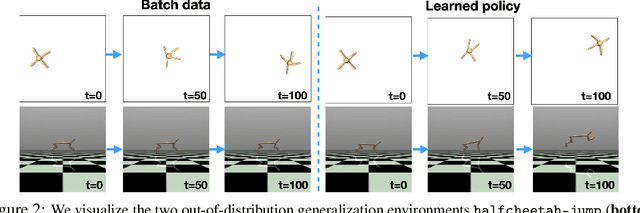
Offline reinforcement learning (RL) refers to the problem of learning policies entirely from a batch of previously collected data. This problem setting is compelling, because it offers the promise of utilizing large, diverse, previously collected datasets to acquire policies without any costly or dangerous active exploration, but it is also exceptionally difficult, due to the distributional shift between the offline training data and the learned policy. While there has been significant progress in model-free offline RL, the most successful prior methods constrain the policy to the support of the data, precluding generalization to new states. In this paper, we observe that an existing model-based RL algorithm on its own already produces significant gains in the offline setting, as compared to model-free approaches, despite not being designed for this setting. However, although many standard model-based RL methods already estimate the uncertainty of their model, they do not by themselves provide a mechanism to avoid the issues associated with distributional shift in the offline setting. We therefore propose to modify existing model-based RL methods to address these issues by casting offline model-based RL into a penalized MDP framework. We theoretically show that, by using this penalized MDP, we are maximizing a lower bound of the return in the true MDP. Based on our theoretical results, we propose a new model-based offline RL algorithm that applies the variance of a Lipschitz-regularized model as a penalty to the reward function. We find that this algorithm outperforms both standard model-based RL methods and existing state-of-the-art model-free offline RL approaches on existing offline RL benchmarks, as well as two challenging continuous control tasks that require generalizing from data collected for a different task.

Robust and On-the-fly Dataset Denoising for Image Classification

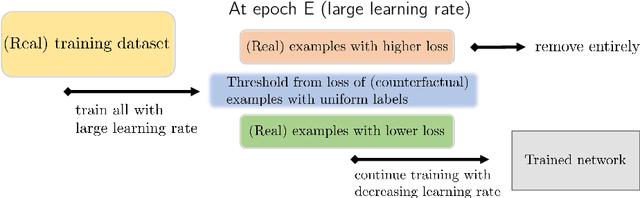
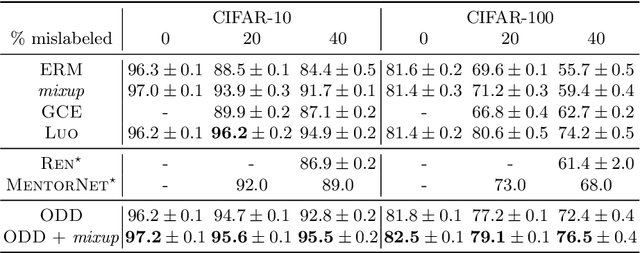
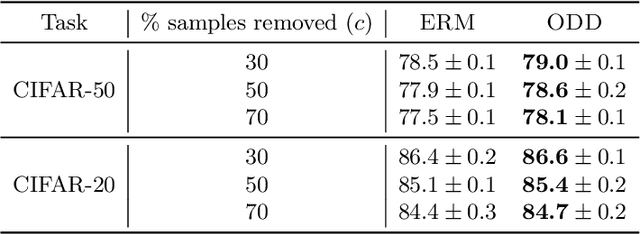
Memorization in over-parameterized neural networks could severely hurt generalization in the presence of mislabeled examples. However, mislabeled examples are hard to avoid in extremely large datasets collected with weak supervision. We address this problem by reasoning counterfactually about the loss distribution of examples with uniform random labels had they were trained with the real examples, and use this information to remove noisy examples from the training set. First, we observe that examples with uniform random labels have higher losses when trained with stochastic gradient descent under large learning rates. Then, we propose to model the loss distribution of the counterfactual examples using only the network parameters, which is able to model such examples with remarkable success. Finally, we propose to remove examples whose loss exceeds a certain quantile of the modeled loss distribution. This leads to On-the-fly Data Denoising (ODD), a simple yet effective algorithm that is robust to mislabeled examples, while introducing almost zero computational overhead compared to standard training. ODD is able to achieve state-of-the-art results on a wide range of datasets including real-world ones such as WebVision and Clothing1M.

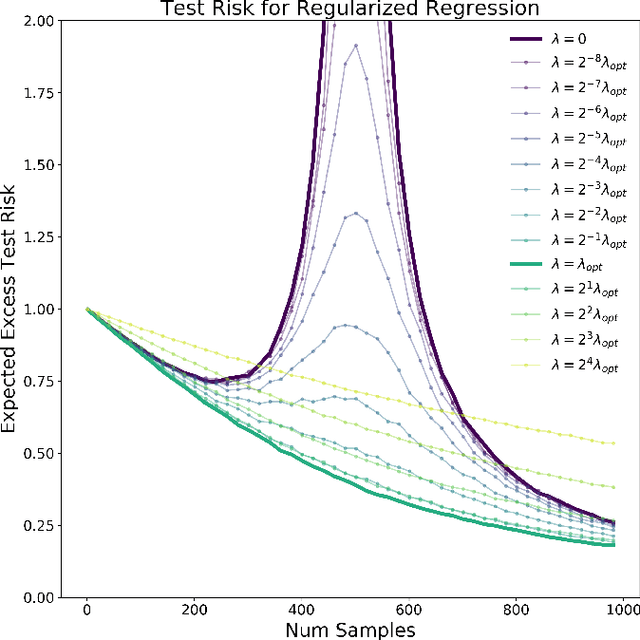
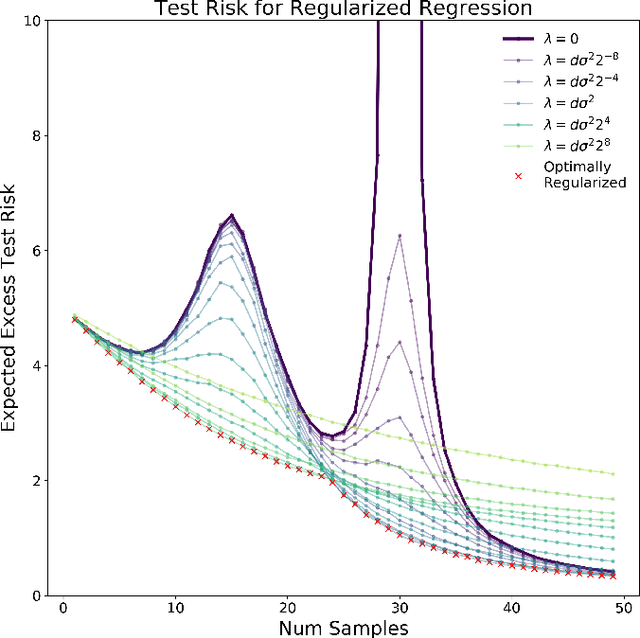
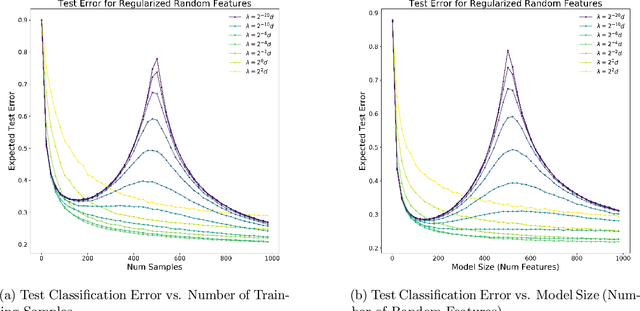
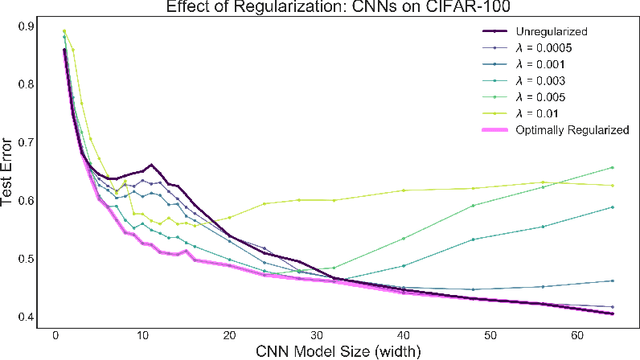
Optimal Regularization Can Mitigate Double Descent

Recent empirical and theoretical studies have shown that many learning algorithms -- from linear regression to neural networks -- can have test performance that is non-monotonic in quantities such the sample size and model size. This striking phenomenon, often referred to as "double descent", has raised questions of if we need to re-think our current understanding of generalization. In this work, we study whether the double-descent phenomenon can be avoided by using optimal regularization. Theoretically, we prove that for certain linear regression models with isotropic data distribution, optimally-tuned $\ell_2$ regularization achieves monotonic test performance as we grow either the sample size or the model size. We also demonstrate empirically that optimally-tuned $\ell_2$ regularization can mitigate double descent for more general models, including neural networks. Our results suggest that it may also be informative to study the test risk scalings of various algorithms in the context of appropriately tuned regularization.

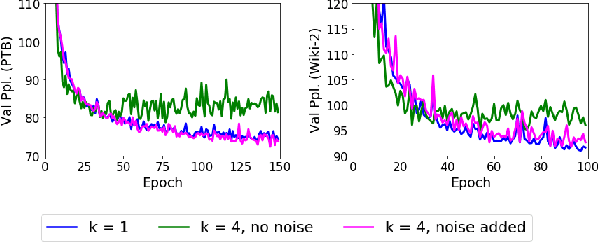
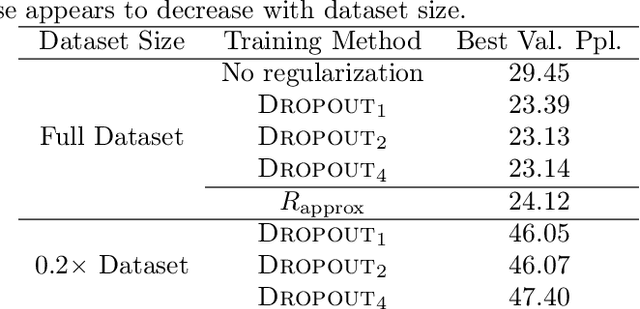
The Implicit and Explicit Regularization Effects of Dropout

Dropout is a widely-used regularization technique, often required to obtain state-of-the-art for a number of architectures. This work demonstrates that dropout introduces two distinct but entangled regularization effects: an explicit effect (also studied in prior work) which occurs since dropout modifies the expected training objective, and, perhaps surprisingly, an additional implicit effect from the stochasticity in the dropout training update. This implicit regularization effect is analogous to the effect of stochasticity in small mini-batch stochastic gradient descent. We disentangle these two effects through controlled experiments. We then derive analytic simplifications which characterize each effect in terms of the derivatives of the model and the loss, for deep neural networks. We demonstrate these simplified, analytic regularizers accurately capture the important aspects of dropout, showing they faithfully replace dropout in practice.