Segment Discovery: Enhancing E-commerce Targeting

Modern e-commerce services frequently target customers with incentives or interventions to engage them in their products such as games, shopping, video streaming, etc. This customer engagement increases acquisition of more customers and retention of existing ones, leading to more business for the company while improving customer experience. Often, customers are either randomly targeted or targeted based on the propensity of desirable behavior. However, such policies can be suboptimal as they do not target the set of customers who would benefit the most from the intervention and they may also not take account of any constraints. In this paper, we propose a policy framework based on uplift modeling and constrained optimization that identifies customers to target for a use-case specific intervention so as to maximize the value to the business, while taking account of any given constraints. We demonstrate improvement over state-of-the-art targeting approaches using two large-scale experimental studies and a production implementation.

Adaptive Experimentation When You Can't Experiment

This paper introduces the \emph{confounded pure exploration transductive linear bandit} (\texttt{CPET-LB}) problem. As a motivating example, often online services cannot directly assign users to specific control or treatment experiences either for business or practical reasons. In these settings, naively comparing treatment and control groups that may result from self-selection can lead to biased estimates of underlying treatment effects. Instead, online services can employ a properly randomized encouragement that incentivizes users toward a specific treatment. Our methodology provides online services with an adaptive experimental design approach for learning the best-performing treatment for such \textit{encouragement designs}. We consider a more general underlying model captured by a linear structural equation and formulate pure exploration linear bandits in this setting. Though pure exploration has been extensively studied in standard adaptive experimental design settings, we believe this is the first work considering a setting where noise is confounded. Elimination-style algorithms using experimental design methods in combination with a novel finite-time confidence interval on an instrumental variable style estimator are presented with sample complexity upper bounds nearly matching a minimax lower bound. Finally, experiments are conducted that demonstrate the efficacy of our approach.

Best of Three Worlds: Adaptive Experimentation for Digital Marketing in Practice

Adaptive experimental design (AED) methods are increasingly being used in industry as a tool to boost testing throughput or reduce experimentation cost relative to traditional A/B/N testing methods. However, the behavior and guarantees of such methods are not well-understood beyond idealized stationary settings. This paper shares lessons learned regarding the challenges of naively using AED systems in industrial settings where non-stationarity is prevalent, while also providing perspectives on the proper objectives and system specifications in such settings. We developed an AED framework for counterfactual inference based on these experiences, and tested it in a commercial environment.

Neural Insights for Digital Marketing Content Design

In digital marketing, experimenting with new website content is one of the key levers to improve customer engagement. However, creating successful marketing content is a manual and time-consuming process that lacks clear guiding principles. This paper seeks to close the loop between content creation and online experimentation by offering marketers AI-driven actionable insights based on historical data to improve their creative process. We present a neural-network-based system that scores and extracts insights from a marketing content design, namely, a multimodal neural network predicts the attractiveness of marketing contents, and a post-hoc attribution method generates actionable insights for marketers to improve their content in specific marketing locations. Our insights not only point out the advantages and drawbacks of a given current content, but also provide design recommendations based on historical data. We show that our scoring model and insights work well both quantitatively and qualitatively.

Adaptive Experimental Design and Counterfactual Inference

Adaptive experimental design methods are increasingly being used in industry as a tool to boost testing throughput or reduce experimentation cost relative to traditional A/B/N testing methods. This paper shares lessons learned regarding the challenges and pitfalls of naively using adaptive experimentation systems in industrial settings where non-stationarity is prevalent, while also providing perspectives on the proper objectives and system specifications in these settings. We developed an adaptive experimental design framework for counterfactual inference based on these experiences, and tested it in a commercial environment.

Online Learning in Periodic Zero-Sum Games

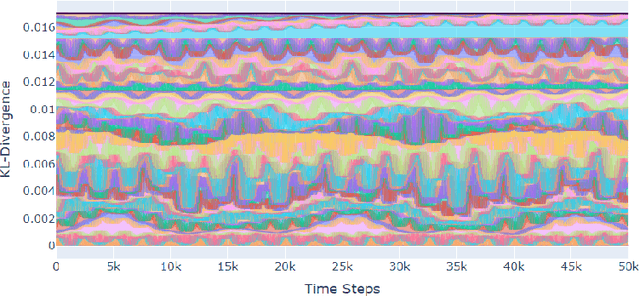
A seminal result in game theory is von Neumann's minmax theorem, which states that zero-sum games admit an essentially unique equilibrium solution. Classical learning results build on this theorem to show that online no-regret dynamics converge to an equilibrium in a time-average sense in zero-sum games. In the past several years, a key research direction has focused on characterizing the day-to-day behavior of such dynamics. General results in this direction show that broad classes of online learning dynamics are cyclic, and formally Poincar\'{e} recurrent, in zero-sum games. We analyze the robustness of these online learning behaviors in the case of periodic zero-sum games with a time-invariant equilibrium. This model generalizes the usual repeated game formulation while also being a realistic and natural model of a repeated competition between players that depends on exogenous environmental variations such as time-of-day effects, week-to-week trends, and seasonality. Interestingly, time-average convergence may fail even in the simplest such settings, in spite of the equilibrium being fixed. In contrast, using novel analysis methods, we show that Poincar\'{e} recurrence provably generalizes despite the complex, non-autonomous nature of these dynamical systems.

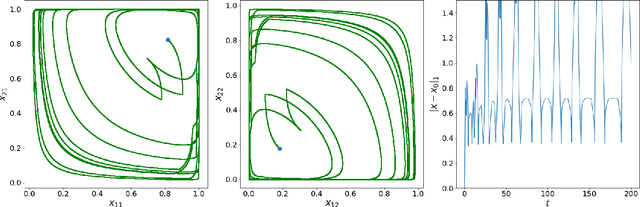
Stackelberg Actor-Critic: Game-Theoretic Reinforcement Learning Algorithms

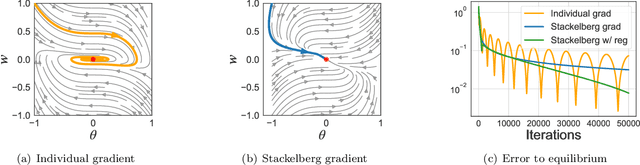
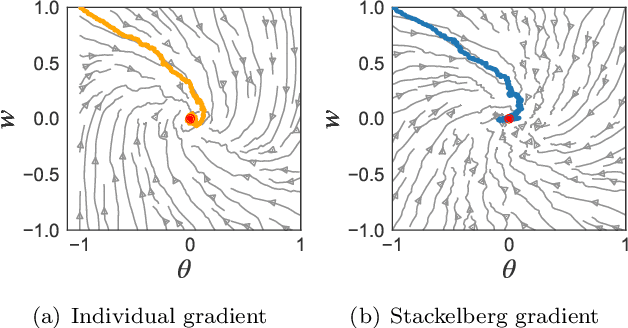
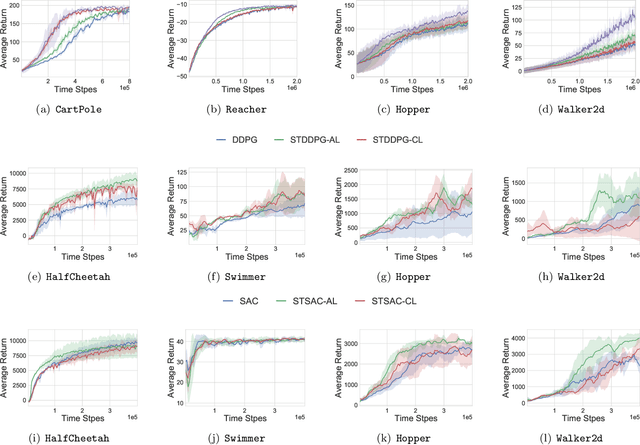
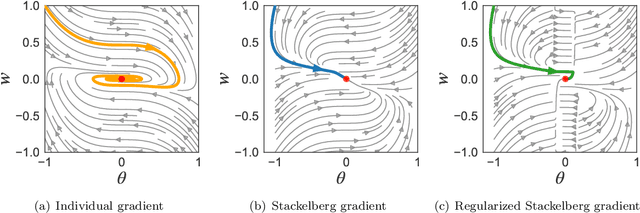
The hierarchical interaction between the actor and critic in actor-critic based reinforcement learning algorithms naturally lends itself to a game-theoretic interpretation. We adopt this viewpoint and model the actor and critic interaction as a two-player general-sum game with a leader-follower structure known as a Stackelberg game. Given this abstraction, we propose a meta-framework for Stackelberg actor-critic algorithms where the leader player follows the total derivative of its objective instead of the usual individual gradient. From a theoretical standpoint, we develop a policy gradient theorem for the refined update and provide a local convergence guarantee for the Stackelberg actor-critic algorithms to a local Stackelberg equilibrium. From an empirical standpoint, we demonstrate via simple examples that the learning dynamics we study mitigate cycling and accelerate convergence compared to the usual gradient dynamics given cost structures induced by actor-critic formulations. Finally, extensive experiments on OpenAI gym environments show that Stackelberg actor-critic algorithms always perform at least as well and often significantly outperform the standard actor-critic algorithm counterparts.

Minimax Optimization with Smooth Algorithmic Adversaries

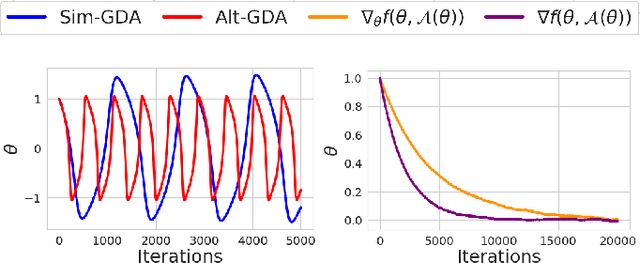
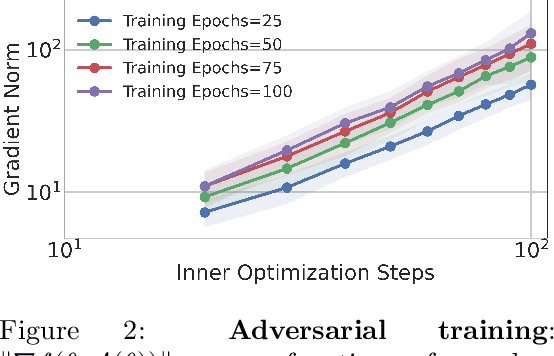
This paper considers minimax optimization $\min_x \max_y f(x, y)$ in the challenging setting where $f$ can be both nonconvex in $x$ and nonconcave in $y$. Though such optimization problems arise in many machine learning paradigms including training generative adversarial networks (GANs) and adversarially robust models, many fundamental issues remain in theory, such as the absence of efficiently computable optimality notions, and cyclic or diverging behavior of existing algorithms. Our framework sprouts from the practical consideration that under a computational budget, the max-player can not fully maximize $f(x,\cdot)$ since nonconcave maximization is NP-hard in general. So, we propose a new algorithm for the min-player to play against smooth algorithms deployed by the adversary (i.e., the max-player) instead of against full maximization. Our algorithm is guaranteed to make monotonic progress (thus having no limit cycles), and to find an appropriate "stationary point" in a polynomial number of iterations. Our framework covers practical settings where the smooth algorithms deployed by the adversary are multi-step stochastic gradient ascent, and its accelerated version. We further provide complementing experiments that confirm our theoretical findings and demonstrate the effectiveness of the proposed approach in practice.

Evolutionary Game Theory Squared: Evolving Agents in Endogenously Evolving Zero-Sum Games

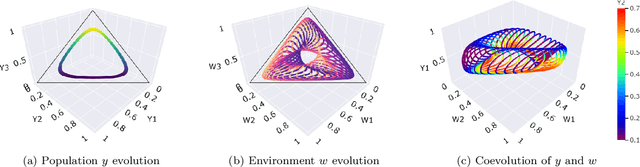
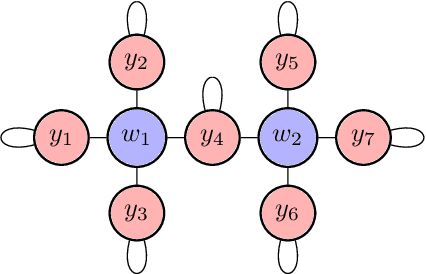
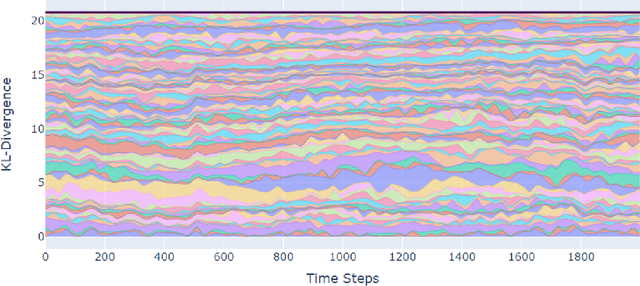
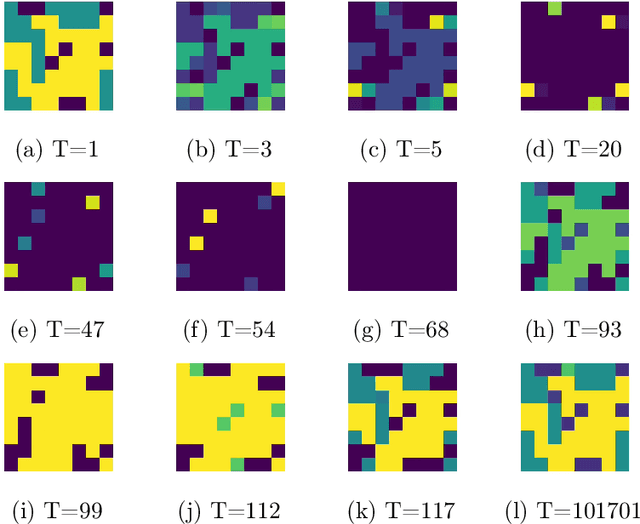
The predominant paradigm in evolutionary game theory and more generally online learning in games is based on a clear distinction between a population of dynamic agents that interact given a fixed, static game. In this paper, we move away from the artificial divide between dynamic agents and static games, to introduce and analyze a large class of competitive settings where both the agents and the games they play evolve strategically over time. We focus on arguably the most archetypal game-theoretic setting -- zero-sum games (as well as network generalizations) -- and the most studied evolutionary learning dynamic -- replicator, the continuous-time analogue of multiplicative weights. Populations of agents compete against each other in a zero-sum competition that itself evolves adversarially to the current population mixture. Remarkably, despite the chaotic coevolution of agents and games, we prove that the system exhibits a number of regularities. First, the system has conservation laws of an information-theoretic flavor that couple the behavior of all agents and games. Secondly, the system is Poincar\'{e} recurrent, with effectively all possible initializations of agents and games lying on recurrent orbits that come arbitrarily close to their initial conditions infinitely often. Thirdly, the time-average agent behavior and utility converge to the Nash equilibrium values of the time-average game. Finally, we provide a polynomial time algorithm to efficiently predict this time-average behavior for any such coevolving network game.

Gradient Descent-Ascent Provably Converges to Strict Local Minmax Equilibria with a Finite Timescale Separation

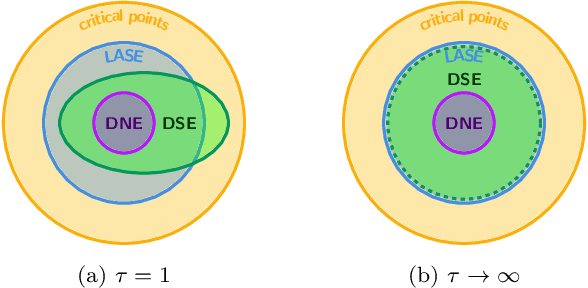
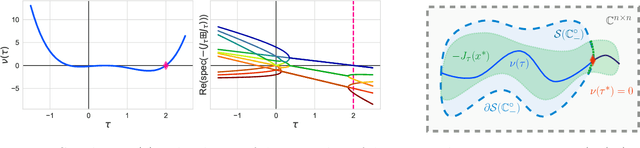
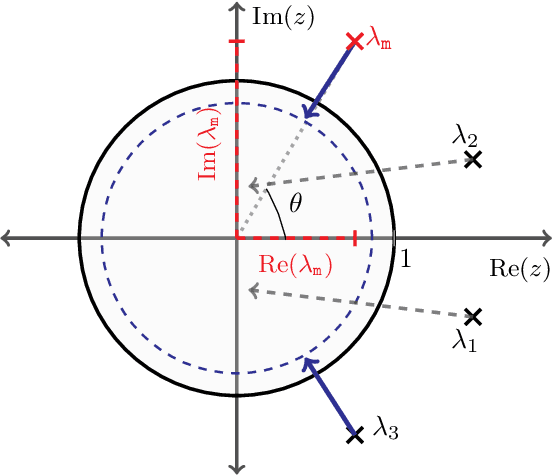
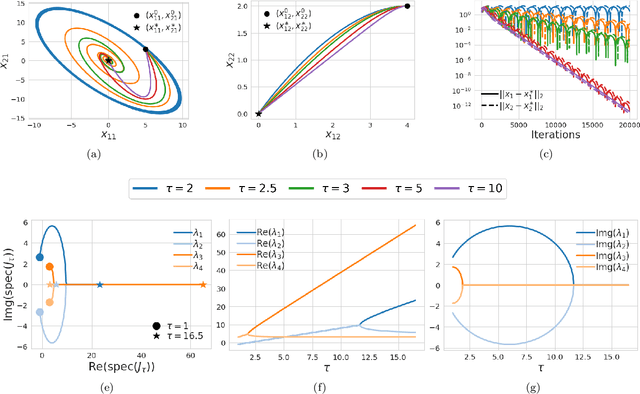
We study the role that a finite timescale separation parameter $\tau$ has on gradient descent-ascent in two-player non-convex, non-concave zero-sum games where the learning rate of player 1 is denoted by $\gamma_1$ and the learning rate of player 2 is defined to be $\gamma_2=\tau\gamma_1$. Existing work analyzing the role of timescale separation in gradient descent-ascent has primarily focused on the edge cases of players sharing a learning rate ($\tau =1$) and the maximizing player approximately converging between each update of the minimizing player ($\tau \rightarrow \infty$). For the parameter choice of $\tau=1$, it is known that the learning dynamics are not guaranteed to converge to a game-theoretically meaningful equilibria in general. In contrast, Jin et al. (2020) showed that the stable critical points of gradient descent-ascent coincide with the set of strict local minmax equilibria as $\tau\rightarrow\infty$. In this work, we bridge the gap between past work by showing there exists a finite timescale separation parameter $\tau^{\ast}$ such that $x^{\ast}$ is a stable critical point of gradient descent-ascent for all $\tau \in (\tau^{\ast}, \infty)$ if and only if it is a strict local minmax equilibrium. Moreover, we provide an explicit construction for computing $\tau^{\ast}$ along with corresponding convergence rates and results under deterministic and stochastic gradient feedback. The convergence results we present are complemented by a non-convergence result: given a critical point $x^{\ast}$ that is not a strict local minmax equilibrium, then there exists a finite timescale separation $\tau_0$ such that $x^{\ast}$ is unstable for all $\tau\in (\tau_0, \infty)$. Finally, we empirically demonstrate on the CIFAR-10 and CelebA datasets the significant impact timescale separation has on training performance.