Sample Complexity Reduction via Policy Difference Estimation in Tabular Reinforcement Learning

In this paper, we study the non-asymptotic sample complexity for the pure exploration problem in contextual bandits and tabular reinforcement learning (RL): identifying an epsilon-optimal policy from a set of policies with high probability. Existing work in bandits has shown that it is possible to identify the best policy by estimating only the difference between the behaviors of individual policies, which can be substantially cheaper than estimating the behavior of each policy directly. However, the best-known complexities in RL fail to take advantage of this and instead estimate the behavior of each policy directly. Does it suffice to estimate only the differences in the behaviors of policies in RL? We answer this question positively for contextual bandits but in the negative for tabular RL, showing a separation between contextual bandits and RL. However, inspired by this, we show that it almost suffices to estimate only the differences in RL: if we can estimate the behavior of a single reference policy, it suffices to only estimate how any other policy deviates from this reference policy. We develop an algorithm which instantiates this principle and obtains, to the best of our knowledge, the tightest known bound on the sample complexity of tabular RL.

Coupled Gradient Flows for Strategic Non-Local Distribution Shift

We propose a novel framework for analyzing the dynamics of distribution shift in real-world systems that captures the feedback loop between learning algorithms and the distributions on which they are deployed. Prior work largely models feedback-induced distribution shift as adversarial or via an overly simplistic distribution-shift structure. In contrast, we propose a coupled partial differential equation model that captures fine-grained changes in the distribution over time by accounting for complex dynamics that arise due to strategic responses to algorithmic decision-making, non-local endogenous population interactions, and other exogenous sources of distribution shift. We consider two common settings in machine learning: cooperative settings with information asymmetries, and competitive settings where a learner faces strategic users. For both of these settings, when the algorithm retrains via gradient descent, we prove asymptotic convergence of the retraining procedure to a steady-state, both in finite and in infinite dimensions, obtaining explicit rates in terms of the model parameters. To do so we derive new results on the convergence of coupled PDEs that extends what is known on multi-species systems. Empirically, we show that our approach captures well-documented forms of distribution shifts like polarization and disparate impacts that simpler models cannot capture.

Convergent First-Order Methods for Bi-level Optimization and Stackelberg Games

We propose an algorithm to solve a class of bi-level optimization problems using only first-order information. In particular, we focus on a class where the inner minimization has unique solutions. Unlike contemporary algorithms, our algorithm does not require the use of an oracle estimator for the gradient of the bi-level objective or an approximate solver for the inner problem. Instead, we alternate between descending on the inner problem using na\"ive optimization methods and descending on the upper-level objective function using specially constructed gradient estimators. We provide non-asymptotic convergence rates to stationary points of the bi-level objective in the absence of convexity of the closed-loop function and further show asymptotic convergence to only local minima of the bi-level problem. The approach is inspired by ideas from the literature on two-timescale stochastic approximation algorithms.

Fast Convergence of Optimistic Gradient Ascent in Network Zero-Sum Extensive Form Games

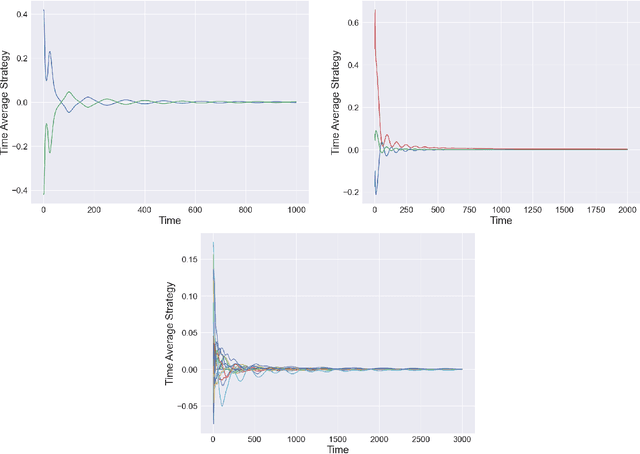
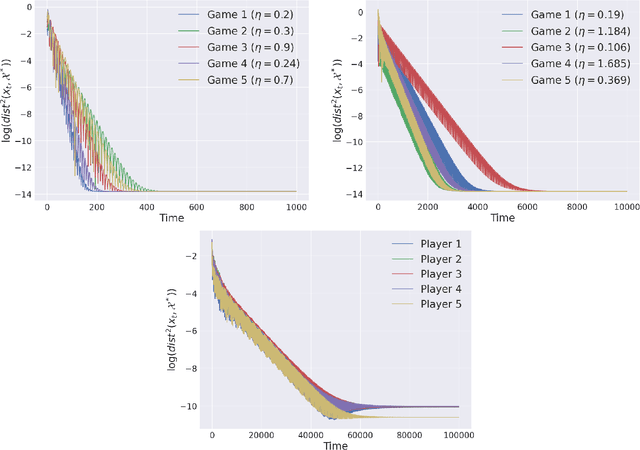
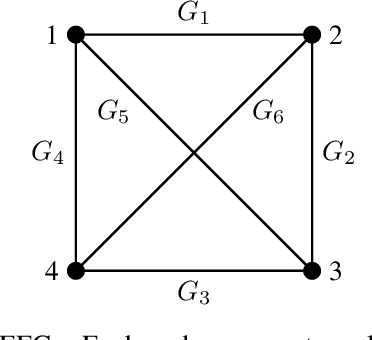
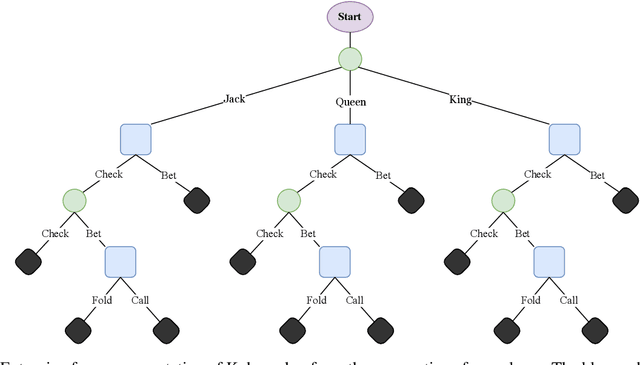
The study of learning in games has thus far focused primarily on normal form games. In contrast, our understanding of learning in extensive form games (EFGs) and particularly in EFGs with many agents lags far behind, despite them being closer in nature to many real world applications. We consider the natural class of Network Zero-Sum Extensive Form Games, which combines the global zero-sum property of agent payoffs, the efficient representation of graphical games as well the expressive power of EFGs. We examine the convergence properties of Optimistic Gradient Ascent (OGA) in these games. We prove that the time-average behavior of such online learning dynamics exhibits $O(1/T)$ rate convergence to the set of Nash Equilibria. Moreover, we show that the day-to-day behavior also converges to Nash with rate $O(c^{-t})$ for some game-dependent constant $c>0$.

Instance-optimal PAC Algorithms for Contextual Bandits

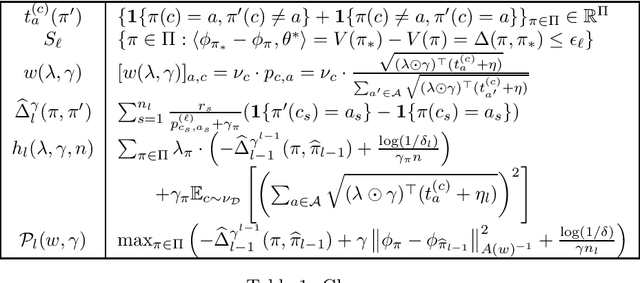
In the stochastic contextual bandit setting, regret-minimizing algorithms have been extensively researched, but their instance-minimizing best-arm identification counterparts remain seldom studied. In this work, we focus on the stochastic bandit problem in the $(\epsilon,\delta)$-$\textit{PAC}$ setting: given a policy class $\Pi$ the goal of the learner is to return a policy $\pi\in \Pi$ whose expected reward is within $\epsilon$ of the optimal policy with probability greater than $1-\delta$. We characterize the first $\textit{instance-dependent}$ PAC sample complexity of contextual bandits through a quantity $\rho_{\Pi}$, and provide matching upper and lower bounds in terms of $\rho_{\Pi}$ for the agnostic and linear contextual best-arm identification settings. We show that no algorithm can be simultaneously minimax-optimal for regret minimization and instance-dependent PAC for best-arm identification. Our main result is a new instance-optimal and computationally efficient algorithm that relies on a polynomial number of calls to an argmax oracle.

Online Learning in Periodic Zero-Sum Games

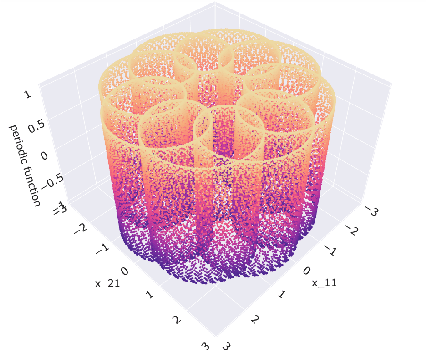
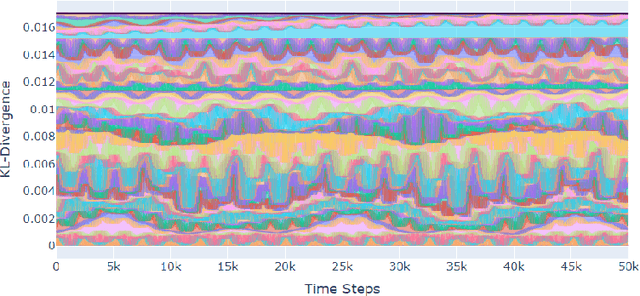
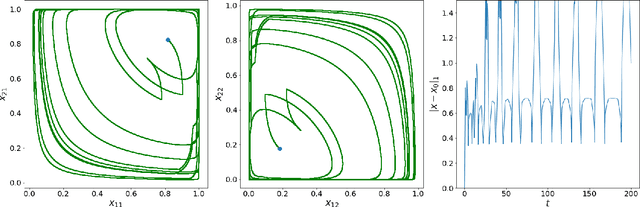
A seminal result in game theory is von Neumann's minmax theorem, which states that zero-sum games admit an essentially unique equilibrium solution. Classical learning results build on this theorem to show that online no-regret dynamics converge to an equilibrium in a time-average sense in zero-sum games. In the past several years, a key research direction has focused on characterizing the day-to-day behavior of such dynamics. General results in this direction show that broad classes of online learning dynamics are cyclic, and formally Poincar\'{e} recurrent, in zero-sum games. We analyze the robustness of these online learning behaviors in the case of periodic zero-sum games with a time-invariant equilibrium. This model generalizes the usual repeated game formulation while also being a realistic and natural model of a repeated competition between players that depends on exogenous environmental variations such as time-of-day effects, week-to-week trends, and seasonality. Interestingly, time-average convergence may fail even in the simplest such settings, in spite of the equilibrium being fixed. In contrast, using novel analysis methods, we show that Poincar\'{e} recurrence provably generalizes despite the complex, non-autonomous nature of these dynamical systems.

Evolutionary Game Theory Squared: Evolving Agents in Endogenously Evolving Zero-Sum Games

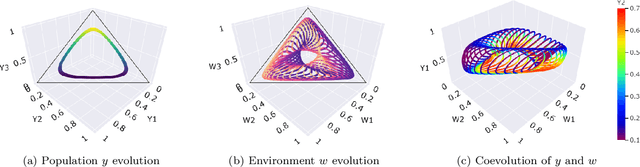
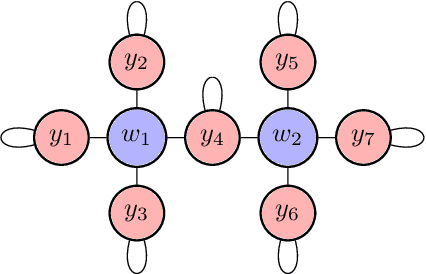
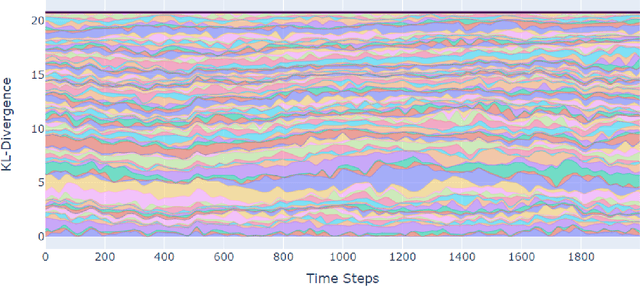
The predominant paradigm in evolutionary game theory and more generally online learning in games is based on a clear distinction between a population of dynamic agents that interact given a fixed, static game. In this paper, we move away from the artificial divide between dynamic agents and static games, to introduce and analyze a large class of competitive settings where both the agents and the games they play evolve strategically over time. We focus on arguably the most archetypal game-theoretic setting -- zero-sum games (as well as network generalizations) -- and the most studied evolutionary learning dynamic -- replicator, the continuous-time analogue of multiplicative weights. Populations of agents compete against each other in a zero-sum competition that itself evolves adversarially to the current population mixture. Remarkably, despite the chaotic coevolution of agents and games, we prove that the system exhibits a number of regularities. First, the system has conservation laws of an information-theoretic flavor that couple the behavior of all agents and games. Secondly, the system is Poincar\'{e} recurrent, with effectively all possible initializations of agents and games lying on recurrent orbits that come arbitrarily close to their initial conditions infinitely often. Thirdly, the time-average agent behavior and utility converge to the Nash equilibrium values of the time-average game. Finally, we provide a polynomial time algorithm to efficiently predict this time-average behavior for any such coevolving network game.

Gradient Descent-Ascent Provably Converges to Strict Local Minmax Equilibria with a Finite Timescale Separation

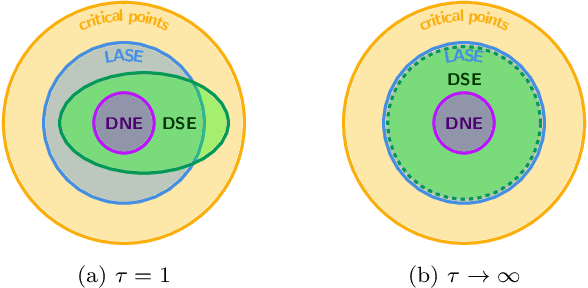
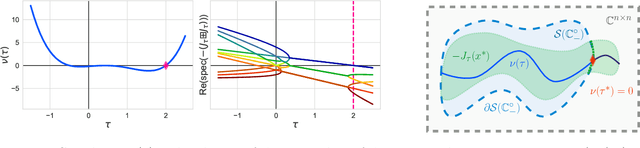
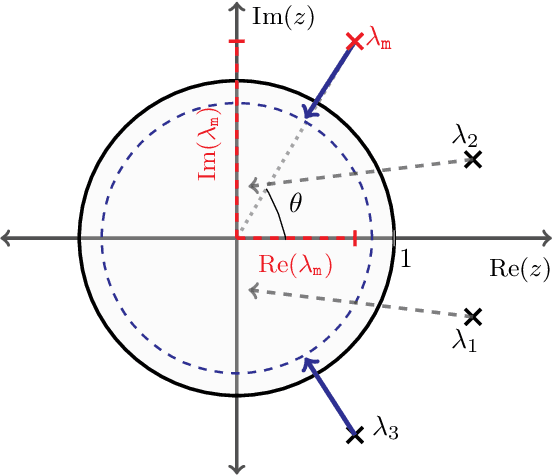
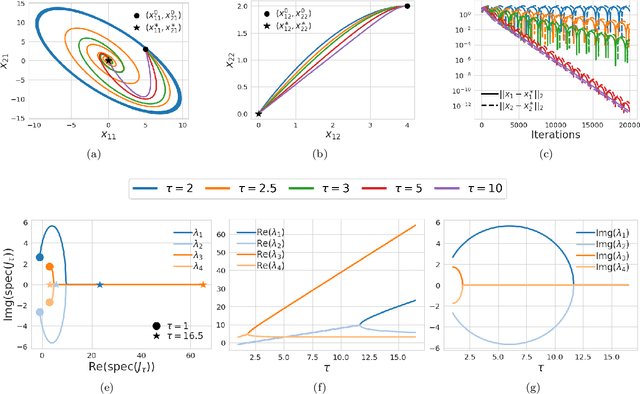
We study the role that a finite timescale separation parameter $\tau$ has on gradient descent-ascent in two-player non-convex, non-concave zero-sum games where the learning rate of player 1 is denoted by $\gamma_1$ and the learning rate of player 2 is defined to be $\gamma_2=\tau\gamma_1$. Existing work analyzing the role of timescale separation in gradient descent-ascent has primarily focused on the edge cases of players sharing a learning rate ($\tau =1$) and the maximizing player approximately converging between each update of the minimizing player ($\tau \rightarrow \infty$). For the parameter choice of $\tau=1$, it is known that the learning dynamics are not guaranteed to converge to a game-theoretically meaningful equilibria in general. In contrast, Jin et al. (2020) showed that the stable critical points of gradient descent-ascent coincide with the set of strict local minmax equilibria as $\tau\rightarrow\infty$. In this work, we bridge the gap between past work by showing there exists a finite timescale separation parameter $\tau^{\ast}$ such that $x^{\ast}$ is a stable critical point of gradient descent-ascent for all $\tau \in (\tau^{\ast}, \infty)$ if and only if it is a strict local minmax equilibrium. Moreover, we provide an explicit construction for computing $\tau^{\ast}$ along with corresponding convergence rates and results under deterministic and stochastic gradient feedback. The convergence results we present are complemented by a non-convergence result: given a critical point $x^{\ast}$ that is not a strict local minmax equilibrium, then there exists a finite timescale separation $\tau_0$ such that $x^{\ast}$ is unstable for all $\tau\in (\tau_0, \infty)$. Finally, we empirically demonstrate on the CIFAR-10 and CelebA datasets the significant impact timescale separation has on training performance.

A $\texttt{SUPER}^{\ast}$ Algorithm to Optimize Paper Bidding in Peer Review

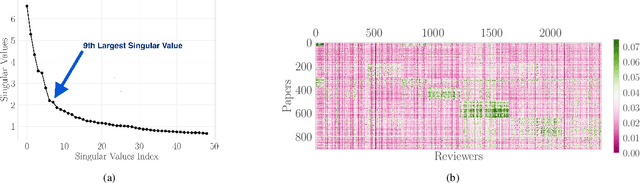
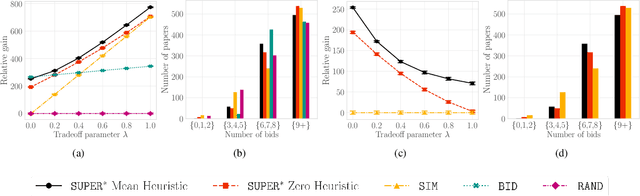
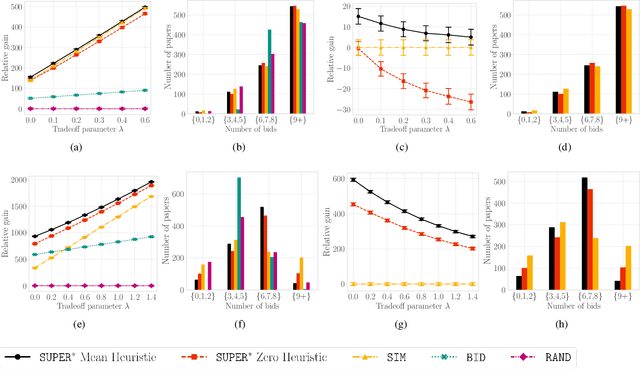
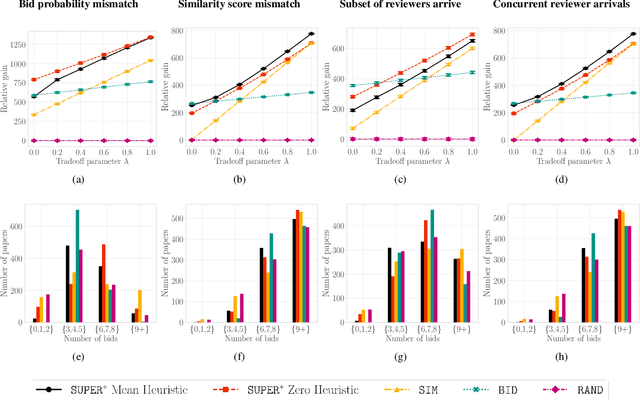
A number of applications involve sequential arrival of users, and require showing each user an ordering of items. A prime example (which forms the focus of this paper) is the bidding process in conference peer review where reviewers enter the system sequentially, each reviewer needs to be shown the list of submitted papers, and the reviewer then "bids" to review some papers. The order of the papers shown has a significant impact on the bids due to primacy effects. In deciding on the ordering of papers to show, there are two competing goals: (i) obtaining sufficiently many bids for each paper, and (ii) satisfying reviewers by showing them relevant items. In this paper, we begin by developing a framework to study this problem in a principled manner. We present an algorithm called $\texttt{SUPER}^{\ast}$, inspired by the A$^{\ast}$ algorithm, for this goal. Theoretically, we show a local optimality guarantee of our algorithm and prove that popular baselines are considerably suboptimal. Moreover, under a community model for the similarities, we prove that $\texttt{SUPER}^{\ast}$ is near-optimal whereas the popular baselines are considerably suboptimal. In experiments on real data from ICLR 2018 and synthetic data, we find that $\texttt{SUPER}^{\ast}$ considerably outperforms baselines deployed in existing systems, consistently reducing the number of papers with fewer than requisite bids by 50-75% or more, and is also robust to various real world complexities.

Sequential Experimental Design for Transductive Linear Bandits

In this paper we introduce the transductive linear bandit problem: given a set of measurement vectors $\mathcal{X}\subset \mathbb{R}^d$, a set of items $\mathcal{Z}\subset \mathbb{R}^d$, a fixed confidence $\delta$, and an unknown vector $\theta^{\ast}\in \mathbb{R}^d$, the goal is to infer $\text{argmax}_{z\in \mathcal{Z}} z^\top\theta^\ast$ with probability $1-\delta$ by making as few sequentially chosen noisy measurements of the form $x^\top\theta^{\ast}$ as possible. When $\mathcal{X}=\mathcal{Z}$, this setting generalizes linear bandits, and when $\mathcal{X}$ is the standard basis vectors and $\mathcal{Z}\subset \{0,1\}^d$, combinatorial bandits. Such a transductive setting naturally arises when the set of measurement vectors is limited due to factors such as availability or cost. As an example, in drug discovery the compounds and dosages $\mathcal{X}$ a practitioner may be willing to evaluate in the lab in vitro due to cost or safety reasons may differ vastly from those compounds and dosages $\mathcal{Z}$ that can be safely administered to patients in vivo. Alternatively, in recommender systems for books, the set of books $\mathcal{X}$ a user is queried about may be restricted to well known best-sellers even though the goal might be to recommend more esoteric titles $\mathcal{Z}$. In this paper, we provide instance-dependent lower bounds for the transductive setting, an algorithm that matches these up to logarithmic factors, and an evaluation. In particular, we provide the first non-asymptotic algorithm for linear bandits that nearly achieves the information theoretic lower bound.