Continuous-Time Analysis of Heavy Ball Momentum in Min-Max Games

Since Polyak's pioneering work, heavy ball (HB) momentum has been widely studied in minimization. However, its role in min-max games remains largely unexplored. As a key component of practical min-max algorithms like Adam, this gap limits their effectiveness. In this paper, we present a continuous-time analysis for HB with simultaneous and alternating update schemes in min-max games. Locally, we prove smaller momentum enhances algorithmic stability by enabling local convergence across a wider range of step sizes, with alternating updates generally converging faster. Globally, we study the implicit regularization of HB, and find smaller momentum guides algorithms trajectories towards shallower slope regions of the loss landscapes, with alternating updates amplifying this effect. Surprisingly, all these phenomena differ from those observed in minimization, where larger momentum yields similar effects. Our results reveal fundamental differences between HB in min-max games and minimization, and numerical experiments further validate our theoretical results.

Best of Both Worlds: Regret Minimization versus Minimax Play

In this paper, we investigate the existence of online learning algorithms with bandit feedback that simultaneously guarantee $O(1)$ regret compared to a given comparator strategy, and $O(\sqrt{T})$ regret compared to the best strategy in hindsight, where $T$ is the number of rounds. We provide the first affirmative answer to this question. In the context of symmetric zero-sum games, both in normal- and extensive form, we show that our results allow us to guarantee to risk at most $O(1)$ loss while being able to gain $\Omega(T)$ from exploitable opponents, thereby combining the benefits of both no-regret algorithms and minimax play.

Learning to Remove Cuts in Integer Linear Programming

Cutting plane methods are a fundamental approach for solving integer linear programs (ILPs). In each iteration of such methods, additional linear constraints (cuts) are introduced to the constraint set with the aim of excluding the previous fractional optimal solution while not affecting the optimal integer solution. In this work, we explore a novel approach within cutting plane methods: instead of only adding new cuts, we also consider the removal of previous cuts introduced at any of the preceding iterations of the method under a learnable parametric criteria. We demonstrate that in fundamental combinatorial optimization settings such cut removal policies can lead to significant improvements over both human-based and machine learning-guided cut addition policies even when implemented with simple models.

Efficient Continual Finite-Sum Minimization

Given a sequence of functions $f_1,\ldots,f_n$ with $f_i:\mathcal{D}\mapsto \mathbb{R}$, finite-sum minimization seeks a point ${x}^\star \in \mathcal{D}$ minimizing $\sum_{j=1}^n f_j(x)/n$. In this work, we propose a key twist into the finite-sum minimization, dubbed as continual finite-sum minimization, that asks for a sequence of points ${x}_1^\star,\ldots,{x}_n^\star \in \mathcal{D}$ such that each ${x}^\star_i \in \mathcal{D}$ minimizes the prefix-sum $\sum_{j=1}^if_j(x)/i$. Assuming that each prefix-sum is strongly convex, we develop a first-order continual stochastic variance reduction gradient method ($\mathrm{CSVRG}$) producing an $\epsilon$-optimal sequence with $\mathcal{\tilde{O}}(n/\epsilon^{1/3} + 1/\sqrt{\epsilon})$ overall first-order oracles (FO). An FO corresponds to the computation of a single gradient $\nabla f_j(x)$ at a given $x \in \mathcal{D}$ for some $j \in [n]$. Our approach significantly improves upon the $\mathcal{O}(n/\epsilon)$ FOs that $\mathrm{StochasticGradientDescent}$ requires and the $\mathcal{O}(n^2 \log (1/\epsilon))$ FOs that state-of-the-art variance reduction methods such as $\mathrm{Katyusha}$ require. We also prove that there is no natural first-order method with $\mathcal{O}\left(n/\epsilon^\alpha\right)$ gradient complexity for $\alpha < 1/4$, establishing that the first-order complexity of our method is nearly tight.

Imitation Learning in Discounted Linear MDPs without exploration assumptions

We present a new algorithm for imitation learning in infinite horizon linear MDPs dubbed ILARL which greatly improves the bound on the number of trajectories that the learner needs to sample from the environment. In particular, we remove exploration assumptions required in previous works and we improve the dependence on the desired accuracy $\epsilon$ from $\mathcal{O}\br{\epsilon^{-5}}$ to $\mathcal{O}\br{\epsilon^{-4}}$. Our result relies on a connection between imitation learning and online learning in MDPs with adversarial losses. For the latter setting, we present the first result for infinite horizon linear MDP which may be of independent interest. Moreover, we are able to provide a strengthen result for the finite horizon case where we achieve $\mathcal{O}\br{\epsilon^{-2}}$. Numerical experiments with linear function approximation shows that ILARL outperforms other commonly used algorithms.

Maximum Independent Set: Self-Training through Dynamic Programming

This work presents a graph neural network (GNN) framework for solving the maximum independent set (MIS) problem, inspired by dynamic programming (DP). Specifically, given a graph, we propose a DP-like recursive algorithm based on GNNs that firstly constructs two smaller sub-graphs, predicts the one with the larger MIS, and then uses it in the next recursive call. To train our algorithm, we require annotated comparisons of different graphs concerning their MIS size. Annotating the comparisons with the output of our algorithm leads to a self-training process that results in more accurate self-annotation of the comparisons and vice versa. We provide numerical evidence showing the superiority of our method vs prior methods in multiple synthetic and real-world datasets.

Min-Max Optimization Made Simple: Approximating the Proximal Point Method via Contraction Maps

In this paper we present a first-order method that admits near-optimal convergence rates for convex/concave min-max problems while requiring a simple and intuitive analysis. Similarly to the seminal work of Nemirovski and the recent approach of Piliouras et al. in normal form games, our work is based on the fact that the update rule of the Proximal Point method (PP) can be approximated up to accuracy $\epsilon$ with only $O(\log 1/\epsilon)$ additional gradient-calls through the iterations of a contraction map. Then combining the analysis of (PP) method with an error-propagation analysis we establish that the resulting first order method, called Clairvoyant Extra Gradient, admits near-optimal time-average convergence for general domains and last-iterate convergence in the unconstrained case.

Adaptive Stochastic Variance Reduction for Non-convex Finite-Sum Minimization

We propose an adaptive variance-reduction method, called AdaSpider, for minimization of $L$-smooth, non-convex functions with a finite-sum structure. In essence, AdaSpider combines an AdaGrad-inspired [Duchi et al., 2011, McMahan & Streeter, 2010], but a fairly distinct, adaptive step-size schedule with the recursive stochastic path integrated estimator proposed in [Fang et al., 2018]. To our knowledge, Adaspider is the first parameter-free non-convex variance-reduction method in the sense that it does not require the knowledge of problem-dependent parameters, such as smoothness constant $L$, target accuracy $\epsilon$ or any bound on gradient norms. In doing so, we are able to compute an $\epsilon$-stationary point with $\tilde{O}\left(n + \sqrt{n}/\epsilon^2\right)$ oracle-calls, which matches the respective lower bound up to logarithmic factors.

STay-ON-the-Ridge: Guaranteed Convergence to Local Minimax Equilibrium in Nonconvex-Nonconcave Games

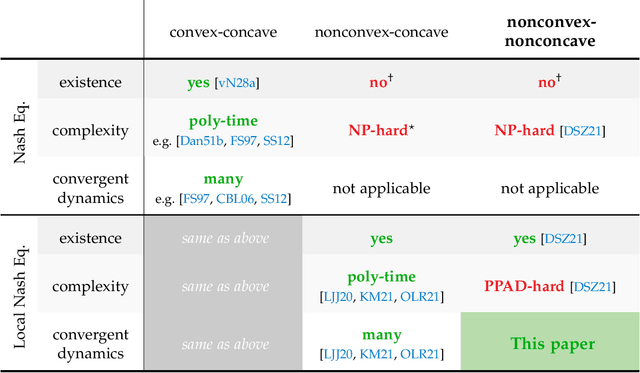
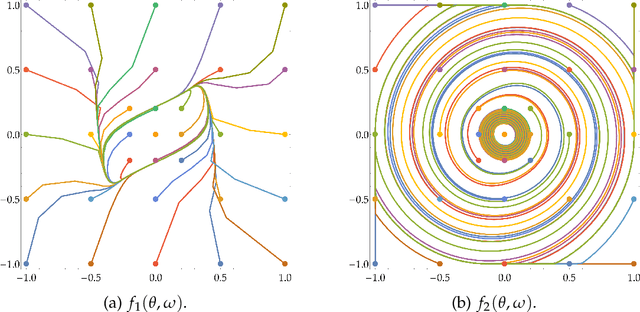
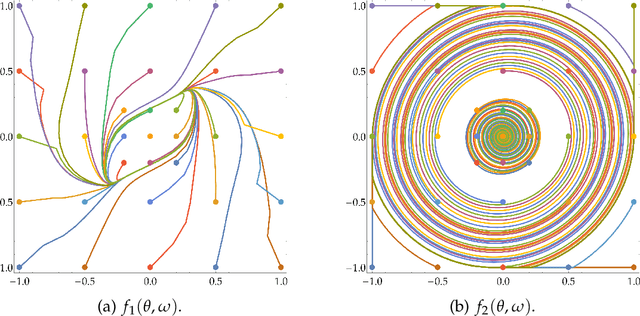
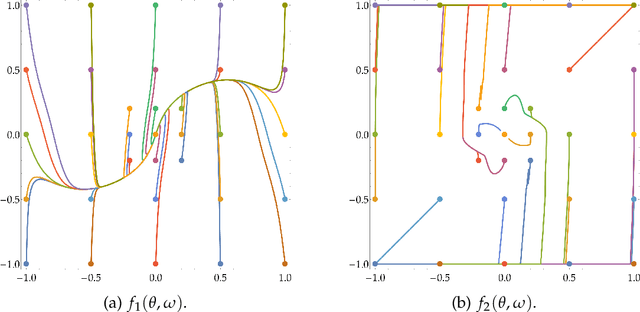
Min-max optimization problems involving nonconvex-nonconcave objectives have found important applications in adversarial training and other multi-agent learning settings. Yet, no known gradient descent-based method is guaranteed to converge to (even local notions of) min-max equilibrium in the nonconvex-nonconcave setting. For all known methods, there exist relatively simple objectives for which they cycle or exhibit other undesirable behavior different from converging to a point, let alone to some game-theoretically meaningful one~\cite{flokas2019poincare,hsieh2021limits}. The only known convergence guarantees hold under the strong assumption that the initialization is very close to a local min-max equilibrium~\cite{wang2019solving}. Moreover, the afore-described challenges are not just theoretical curiosities. All known methods are unstable in practice, even in simple settings. We propose the first method that is guaranteed to converge to a local min-max equilibrium for smooth nonconvex-nonconcave objectives. Our method is second-order and provably escapes limit cycles as long as it is initialized at an easy-to-find initial point. Both the definition of our method and its convergence analysis are motivated by the topological nature of the problem. In particular, our method is not designed to decrease some potential function, such as the distance of its iterate from the set of local min-max equilibria or the projected gradient of the objective, but is designed to satisfy a topological property that guarantees the avoidance of cycles and implies its convergence.

Fast Convergence of Optimistic Gradient Ascent in Network Zero-Sum Extensive Form Games

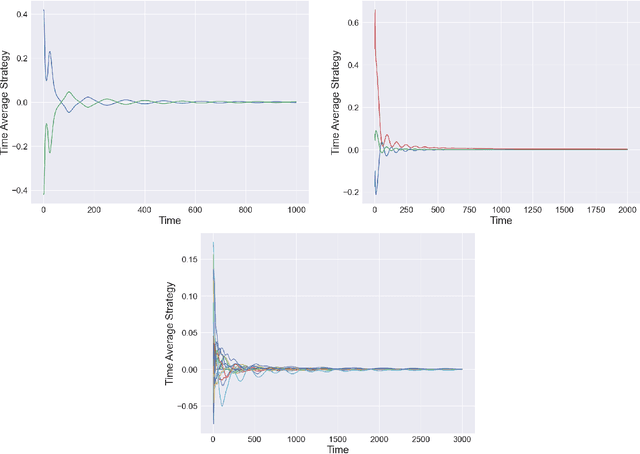
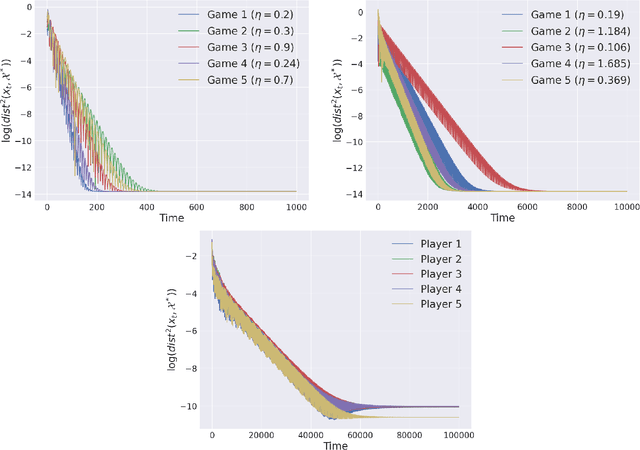
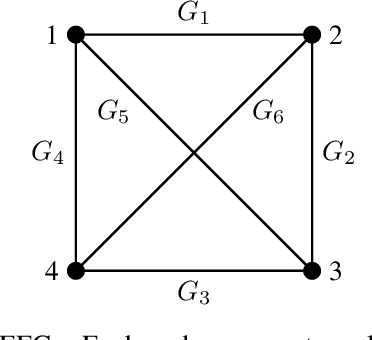
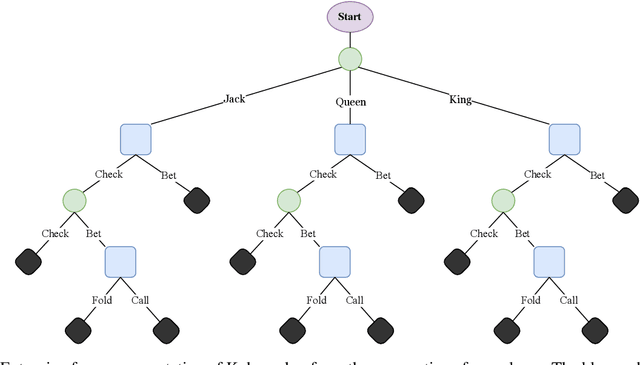
The study of learning in games has thus far focused primarily on normal form games. In contrast, our understanding of learning in extensive form games (EFGs) and particularly in EFGs with many agents lags far behind, despite them being closer in nature to many real world applications. We consider the natural class of Network Zero-Sum Extensive Form Games, which combines the global zero-sum property of agent payoffs, the efficient representation of graphical games as well the expressive power of EFGs. We examine the convergence properties of Optimistic Gradient Ascent (OGA) in these games. We prove that the time-average behavior of such online learning dynamics exhibits $O(1/T)$ rate convergence to the set of Nash Equilibria. Moreover, we show that the day-to-day behavior also converges to Nash with rate $O(c^{-t})$ for some game-dependent constant $c>0$.