Tolerant Algorithms for Learning with Arbitrary Covariate Shift

We study the problem of learning under arbitrary distribution shift, where the learner is trained on a labeled set from one distribution but evaluated on a different, potentially adversarially generated test distribution. We focus on two frameworks: PQ learning [Goldwasser, A. Kalai, Y. Kalai, Montasser NeurIPS 2020], allowing abstention on adversarially generated parts of the test distribution, and TDS learning [Klivans, Stavropoulos, Vasilyan COLT 2024], permitting abstention on the entire test distribution if distribution shift is detected. All prior known algorithms either rely on learning primitives that are computationally hard even for simple function classes, or end up abstaining entirely even in the presence of a tiny amount of distribution shift. We address both these challenges for natural function classes, including intersections of halfspaces and decision trees, and standard training distributions, including Gaussians. For PQ learning, we give efficient learning algorithms, while for TDS learning, our algorithms can tolerate moderate amounts of distribution shift. At the core of our approach is an improved analysis of spectral outlier-removal techniques from learning with nasty noise. Our analysis can (1) handle arbitrarily large fraction of outliers, which is crucial for handling arbitrary distribution shifts, and (2) obtain stronger bounds on polynomial moments of the distribution after outlier removal, yielding new insights into polynomial regression under distribution shifts. Lastly, our techniques lead to novel results for tolerant testable learning [Rubinfeld and Vasilyan STOC 2023], and learning with nasty noise.

Stochastic Bandits with ReLU Neural Networks

We study the stochastic bandit problem with ReLU neural network structure. We show that a $\tilde{O}(\sqrt{T})$ regret guarantee is achievable by considering bandits with one-layer ReLU neural networks; to the best of our knowledge, our work is the first to achieve such a guarantee. In this specific setting, we propose an OFU-ReLU algorithm that can achieve this upper bound. The algorithm first explores randomly until it reaches a linear regime, and then implements a UCB-type linear bandit algorithm to balance exploration and exploitation. Our key insight is that we can exploit the piecewise linear structure of ReLU activations and convert the problem into a linear bandit in a transformed feature space, once we learn the parameters of ReLU relatively accurately during the exploration stage. To remove dependence on model parameters, we design an OFU-ReLU+ algorithm based on a batching strategy, which can provide the same theoretical guarantee.

Complexity Matters: Dynamics of Feature Learning in the Presence of Spurious Correlations

Existing research often posits spurious features as "easier" to learn than core features in neural network optimization, but the impact of their relative simplicity remains under-explored. Moreover they mainly focus on the end performance intead of the learning dynamics of feature learning. In this paper, we propose a theoretical framework and associated synthetic dataset grounded in boolean function analysis which allows for fine-grained control on the relative complexity (compared to core features) and correlation strength (with respect to the label) of spurious features to study the dynamics of feature learning under spurious correlation. Our setup uncovers several interesting phenomenon: (1) stronger spurious correlations or simpler spurious features slow down the rate of learning for the core features, (2) learning phases of spurious features and core features are not always separable, (3) spurious features are not forgotten even after core features are fully learned. We show that our findings justify the success of retraining the last layer to remove spurious correlation and also identifies limitations of popular debiasing algorithms that exploit early learning of spurious features. We support our empirical findings with theoretical analyses for the case of learning XOR features with a one-hidden-layer ReLU network.

The Evolution of Statistical Induction Heads: In-Context Learning Markov Chains

Large language models have the ability to generate text that mimics patterns in their inputs. We introduce a simple Markov Chain sequence modeling task in order to study how this in-context learning (ICL) capability emerges. In our setting, each example is sampled from a Markov chain drawn from a prior distribution over Markov chains. Transformers trained on this task form \emph{statistical induction heads} which compute accurate next-token probabilities given the bigram statistics of the context. During the course of training, models pass through multiple phases: after an initial stage in which predictions are uniform, they learn to sub-optimally predict using in-context single-token statistics (unigrams); then, there is a rapid phase transition to the correct in-context bigram solution. We conduct an empirical and theoretical investigation of this multi-phase process, showing how successful learning results from the interaction between the transformer's layers, and uncovering evidence that the presence of the simpler unigram solution may delay formation of the final bigram solution. We examine how learning is affected by varying the prior distribution over Markov chains, and consider the generalization of our in-context learning of Markov chains (ICL-MC) task to $n$-grams for $n > 2$.

Pareto Frontiers in Neural Feature Learning: Data, Compute, Width, and Luck

This work investigates the nuanced algorithm design choices for deep learning in the presence of computational-statistical gaps. We begin by considering offline sparse parity learning, a supervised classification problem which admits a statistical query lower bound for gradient-based training of a multilayer perceptron. This lower bound can be interpreted as a multi-resource tradeoff frontier: successful learning can only occur if one is sufficiently rich (large model), knowledgeable (large dataset), patient (many training iterations), or lucky (many random guesses). We show, theoretically and experimentally, that sparse initialization and increasing network width yield significant improvements in sample efficiency in this setting. Here, width plays the role of parallel search: it amplifies the probability of finding "lottery ticket" neurons, which learn sparse features more sample-efficiently. Finally, we show that the synthetic sparse parity task can be useful as a proxy for real problems requiring axis-aligned feature learning. We demonstrate improved sample efficiency on tabular classification benchmarks by using wide, sparsely-initialized MLP models; these networks sometimes outperform tuned random forests.

Adversarial Resilience in Sequential Prediction via Abstention

We study the problem of sequential prediction in the stochastic setting with an adversary that is allowed to inject clean-label adversarial (or out-of-distribution) examples. Algorithms designed to handle purely stochastic data tend to fail in the presence of such adversarial examples, often leading to erroneous predictions. This is undesirable in many high-stakes applications such as medical recommendations, where abstaining from predictions on adversarial examples is preferable to misclassification. On the other hand, assuming fully adversarial data leads to very pessimistic bounds that are often vacuous in practice. To capture this motivation, we propose a new model of sequential prediction that sits between the purely stochastic and fully adversarial settings by allowing the learner to abstain from making a prediction at no cost on adversarial examples. Assuming access to the marginal distribution on the non-adversarial examples, we design a learner whose error scales with the VC dimension (mirroring the stochastic setting) of the hypothesis class, as opposed to the Littlestone dimension which characterizes the fully adversarial setting. Furthermore, we design a learner for VC dimension~1 classes, which works even in the absence of access to the marginal distribution. Our key technical contribution is a novel measure for quantifying uncertainty for learning VC classes, which may be of independent interest.

Exposing Attention Glitches with Flip-Flop Language Modeling

Why do large language models sometimes output factual inaccuracies and exhibit erroneous reasoning? The brittleness of these models, particularly when executing long chains of reasoning, currently seems to be an inevitable price to pay for their advanced capabilities of coherently synthesizing knowledge, pragmatics, and abstract thought. Towards making sense of this fundamentally unsolved problem, this work identifies and analyzes the phenomenon of attention glitches, in which the Transformer architecture's inductive biases intermittently fail to capture robust reasoning. To isolate the issue, we introduce flip-flop language modeling (FFLM), a parametric family of synthetic benchmarks designed to probe the extrapolative behavior of neural language models. This simple generative task requires a model to copy binary symbols over long-range dependencies, ignoring the tokens in between. We find that Transformer FFLMs suffer from a long tail of sporadic reasoning errors, some of which we can eliminate using various regularization techniques. Our preliminary mechanistic analyses show why the remaining errors may be very difficult to diagnose and resolve. We hypothesize that attention glitches account for (some of) the closed-domain hallucinations in natural LLMs.

Learning Narrow One-Hidden-Layer ReLU Networks

We consider the well-studied problem of learning a linear combination of $k$ ReLU activations with respect to a Gaussian distribution on inputs in $d$ dimensions. We give the first polynomial-time algorithm that succeeds whenever $k$ is a constant. All prior polynomial-time learners require additional assumptions on the network, such as positive combining coefficients or the matrix of hidden weight vectors being well-conditioned. Our approach is based on analyzing random contractions of higher-order moment tensors. We use a multi-scale analysis to argue that sufficiently close neurons can be collapsed together, sidestepping the conditioning issues present in prior work. This allows us to design an iterative procedure to discover individual neurons.

Transformers Learn Shortcuts to Automata

Algorithmic reasoning requires capabilities which are most naturally understood through recurrent models of computation, like the Turing machine. However, Transformer models, while lacking recurrence, are able to perform such reasoning using far fewer layers than the number of reasoning steps. This raises the question: what solutions are these shallow and non-recurrent models finding? We investigate this question in the setting of learning automata, discrete dynamical systems naturally suited to recurrent modeling and expressing algorithmic tasks. Our theoretical results completely characterize shortcut solutions, whereby a shallow Transformer with only $o(T)$ layers can exactly replicate the computation of an automaton on an input sequence of length $T$. By representing automata using the algebraic structure of their underlying transformation semigroups, we obtain $O(\log T)$-depth simulators for all automata and $O(1)$-depth simulators for all automata whose associated groups are solvable. Empirically, we perform synthetic experiments by training Transformers to simulate a wide variety of automata, and show that shortcut solutions can be learned via standard training. We further investigate the brittleness of these solutions and propose potential mitigations.

Recurrent Convolutional Neural Networks Learn Succinct Learning Algorithms

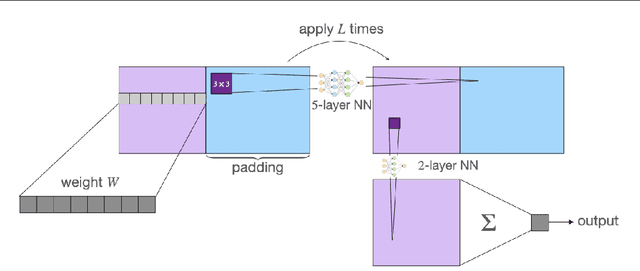
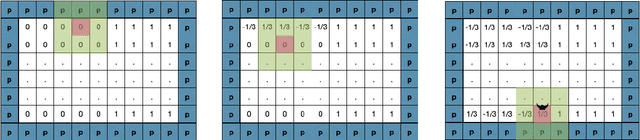
Neural Networks (NNs) struggle to efficiently learn certain problems, such as parity problems, even when there are simple learning algorithms for those problems. Can NNs discover learning algorithms on their own? We exhibit a NN architecture that, in polynomial time, learns as well as any efficient learning algorithm describable by a constant-sized learning algorithm. For example, on parity problems, the NN learns as well as row reduction, an efficient algorithm that can be succinctly described. Our architecture combines both recurrent weight-sharing between layers and convolutional weight-sharing to reduce the number of parameters down to a constant, even though the network itself may have trillions of nodes. While in practice the constants in our analysis are too large to be directly meaningful, our work suggests that the synergy of Recurrent and Convolutional NNs (RCNNs) may be more powerful than either alone.