Universal Rates of ERM for Agnostic Learning

The universal learning framework has been developed to obtain guarantees on the learning rates that hold for any fixed distribution, which can be much faster than the ones uniformly hold over all the distributions. Given that the Empirical Risk Minimization (ERM) principle being fundamental in the PAC theory and ubiquitous in practical machine learning, the recent work of arXiv:2412.02810 studied the universal rates of ERM for binary classification under the realizable setting. However, the assumption of realizability is too restrictive to hold in practice. Indeed, the majority of the literature on universal learning has focused on the realizable case, leaving the non-realizable case barely explored. In this paper, we consider the problem of universal learning by ERM for binary classification under the agnostic setting, where the ''learning curve" reflects the decay of the excess risk as the sample size increases. We explore the possibilities of agnostic universal rates and reveal a compact trichotomy: there are three possible agnostic universal rates of ERM, being either $e^{-n}$, $o(n^{-1/2})$, or arbitrarily slow. We provide a complete characterization of which concept classes fall into each of these categories. Moreover, we also establish complete characterizations for the target-dependent universal rates as well as the Bayes-dependent universal rates.

Private List Learnability vs. Online List Learnability

This work explores the connection between differential privacy (DP) and online learning in the context of PAC list learning. In this setting, a $k$-list learner outputs a list of $k$ potential predictions for an instance $x$ and incurs a loss if the true label of $x$ is not included in the list. A basic result in the multiclass PAC framework with a finite number of labels states that private learnability is equivalent to online learnability [Alon, Livni, Malliaris, and Moran (2019); Bun, Livni, and Moran (2020); Jung, Kim, and Tewari (2020)]. Perhaps surprisingly, we show that this equivalence does not hold in the context of list learning. Specifically, we prove that, unlike in the multiclass setting, a finite $k$-Littlestone dimensio--a variant of the classical Littlestone dimension that characterizes online $k$-list learnability--is not a sufficient condition for DP $k$-list learnability. However, similar to the multiclass case, we prove that it remains a necessary condition. To demonstrate where the equivalence breaks down, we provide an example showing that the class of monotone functions with $k+1$ labels over $\mathbb{N}$ is online $k$-list learnable, but not DP $k$-list learnable. This leads us to introduce a new combinatorial dimension, the \emph{$k$-monotone dimension}, which serves as a generalization of the threshold dimension. Unlike the multiclass setting, where the Littlestone and threshold dimensions are finite together, for $k>1$, the $k$-Littlestone and $k$-monotone dimensions do not exhibit this relationship. We prove that a finite $k$-monotone dimension is another necessary condition for DP $k$-list learnability, alongside finite $k$-Littlestone dimension. Whether the finiteness of both dimensions implies private $k$-list learnability remains an open question.

Data Selection for ERMs

Learning theory has traditionally followed a model-centric approach, focusing on designing optimal algorithms for a fixed natural learning task (e.g., linear classification or regression). In this paper, we adopt a complementary data-centric perspective, whereby we fix a natural learning rule and focus on optimizing the training data. Specifically, we study the following question: given a learning rule $\mathcal{A}$ and a data selection budget $n$, how well can $\mathcal{A}$ perform when trained on at most $n$ data points selected from a population of $N$ points? We investigate when it is possible to select $n \ll N$ points and achieve performance comparable to training on the entire population. We address this question across a variety of empirical risk minimizers. Our results include optimal data-selection bounds for mean estimation, linear classification, and linear regression. Additionally, we establish two general results: a taxonomy of error rates in binary classification and in stochastic convex optimization. Finally, we propose several open questions and directions for future research.

Proofs as Explanations: Short Certificates for Reliable Predictions

We consider a model for explainable AI in which an explanation for a prediction $h(x)=y$ consists of a subset $S'$ of the training data (if it exists) such that all classifiers $h' \in H$ that make at most $b$ mistakes on $S'$ predict $h'(x)=y$. Such a set $S'$ serves as a proof that $x$ indeed has label $y$ under the assumption that (1) the target function $h^\star$ belongs to $H$, and (2) the set $S$ contains at most $b$ corrupted points. For example, if $b=0$ and $H$ is the family of linear classifiers in $\mathbb{R}^d$, and if $x$ lies inside the convex hull of the positive data points in $S$ (and hence every consistent linear classifier labels $x$ as positive), then Carath\'eodory's theorem states that $x$ lies inside the convex hull of $d+1$ of those points. So, a set $S'$ of size $d+1$ could be released as an explanation for a positive prediction, and would serve as a short proof of correctness of the prediction under the assumption of realizability. In this work, we consider this problem more generally, for general hypothesis classes $H$ and general values $b\geq 0$. We define the notion of the robust hollow star number of $H$ (which generalizes the standard hollow star number), and show that it precisely characterizes the worst-case size of the smallest certificate achievable, and analyze its size for natural classes. We also consider worst-case distributional bounds on certificate size, as well as distribution-dependent bounds that we show tightly control the sample size needed to get a certificate for any given test example. In particular, we define a notion of the certificate coefficient $\varepsilon_x$ of an example $x$ with respect to a data distribution $D$ and target function $h^\star$, and prove matching upper and lower bounds on sample size as a function of $\varepsilon_x$, $b$, and the VC dimension $d$ of $H$.

A Theory of Optimistically Universal Online Learnability for General Concept Classes

We provide a full characterization of the concept classes that are optimistically universally online learnable with $\{0, 1\}$ labels. The notion of optimistically universal online learning was defined in [Hanneke, 2021] in order to understand learnability under minimal assumptions. In this paper, following the philosophy behind that work, we investigate two questions, namely, for every concept class: (1) What are the minimal assumptions on the data process admitting online learnability? (2) Is there a learning algorithm which succeeds under every data process satisfying the minimal assumptions? Such an algorithm is said to be optimistically universal for the given concept class. We resolve both of these questions for all concept classes, and moreover, as part of our solution, we design general learning algorithms for each case. Finally, we extend these algorithms and results to the agnostic case, showing an equivalence between the minimal assumptions on the data process for learnability in the agnostic and realizable cases, for every concept class, as well as the equivalence of optimistically universal learnability.

Learning from Snapshots of Discrete and Continuous Data Streams

Imagine a smart camera trap selectively clicking pictures to understand animal movement patterns within a particular habitat. These "snapshots", or pieces of data captured from a data stream at adaptively chosen times, provide a glimpse of different animal movements unfolding through time. Learning a continuous-time process through snapshots, such as smart camera traps, is a central theme governing a wide array of online learning situations. In this paper, we adopt a learning-theoretic perspective in understanding the fundamental nature of learning different classes of functions from both discrete data streams and continuous data streams. In our first framework, the \textit{update-and-deploy} setting, a learning algorithm discretely queries from a process to update a predictor designed to make predictions given as input the data stream. We construct a uniform sampling algorithm that can learn with bounded error any concept class with finite Littlestone dimension. Our second framework, known as the \emph{blind-prediction} setting, consists of a learning algorithm generating predictions independently of observing the process, only engaging with the process when it chooses to make queries. Interestingly, we show a stark contrast in learnability where non-trivial concept classes are unlearnable. However, we show that adaptive learning algorithms are necessary to learn sets of time-dependent and data-dependent functions, called pattern classes, in either framework. Finally, we develop a theory of pattern classes under discrete data streams for the blind-prediction setting.

Universal Rates of Empirical Risk Minimization

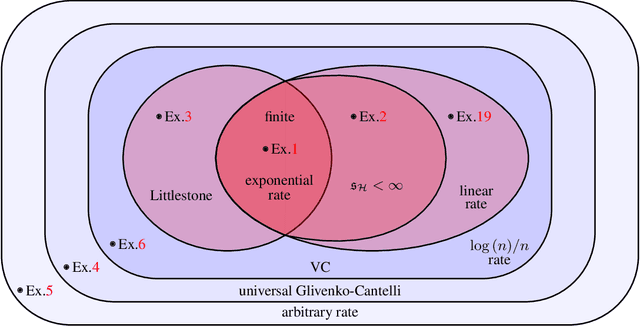
The well-known empirical risk minimization (ERM) principle is the basis of many widely used machine learning algorithms, and plays an essential role in the classical PAC theory. A common description of a learning algorithm's performance is its so-called "learning curve", that is, the decay of the expected error as a function of the input sample size. As the PAC model fails to explain the behavior of learning curves, recent research has explored an alternative universal learning model and has ultimately revealed a distinction between optimal universal and uniform learning rates (Bousquet et al., 2021). However, a basic understanding of such differences with a particular focus on the ERM principle has yet to be developed. In this paper, we consider the problem of universal learning by ERM in the realizable case and study the possible universal rates. Our main result is a fundamental tetrachotomy: there are only four possible universal learning rates by ERM, namely, the learning curves of any concept class learnable by ERM decay either at $e^{-n}$, $1/n$, $\log(n)/n$, or arbitrarily slow rates. Moreover, we provide a complete characterization of which concept classes fall into each of these categories, via new complexity structures. We also develop new combinatorial dimensions which supply sharp asymptotically-valid constant factors for these rates, whenever possible.

On the ERM Principle in Meta-Learning

Classic supervised learning involves algorithms trained on $n$ labeled examples to produce a hypothesis $h \in \mathcal{H}$ aimed at performing well on unseen examples. Meta-learning extends this by training across $n$ tasks, with $m$ examples per task, producing a hypothesis class $\mathcal{H}$ within some meta-class $\mathbb{H}$. This setting applies to many modern problems such as in-context learning, hypernetworks, and learning-to-learn. A common method for evaluating the performance of supervised learning algorithms is through their learning curve, which depicts the expected error as a function of the number of training examples. In meta-learning, the learning curve becomes a two-dimensional learning surface, which evaluates the expected error on unseen domains for varying values of $n$ (number of tasks) and $m$ (number of training examples). Our findings characterize the distribution-free learning surfaces of meta-Empirical Risk Minimizers when either $m$ or $n$ tend to infinity: we show that the number of tasks must increase inversely with the desired error. In contrast, we show that the number of examples exhibits very different behavior: it satisfies a dichotomy where every meta-class conforms to one of the following conditions: (i) either $m$ must grow inversely with the error, or (ii) a \emph{finite} number of examples per task suffices for the error to vanish as $n$ goes to infinity. This finding illustrates and characterizes cases in which a small number of examples per task is sufficient for successful learning. We further refine this for positive values of $\varepsilon$ and identify for each $\varepsilon$ how many examples per task are needed to achieve an error of $\varepsilon$ in the limit as the number of tasks $n$ goes to infinity. We achieve this by developing a necessary and sufficient condition for meta-learnability using a bounded number of examples per domain.

Multiclass Transductive Online Learning

We consider the problem of multiclass transductive online learning when the number of labels can be unbounded. Previous works by Ben-David et al. [1997] and Hanneke et al. [2023b] only consider the case of binary and finite label spaces, respectively. The latter work determined that their techniques fail to extend to the case of unbounded label spaces, and they pose the question of characterizing the optimal mistake bound for unbounded label spaces. We answer this question by showing that a new dimension, termed the Level-constrained Littlestone dimension, characterizes online learnability in this setting. Along the way, we show that the trichotomy of possible minimax rates of the expected number of mistakes established by Hanneke et al. [2023b] for finite label spaces in the realizable setting continues to hold even when the label space is unbounded. In particular, if the learner plays for $T \in \mathbb{N}$ rounds, its minimax expected number of mistakes can only grow like $\Theta(T)$, $\Theta(\log T)$, or $\Theta(1)$. To prove this result, we give another combinatorial dimension, termed the Level-constrained Branching dimension, and show that its finiteness characterizes constant minimax expected mistake-bounds. The trichotomy is then determined by a combination of the Level-constrained Littlestone and Branching dimensions. Quantitatively, our upper bounds improve upon existing multiclass upper bounds in Hanneke et al. [2023b] by removing the dependence on the label set size. In doing so, we explicitly construct learning algorithms that can handle extremely large or unbounded label spaces. A key and novel component of our algorithm is a new notion of shattering that exploits the sequential nature of transductive online learning. Finally, we complete our results by proving expected regret bounds in the agnostic setting, extending the result of Hanneke et al. [2023b].

Sample Compression Scheme Reductions

We present novel reductions from sample compression schemes in multiclass classification, regression, and adversarially robust learning settings to binary sample compression schemes. Assuming we have a compression scheme for binary classes of size $f(d_\mathrm{VC})$, where $d_\mathrm{VC}$ is the VC dimension, then we have the following results: (1) If the binary compression scheme is a majority-vote or a stable compression scheme, then there exists a multiclass compression scheme of size $O(f(d_\mathrm{G}))$, where $d_\mathrm{G}$ is the graph dimension. Moreover, for general binary compression schemes, we obtain a compression of size $O(f(d_\mathrm{G})\log|Y|)$, where $Y$ is the label space. (2) If the binary compression scheme is a majority-vote or a stable compression scheme, then there exists an $\epsilon$-approximate compression scheme for regression over $[0,1]$-valued functions of size $O(f(d_\mathrm{P}))$, where $d_\mathrm{P}$ is the pseudo-dimension. For general binary compression schemes, we obtain a compression of size $O(f(d_\mathrm{P})\log(1/\epsilon))$. These results would have significant implications if the sample compression conjecture, which posits that any binary concept class with a finite VC dimension admits a binary compression scheme of size $O(d_\mathrm{VC})$, is resolved (Littlestone and Warmuth, 1986; Floyd and Warmuth, 1995; Warmuth, 2003). Our results would then extend the proof of the conjecture immediately to other settings. We establish similar results for adversarially robust learning and also provide an example of a concept class that is robustly learnable but has no bounded-size compression scheme, demonstrating that learnability is not equivalent to having a compression scheme independent of the sample size, unlike in binary classification, where compression of size $2^{O(d_\mathrm{VC})}$ is attainable (Moran and Yehudayoff, 2016).