Sparse Linear Regression is Easy on Random Supports

Sparse linear regression is one of the most basic questions in machine learning and statistics. Here, we are given as input a design matrix $X \in \mathbb{R}^{N \times d}$ and measurements or labels ${y} \in \mathbb{R}^N$ where ${y} = {X} {w}^* + ξ$, and $ξ$ is the noise in the measurements. Importantly, we have the additional constraint that the unknown signal vector ${w}^*$ is sparse: it has $k$ non-zero entries where $k$ is much smaller than the ambient dimension. Our goal is to output a prediction vector $\widehat{w}$ that has small prediction error: $\frac{1}{N}\cdot \|{X} {w}^* - {X} \widehat{w}\|^2_2$. Information-theoretically, we know what is best possible in terms of measurements: under most natural noise distributions, we can get prediction error at most $ε$ with roughly $N = O(k \log d/ε)$ samples. Computationally, this currently needs $d^{Ω(k)}$ run-time. Alternately, with $N = O(d)$, we can get polynomial-time. Thus, there is an exponential gap (in the dependence on $d$) between the two and we do not know if it is possible to get $d^{o(k)}$ run-time and $o(d)$ samples. We give the first generic positive result for worst-case design matrices ${X}$: For any ${X}$, we show that if the support of ${w}^*$ is chosen at random, we can get prediction error $ε$ with $N = \text{poly}(k, \log d, 1/ε)$ samples and run-time $\text{poly}(d,N)$. This run-time holds for any design matrix ${X}$ with condition number up to $2^{\text{poly}(d)}$. Previously, such results were known for worst-case ${w}^*$, but only for random design matrices from well-behaved families, matrices that have a very low condition number ($\text{poly}(\log d)$; e.g., as studied in compressed sensing), or those with special structural properties.

Smoothed Analysis for Learning Concepts with Low Intrinsic Dimension

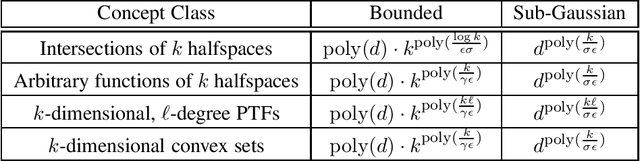
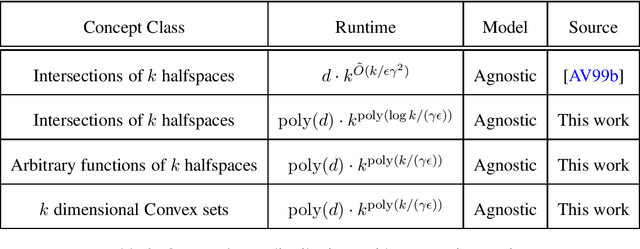
In traditional models of supervised learning, the goal of a learner -- given examples from an arbitrary joint distribution on $\mathbb{R}^d \times \{\pm 1\}$ -- is to output a hypothesis that is competitive (to within $\epsilon$) of the best fitting concept from some class. In order to escape strong hardness results for learning even simple concept classes, we introduce a smoothed-analysis framework that requires a learner to compete only with the best classifier that is robust to small random Gaussian perturbation. This subtle change allows us to give a wide array of learning results for any concept that (1) depends on a low-dimensional subspace (aka multi-index model) and (2) has a bounded Gaussian surface area. This class includes functions of halfspaces and (low-dimensional) convex sets, cases that are only known to be learnable in non-smoothed settings with respect to highly structured distributions such as Gaussians. Surprisingly, our analysis also yields new results for traditional non-smoothed frameworks such as learning with margin. In particular, we obtain the first algorithm for agnostically learning intersections of $k$-halfspaces in time $k^{poly(\frac{\log k}{\epsilon \gamma}) }$ where $\gamma$ is the margin parameter. Before our work, the best-known runtime was exponential in $k$ (Arriaga and Vempala, 1999).

On Convex Optimization with Semi-Sensitive Features

We study the differentially private (DP) empirical risk minimization (ERM) problem under the semi-sensitive DP setting where only some features are sensitive. This generalizes the Label DP setting where only the label is sensitive. We give improved upper and lower bounds on the excess risk for DP-ERM. In particular, we show that the error only scales polylogarithmically in terms of the sensitive domain size, improving upon previous results that scale polynomially in the sensitive domain size (Ghazi et al., 2021).

Learning Neural Networks with Sparse Activations

A core component present in many successful neural network architectures, is an MLP block of two fully connected layers with a non-linear activation in between. An intriguing phenomenon observed empirically, including in transformer architectures, is that, after training, the activations in the hidden layer of this MLP block tend to be extremely sparse on any given input. Unlike traditional forms of sparsity, where there are neurons/weights which can be deleted from the network, this form of {\em dynamic} activation sparsity appears to be harder to exploit to get more efficient networks. Motivated by this we initiate a formal study of PAC learnability of MLP layers that exhibit activation sparsity. We present a variety of results showing that such classes of functions do lead to provable computational and statistical advantages over their non-sparse counterparts. Our hope is that a better theoretical understanding of {\em sparsely activated} networks would lead to methods that can exploit activation sparsity in practice.

Lasso with Latents: Efficient Estimation, Covariate Rescaling, and Computational-Statistical Gaps

It is well-known that the statistical performance of Lasso can suffer significantly when the covariates of interest have strong correlations. In particular, the prediction error of Lasso becomes much worse than computationally inefficient alternatives like Best Subset Selection. Due to a large conjectured computational-statistical tradeoff in the problem of sparse linear regression, it may be impossible to close this gap in general. In this work, we propose a natural sparse linear regression setting where strong correlations between covariates arise from unobserved latent variables. In this setting, we analyze the problem caused by strong correlations and design a surprisingly simple fix. While Lasso with standard normalization of covariates fails, there exists a heterogeneous scaling of the covariates with which Lasso will suddenly obtain strong provable guarantees for estimation. Moreover, we design a simple, efficient procedure for computing such a "smart scaling." The sample complexity of the resulting "rescaled Lasso" algorithm incurs (in the worst case) quadratic dependence on the sparsity of the underlying signal. While this dependence is not information-theoretically necessary, we give evidence that it is optimal among the class of polynomial-time algorithms, via the method of low-degree polynomials. This argument reveals a new connection between sparse linear regression and a special version of sparse PCA with a near-critical negative spike. The latter problem can be thought of as a real-valued analogue of learning a sparse parity. Using it, we also establish the first computational-statistical gap for the closely related problem of learning a Gaussian Graphical Model.

Simple Mechanisms for Representing, Indexing and Manipulating Concepts

Deep networks typically learn concepts via classifiers, which involves setting up a model and training it via gradient descent to fit the concept-labeled data. We will argue instead that learning a concept could be done by looking at its moment statistics matrix to generate a concrete representation or signature of that concept. These signatures can be used to discover structure across the set of concepts and could recursively produce higher-level concepts by learning this structure from those signatures. When the concepts are `intersected', signatures of the concepts can be used to find a common theme across a number of related `intersected' concepts. This process could be used to keep a dictionary of concepts so that inputs could correctly identify and be routed to the set of concepts involved in the (latent) generation of the input.

User-Level Differential Privacy With Few Examples Per User

Previous work on user-level differential privacy (DP) [Ghazi et al. NeurIPS 2021, Bun et al. STOC 2023] obtained generic algorithms that work for various learning tasks. However, their focus was on the example-rich regime, where the users have so many examples that each user could themselves solve the problem. In this work we consider the example-scarce regime, where each user has only a few examples, and obtain the following results: 1. For approximate-DP, we give a generic transformation of any item-level DP algorithm to a user-level DP algorithm. Roughly speaking, the latter gives a (multiplicative) savings of $O_{\varepsilon,\delta}(\sqrt{m})$ in terms of the number of users required for achieving the same utility, where $m$ is the number of examples per user. This algorithm, while recovering most known bounds for specific problems, also gives new bounds, e.g., for PAC learning. 2. For pure-DP, we present a simple technique for adapting the exponential mechanism [McSherry, Talwar FOCS 2007] to the user-level setting. This gives new bounds for a variety of tasks, such as private PAC learning, hypothesis selection, and distribution learning. For some of these problems, we show that our bounds are near-optimal.

Feature Adaptation for Sparse Linear Regression

Sparse linear regression is a central problem in high-dimensional statistics. We study the correlated random design setting, where the covariates are drawn from a multivariate Gaussian $N(0,\Sigma)$, and we seek an estimator with small excess risk. If the true signal is $t$-sparse, information-theoretically, it is possible to achieve strong recovery guarantees with only $O(t\log n)$ samples. However, computationally efficient algorithms have sample complexity linear in (some variant of) the condition number of $\Sigma$. Classical algorithms such as the Lasso can require significantly more samples than necessary even if there is only a single sparse approximate dependency among the covariates. We provide a polynomial-time algorithm that, given $\Sigma$, automatically adapts the Lasso to tolerate a small number of approximate dependencies. In particular, we achieve near-optimal sample complexity for constant sparsity and if $\Sigma$ has few ``outlier'' eigenvalues. Our algorithm fits into a broader framework of feature adaptation for sparse linear regression with ill-conditioned covariates. With this framework, we additionally provide the first polynomial-factor improvement over brute-force search for constant sparsity $t$ and arbitrary covariance $\Sigma$.

On User-Level Private Convex Optimization

We introduce a new mechanism for stochastic convex optimization (SCO) with user-level differential privacy guarantees. The convergence rates of this mechanism are similar to those in the prior work of Levy et al. (2021); Narayanan et al. (2022), but with two important improvements. Our mechanism does not require any smoothness assumptions on the loss. Furthermore, our bounds are also the first where the minimum number of users needed for user-level privacy has no dependence on the dimension and only a logarithmic dependence on the desired excess error. The main idea underlying the new mechanism is to show that the optimizers of strongly convex losses have low local deletion sensitivity, along with an output perturbation method for functions with low local deletion sensitivity, which could be of independent interest.

Learning Narrow One-Hidden-Layer ReLU Networks

We consider the well-studied problem of learning a linear combination of $k$ ReLU activations with respect to a Gaussian distribution on inputs in $d$ dimensions. We give the first polynomial-time algorithm that succeeds whenever $k$ is a constant. All prior polynomial-time learners require additional assumptions on the network, such as positive combining coefficients or the matrix of hidden weight vectors being well-conditioned. Our approach is based on analyzing random contractions of higher-order moment tensors. We use a multi-scale analysis to argue that sufficiently close neurons can be collapsed together, sidestepping the conditioning issues present in prior work. This allows us to design an iterative procedure to discover individual neurons.