Everything Everywhere All at Once: LLMs can In-Context Learn Multiple Tasks in Superposition

Large Language Models (LLMs) have demonstrated remarkable in-context learning (ICL) capabilities. In this study, we explore a surprising phenomenon related to ICL: LLMs can perform multiple, computationally distinct ICL tasks simultaneously, during a single inference call, a capability we term "task superposition". We provide empirical evidence of this phenomenon across various LLM families and scales and show that this phenomenon emerges even if we train the model to in-context learn one task at a time. We offer theoretical explanations that this capability is well within the expressive power of transformers. We also explore how LLMs internally compose task vectors during superposition. Furthermore, we show that larger models can solve more ICL tasks in parallel, and better calibrate their output distribution. Our findings offer insights into the latent capabilities of LLMs, further substantiate the perspective of "LLMs as superposition of simulators", and raise questions about the mechanisms enabling simultaneous task execution.

PNeRV: A Polynomial Neural Representation for Videos

Extracting Implicit Neural Representations (INRs) on video data poses unique challenges due to the additional temporal dimension. In the context of videos, INRs have predominantly relied on a frame-only parameterization, which sacrifices the spatiotemporal continuity observed in pixel-level (spatial) representations. To mitigate this, we introduce Polynomial Neural Representation for Videos (PNeRV), a parameter-wise efficient, patch-wise INR for videos that preserves spatiotemporal continuity. PNeRV leverages the modeling capabilities of Polynomial Neural Networks to perform the modulation of a continuous spatial (patch) signal with a continuous time (frame) signal. We further propose a custom Hierarchical Patch-wise Spatial Sampling Scheme that ensures spatial continuity while retaining parameter efficiency. We also employ a carefully designed Positional Embedding methodology to further enhance PNeRV's performance. Our extensive experimentation demonstrates that PNeRV outperforms the baselines in conventional Implicit Neural Representation tasks like compression along with downstream applications that require spatiotemporal continuity in the underlying representation. PNeRV not only addresses the challenges posed by video data in the realm of INRs but also opens new avenues for advanced video processing and analysis.

Robust NAS under adversarial training: benchmark, theory, and beyond

Recent developments in neural architecture search (NAS) emphasize the significance of considering robust architectures against malicious data. However, there is a notable absence of benchmark evaluations and theoretical guarantees for searching these robust architectures, especially when adversarial training is considered. In this work, we aim to address these two challenges, making twofold contributions. First, we release a comprehensive data set that encompasses both clean accuracy and robust accuracy for a vast array of adversarially trained networks from the NAS-Bench-201 search space on image datasets. Then, leveraging the neural tangent kernel (NTK) tool from deep learning theory, we establish a generalization theory for searching architecture in terms of clean accuracy and robust accuracy under multi-objective adversarial training. We firmly believe that our benchmark and theoretical insights will significantly benefit the NAS community through reliable reproducibility, efficient assessment, and theoretical foundation, particularly in the pursuit of robust architectures.

On the Convergence of Encoder-only Shallow Transformers

In this paper, we aim to build the global convergence theory of encoder-only shallow Transformers under a realistic setting from the perspective of architectures, initialization, and scaling under a finite width regime. The difficulty lies in how to tackle the softmax in self-attention mechanism, the core ingredient of Transformer. In particular, we diagnose the scaling scheme, carefully tackle the input/output of softmax, and prove that quadratic overparameterization is sufficient for global convergence of our shallow Transformers under commonly-used He/LeCun initialization in practice. Besides, neural tangent kernel (NTK) based analysis is also given, which facilitates a comprehensive comparison. Our theory demonstrates the separation on the importance of different scaling schemes and initialization. We believe our results can pave the way for a better understanding of modern Transformers, particularly on training dynamics.

Maximum Independent Set: Self-Training through Dynamic Programming

This work presents a graph neural network (GNN) framework for solving the maximum independent set (MIS) problem, inspired by dynamic programming (DP). Specifically, given a graph, we propose a DP-like recursive algorithm based on GNNs that firstly constructs two smaller sub-graphs, predicts the one with the larger MIS, and then uses it in the next recursive call. To train our algorithm, we require annotated comparisons of different graphs concerning their MIS size. Annotating the comparisons with the output of our algorithm leads to a self-training process that results in more accurate self-annotation of the comparisons and vice versa. We provide numerical evidence showing the superiority of our method vs prior methods in multiple synthetic and real-world datasets.

Benign Overfitting in Deep Neural Networks under Lazy Training

This paper focuses on over-parameterized deep neural networks (DNNs) with ReLU activation functions and proves that when the data distribution is well-separated, DNNs can achieve Bayes-optimal test error for classification while obtaining (nearly) zero-training error under the lazy training regime. For this purpose, we unify three interrelated concepts of overparameterization, benign overfitting, and the Lipschitz constant of DNNs. Our results indicate that interpolating with smoother functions leads to better generalization. Furthermore, we investigate the special case where interpolating smooth ground-truth functions is performed by DNNs under the Neural Tangent Kernel (NTK) regime for generalization. Our result demonstrates that the generalization error converges to a constant order that only depends on label noise and initialization noise, which theoretically verifies benign overfitting. Our analysis provides a tight lower bound on the normalized margin under non-smooth activation functions, as well as the minimum eigenvalue of NTK under high-dimensional settings, which has its own interest in learning theory.

Regularization of polynomial networks for image recognition

Deep Neural Networks (DNNs) have obtained impressive performance across tasks, however they still remain as black boxes, e.g., hard to theoretically analyze. At the same time, Polynomial Networks (PNs) have emerged as an alternative method with a promising performance and improved interpretability but have yet to reach the performance of the powerful DNN baselines. In this work, we aim to close this performance gap. We introduce a class of PNs, which are able to reach the performance of ResNet across a range of six benchmarks. We demonstrate that strong regularization is critical and conduct an extensive study of the exact regularization schemes required to match performance. To further motivate the regularization schemes, we introduce D-PolyNets that achieve a higher-degree of expansion than previously proposed polynomial networks. D-PolyNets are more parameter-efficient while achieving a similar performance as other polynomial networks. We expect that our new models can lead to an understanding of the role of elementwise activation functions (which are no longer required for training PNs). The source code is available at https://github.com/grigorisg9gr/regularized_polynomials.

Extrapolation and Spectral Bias of Neural Nets with Hadamard Product: a Polynomial Net Study

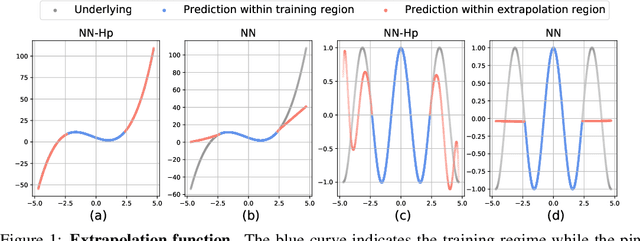
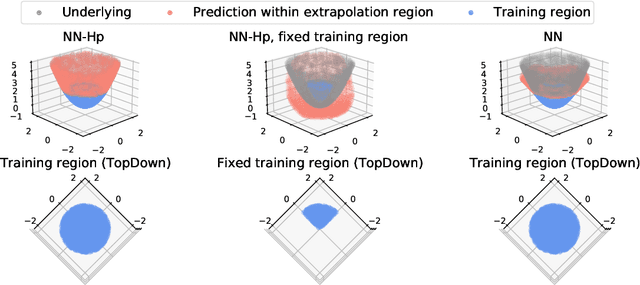
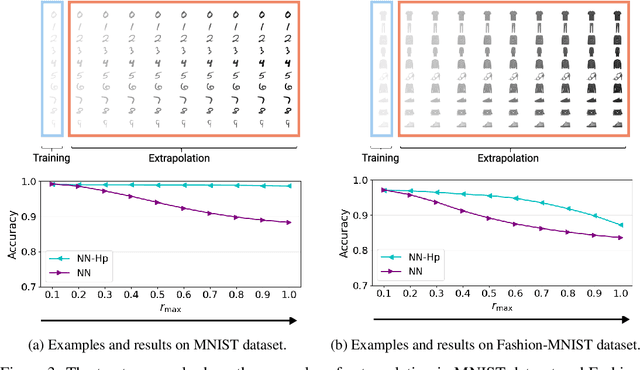
Neural tangent kernel (NTK) is a powerful tool to analyze training dynamics of neural networks and their generalization bounds. The study on NTK has been devoted to typical neural network architectures, but is incomplete for neural networks with Hadamard products (NNs-Hp), e.g., StyleGAN and polynomial neural networks. In this work, we derive the finite-width NTK formulation for a special class of NNs-Hp, i.e., polynomial neural networks. We prove their equivalence to the kernel regression predictor with the associated NTK, which expands the application scope of NTK. Based on our results, we elucidate the separation of PNNs over standard neural networks with respect to extrapolation and spectral bias. Our two key insights are that when compared to standard neural networks, PNNs are able to fit more complicated functions in the extrapolation regime and admit a slower eigenvalue decay of the respective NTK. Besides, our theoretical results can be extended to other types of NNs-Hp, which expand the scope of our work. Our empirical results validate the separations in broader classes of NNs-Hp, which provide a good justification for a deeper understanding of neural architectures.

Robustness in deep learning: The good , the bad , and the ugly

We study the average robustness notion in deep neural networks in (selected) wide and narrow, deep and shallow, as well as lazy and non-lazy training settings. We prove that in the under-parameterized setting, width has a negative effect while it improves robustness in the over-parameterized setting. The effect of depth closely depends on the initialization and the training mode. In particular, when initialized with LeCun initialization, depth helps robustness with lazy training regime. In contrast, when initialized with Neural Tangent Kernel (NTK) and He-initialization, depth hurts the robustness. Moreover, under non-lazy training regime, we demonstrate how the width of a two-layer ReLU network benefits robustness. Our theoretical developments improve the results by Huang et al. [2021], Wu et al. [2021] and are consistent with Bubeck and Sellke [2021], Bubeck et al. [2021].

Generalization Properties of NAS under Activation and Skip Connection Search

Neural Architecture Search (NAS) has fostered the automatic discovery of neural architectures, which achieve state-of-the-art accuracy in image recognition. Despite the progress achieved with NAS, so far there is little attention to theoretical guarantees on NAS. In this work, we study the generalization properties of NAS under a unifying framework enabling (deep) layer skip connection search and activation function search. To this end, we derive the lower (and upper) bounds of the minimum eigenvalue of Neural Tangent Kernel under the (in)finite width regime from a search space including mixed activation functions, fully connected, and residual neural networks. Our analysis is non-trivial due to the coupling of various architectures and activation functions under the unifying framework. Then, we leverage the eigenvalue bounds to establish generalization error bounds of NAS in the stochastic gradient descent training. Importantly, we theoretically and experimentally show how the derived results can guide NAS to select the top-performing architectures, even in the case without training, leading to a training-free algorithm based on our theory. Accordingly, our numerical validation shed light on the design of computationally efficient methods for NAS.