Adaptive and Optimal Second-order Optimistic Methods for Minimax Optimization

We propose adaptive, line search-free second-order methods with optimal rate of convergence for solving convex-concave min-max problems. By means of an adaptive step size, our algorithms feature a simple update rule that requires solving only one linear system per iteration, eliminating the need for line search or backtracking mechanisms. Specifically, we base our algorithms on the optimistic method and appropriately combine it with second-order information. Moreover, distinct from common adaptive schemes, we define the step size recursively as a function of the gradient norm and the prediction error in the optimistic update. We first analyze a variant where the step size requires knowledge of the Lipschitz constant of the Hessian. Under the additional assumption of Lipschitz continuous gradients, we further design a parameter-free version by tracking the Hessian Lipschitz constant locally and ensuring the iterates remain bounded. We also evaluate the practical performance of our algorithm by comparing it to existing second-order algorithms for minimax optimization.

Adaptive Stochastic Variance Reduction for Non-convex Finite-Sum Minimization

We propose an adaptive variance-reduction method, called AdaSpider, for minimization of $L$-smooth, non-convex functions with a finite-sum structure. In essence, AdaSpider combines an AdaGrad-inspired [Duchi et al., 2011, McMahan & Streeter, 2010], but a fairly distinct, adaptive step-size schedule with the recursive stochastic path integrated estimator proposed in [Fang et al., 2018]. To our knowledge, Adaspider is the first parameter-free non-convex variance-reduction method in the sense that it does not require the knowledge of problem-dependent parameters, such as smoothness constant $L$, target accuracy $\epsilon$ or any bound on gradient norms. In doing so, we are able to compute an $\epsilon$-stationary point with $\tilde{O}\left(n + \sqrt{n}/\epsilon^2\right)$ oracle-calls, which matches the respective lower bound up to logarithmic factors.

Extra-Newton: A First Approach to Noise-Adaptive Accelerated Second-Order Methods

This work proposes a universal and adaptive second-order method for minimizing second-order smooth, convex functions. Our algorithm achieves $O(\sigma / \sqrt{T})$ convergence when the oracle feedback is stochastic with variance $\sigma^2$, and improves its convergence to $O( 1 / T^3)$ with deterministic oracles, where $T$ is the number of iterations. Our method also interpolates these rates without knowing the nature of the oracle apriori, which is enabled by a parameter-free adaptive step-size that is oblivious to the knowledge of smoothness modulus, variance bounds and the diameter of the constrained set. To our knowledge, this is the first universal algorithm with such global guarantees within the second-order optimization literature.

High Probability Bounds for a Class of Nonconvex Algorithms with AdaGrad Stepsize

In this paper, we propose a new, simplified high probability analysis of AdaGrad for smooth, non-convex problems. More specifically, we focus on a particular accelerated gradient (AGD) template (Lan, 2020), through which we recover the original AdaGrad and its variant with averaging, and prove a convergence rate of $\mathcal O (1/ \sqrt{T})$ with high probability without the knowledge of smoothness and variance. We use a particular version of Freedman's concentration bound for martingale difference sequences (Kakade & Tewari, 2008) which enables us to achieve the best-known dependence of $\log (1 / \delta )$ on the probability margin $\delta$. We present our analysis in a modular way and obtain a complementary $\mathcal O (1 / T)$ convergence rate in the deterministic setting. To the best of our knowledge, this is the first high probability result for AdaGrad with a truly adaptive scheme, i.e., completely oblivious to the knowledge of smoothness and uniform variance bound, which simultaneously has best-known dependence of $\log( 1/ \delta)$. We further prove noise adaptation property of AdaGrad under additional noise assumptions.

STORM+: Fully Adaptive SGD with Momentum for Nonconvex Optimization

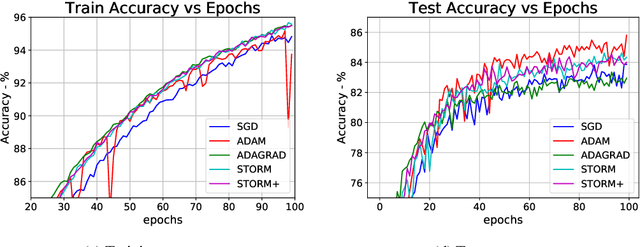
In this work we investigate stochastic non-convex optimization problems where the objective is an expectation over smooth loss functions, and the goal is to find an approximate stationary point. The most popular approach to handling such problems is variance reduction techniques, which are also known to obtain tight convergence rates, matching the lower bounds in this case. Nevertheless, these techniques require a careful maintenance of anchor points in conjunction with appropriately selected "mega-batchsizes". This leads to a challenging hyperparameter tuning problem, that weakens their practicality. Recently, [Cutkosky and Orabona, 2019] have shown that one can employ recursive momentum in order to avoid the use of anchor points and large batchsizes, and still obtain the optimal rate for this setting. Yet, their method called STORM crucially relies on the knowledge of the smoothness, as well a bound on the gradient norms. In this work we propose STORM+, a new method that is completely parameter-free, does not require large batch-sizes, and obtains the optimal $O(1/T^{1/3})$ rate for finding an approximate stationary point. Our work builds on the STORM algorithm, in conjunction with a novel approach to adaptively set the learning rate and momentum parameters.

On the Almost Sure Convergence of Stochastic Gradient Descent in Non-Convex Problems

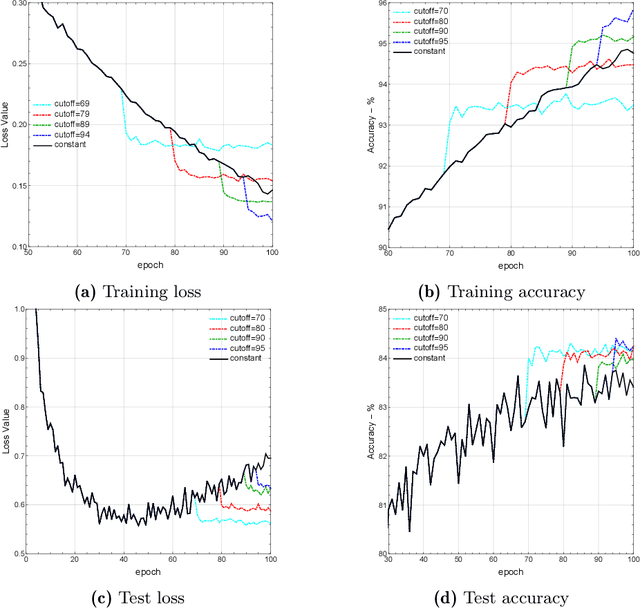
This paper analyzes the trajectories of stochastic gradient descent (SGD) to help understand the algorithm's convergence properties in non-convex problems. We first show that the sequence of iterates generated by SGD remains bounded and converges with probability $1$ under a very broad range of step-size schedules. Subsequently, going beyond existing positive probability guarantees, we show that SGD avoids strict saddle points/manifolds with probability $1$ for the entire spectrum of step-size policies considered. Finally, we prove that the algorithm's rate of convergence to Hurwicz minimizers is $\mathcal{O}(1/n^{p})$ if the method is employed with a $\Theta(1/n^p)$ step-size schedule. This provides an important guideline for tuning the algorithm's step-size as it suggests that a cool-down phase with a vanishing step-size could lead to faster convergence; we demonstrate this heuristic using ResNet architectures on CIFAR.

UniXGrad: A Universal, Adaptive Algorithm with Optimal Guarantees for Constrained Optimization

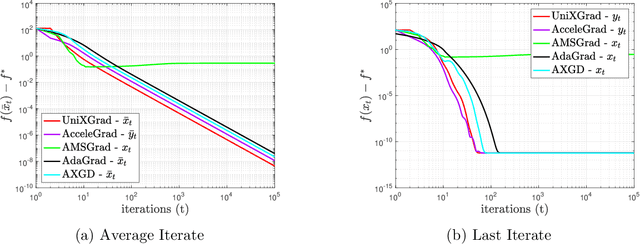
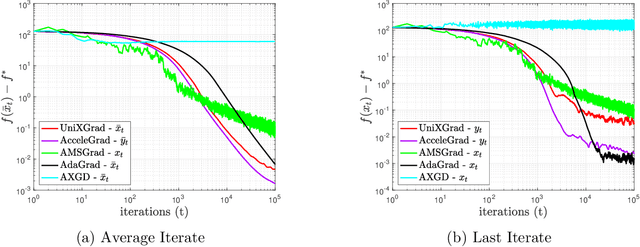
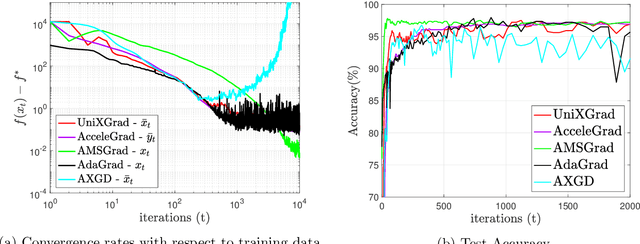
We propose a novel adaptive, accelerated algorithm for the stochastic constrained convex optimization setting. Our method, which is inspired by the Mirror-Prox method, \emph{simultaneously} achieves the optimal rates for smooth/non-smooth problems with either deterministic/stochastic first-order oracles. This is done without any prior knowledge of the smoothness nor the noise properties of the problem. To the best of our knowledge, this is the first adaptive, unified algorithm that achieves the optimal rates in the constrained setting. We demonstrate the practical performance of our framework through extensive numerical experiments.

Efficient learning of smooth probability functions from Bernoulli tests with guarantees

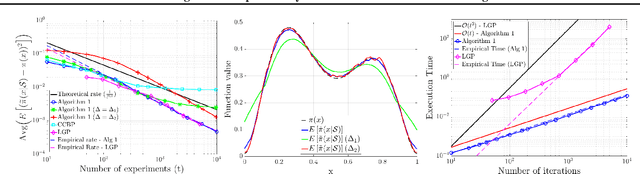
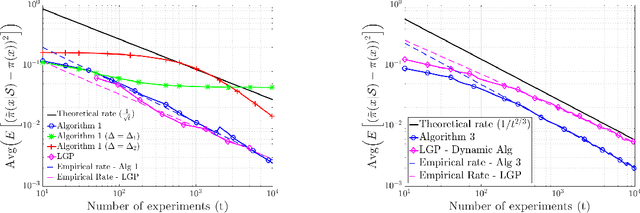
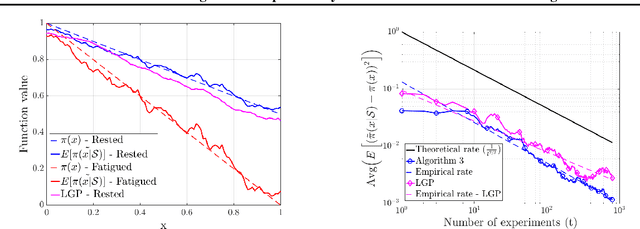
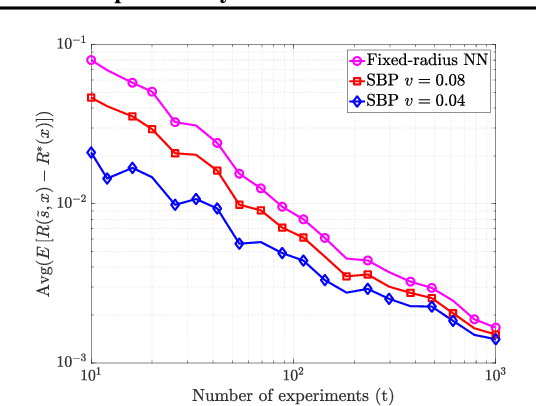
We study the fundamental problem of learning an unknown, smooth probability function via point-wise Bernoulli tests. We provide the first scalable algorithm for efficiently solving this problem with rigorous guarantees. In particular, we prove the convergence rate of our posterior update rule to the true probability function in L2-norm. Moreover, we allow the Bernoulli tests to depend on contextual features, and provide a modified inference engine with provable guarantees for this novel setting. Numerical results show that the empirical convergence rates match the theory, and illustrate the superiority of our approach in handling contextual features over the state-of-the-art.

Mirrored Langevin Dynamics

We consider the problem of sampling from constrained distributions, which has posed significant challenges to both non-asymptotic analysis and algorithmic design. We propose a unified framework, which is inspired by the classical mirror descent, to derive novel first-order sampling schemes. We prove that, for a general target distribution with strongly convex potential, our framework implies the existence of a first-order algorithm achieving $\tilde{O}(\epsilon^{-2}d)$ convergence, suggesting that the state-of-the-art $\tilde{O}(\epsilon^{-6}d^5)$ can be vastly improved. With the important Latent Dirichlet Allocation (LDA) application in mind, we specialize our algorithm to sample from Dirichlet posteriors, and derive the first non-asymptotic $\tilde{O}(\epsilon^{-2}d^2)$ rate for first-order sampling. We further extend our framework to the mini-batch setting and prove convergence rates when only stochastic gradients are available. Finally, we report promising experimental results for LDA on real datasets.