Improving SAM Requires Rethinking its Optimization Formulation

This paper rethinks Sharpness-Aware Minimization (SAM), which is originally formulated as a zero-sum game where the weights of a network and a bounded perturbation try to minimize/maximize, respectively, the same differentiable loss. To fundamentally improve this design, we argue that SAM should instead be reformulated using the 0-1 loss. As a continuous relaxation, we follow the simple conventional approach where the minimizing (maximizing) player uses an upper bound (lower bound) surrogate to the 0-1 loss. This leads to a novel formulation of SAM as a bilevel optimization problem, dubbed as BiSAM. BiSAM with newly designed lower-bound surrogate loss indeed constructs stronger perturbation. Through numerical evidence, we show that BiSAM consistently results in improved performance when compared to the original SAM and variants, while enjoying similar computational complexity. Our code is available at https://github.com/LIONS-EPFL/BiSAM.

Distributed Extra-gradient with Optimal Complexity and Communication Guarantees

We consider monotone variational inequality (VI) problems in multi-GPU settings where multiple processors/workers/clients have access to local stochastic dual vectors. This setting includes a broad range of important problems from distributed convex minimization to min-max and games. Extra-gradient, which is a de facto algorithm for monotone VI problems, has not been designed to be communication-efficient. To this end, we propose a quantized generalized extra-gradient (Q-GenX), which is an unbiased and adaptive compression method tailored to solve VIs. We provide an adaptive step-size rule, which adapts to the respective noise profiles at hand and achieve a fast rate of ${\mathcal O}(1/T)$ under relative noise, and an order-optimal ${\mathcal O}(1/\sqrt{T})$ under absolute noise and show distributed training accelerates convergence. Finally, we validate our theoretical results by providing real-world experiments and training generative adversarial networks on multiple GPUs.

Adaptive Stochastic Variance Reduction for Non-convex Finite-Sum Minimization

We propose an adaptive variance-reduction method, called AdaSpider, for minimization of $L$-smooth, non-convex functions with a finite-sum structure. In essence, AdaSpider combines an AdaGrad-inspired [Duchi et al., 2011, McMahan & Streeter, 2010], but a fairly distinct, adaptive step-size schedule with the recursive stochastic path integrated estimator proposed in [Fang et al., 2018]. To our knowledge, Adaspider is the first parameter-free non-convex variance-reduction method in the sense that it does not require the knowledge of problem-dependent parameters, such as smoothness constant $L$, target accuracy $\epsilon$ or any bound on gradient norms. In doing so, we are able to compute an $\epsilon$-stationary point with $\tilde{O}\left(n + \sqrt{n}/\epsilon^2\right)$ oracle-calls, which matches the respective lower bound up to logarithmic factors.

Extra-Newton: A First Approach to Noise-Adaptive Accelerated Second-Order Methods

This work proposes a universal and adaptive second-order method for minimizing second-order smooth, convex functions. Our algorithm achieves $O(\sigma / \sqrt{T})$ convergence when the oracle feedback is stochastic with variance $\sigma^2$, and improves its convergence to $O( 1 / T^3)$ with deterministic oracles, where $T$ is the number of iterations. Our method also interpolates these rates without knowing the nature of the oracle apriori, which is enabled by a parameter-free adaptive step-size that is oblivious to the knowledge of smoothness modulus, variance bounds and the diameter of the constrained set. To our knowledge, this is the first universal algorithm with such global guarantees within the second-order optimization literature.

No-Regret Learning in Games with Noisy Feedback: Faster Rates and Adaptivity via Learning Rate Separation

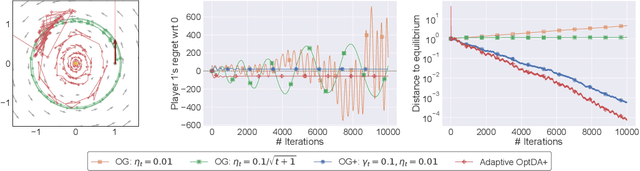
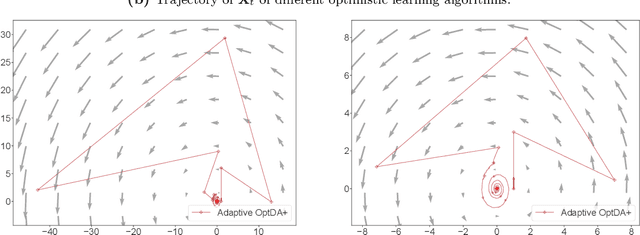
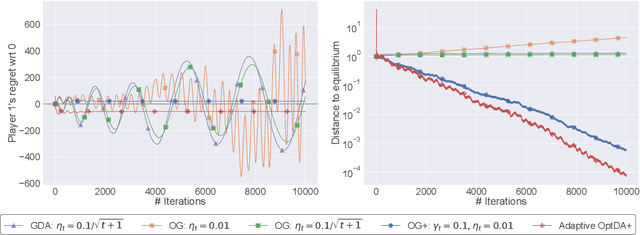
We examine the problem of regret minimization when the learner is involved in a continuous game with other optimizing agents: in this case, if all players follow a no-regret algorithm, it is possible to achieve significantly lower regret relative to fully adversarial environments. We study this problem in the context of variationally stable games (a class of continuous games which includes all convex-concave and monotone games), and when the players only have access to noisy estimates of their individual payoff gradients. If the noise is additive, the game-theoretic and purely adversarial settings enjoy similar regret guarantees; however, if the noise is multiplicative, we show that the learners can, in fact, achieve constant regret. We achieve this faster rate via an optimistic gradient scheme with learning rate separation -- that is, the method's extrapolation and update steps are tuned to different schedules, depending on the noise profile. Subsequently, to eliminate the need for delicate hyperparameter tuning, we propose a fully adaptive method that smoothly interpolates between worst- and best-case regret guarantees.

Adaptive first-order methods revisited: Convex optimization without Lipschitz requirements

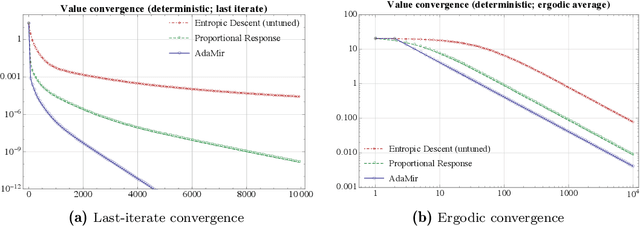
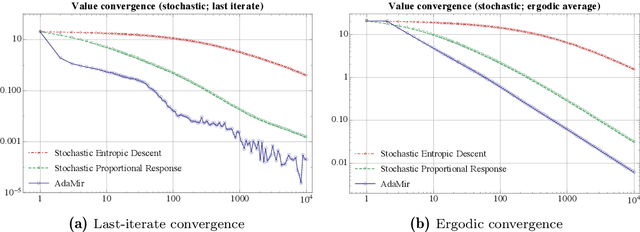
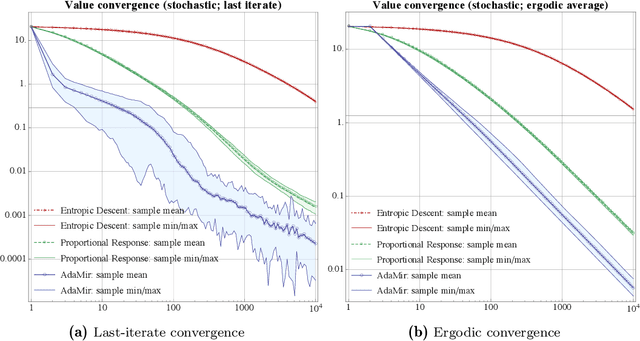
We propose a new family of adaptive first-order methods for a class of convex minimization problems that may fail to be Lipschitz continuous or smooth in the standard sense. Specifically, motivated by a recent flurry of activity on non-Lipschitz (NoLips) optimization, we consider problems that are continuous or smooth relative to a reference Bregman function - as opposed to a global, ambient norm (Euclidean or otherwise). These conditions encompass a wide range of problems with singular objectives, such as Fisher markets, Poisson tomography, D-design, and the like. In this setting, the application of existing order-optimal adaptive methods - like UnixGrad or AcceleGrad - is not possible, especially in the presence of randomness and uncertainty. The proposed method - which we call adaptive mirror descent (AdaMir) - aims to close this gap by concurrently achieving min-max optimal rates in problems that are relatively continuous or smooth, including stochastic ones.

Adaptive Learning in Continuous Games: Optimal Regret Bounds and Convergence to Nash Equilibrium

In game-theoretic learning, several agents are simultaneously following their individual interests, so the environment is non-stationary from each player's perspective. In this context, the performance of a learning algorithm is often measured by its regret. However, no-regret algorithms are not created equal in terms of game-theoretic guarantees: depending on how they are tuned, some of them may drive the system to an equilibrium, while others could produce cyclic, chaotic, or otherwise divergent trajectories. To account for this, we propose a range of no-regret policies based on optimistic mirror descent, with the following desirable properties: i) they do not require any prior tuning or knowledge of the game; ii) they all achieve O(\sqrt{T}) regret against arbitrary, adversarial opponents; and iii) they converge to the best response against convergent opponents. Also, if employed by all players, then iv) they guarantee O(1) social regret; while v) the induced sequence of play converges to Nash equilibrium with O(1) individual regret in all variationally stable games (a class of games that includes all monotone and convex-concave zero-sum games).

Adaptive extra-gradient methods for min-max optimization and games

We present a new family of min-max optimization algorithms that automatically exploit the geometry of the gradient data observed at earlier iterations to perform more informative extra-gradient steps in later ones. Thanks to this adaptation mechanism, the proposed methods automatically detect the problem's smoothness properties, without requiring any prior tuning by the optimizer. As a result, the algorithm simultaneously achieves the optimal smooth/non-smooth min-max convergence rates, i.e., it converges to an $\varepsilon$-optimal solution within $\mathcal{O}(1/\varepsilon)$ iterations in smooth problems, and within $\mathcal{O}(1/\varepsilon^2)$ iterations in non-smooth ones. Importantly, these guarantees do not require any of the standard boundedness or Lipschitz continuity conditions that are typically assumed in the literature; in particular, they apply even to problems with divergent loss functions (such as log-likelihood learning and the like). This "off-the-shelf" adaptation is achieved through the use of a geometric apparatus based on Finsler metrics and a suitably chosen mirror-prox template that allows us to derive sharp convergence rates for the family of methods at hand.