Stephen Roberts
Can convolutional ResNets approximately preserve input distances? A frequency analysis perspective
Jun 17, 2021

Abstract:ResNets constrained to be bi-Lipschitz, that is, approximately distance preserving, have been a crucial component of recently proposed techniques for deterministic uncertainty quantification in neural models. We show that theoretical justifications for recent regularisation schemes trying to enforce such a constraint suffer from a crucial flaw -- the theoretical link between the regularisation scheme used and bi-Lipschitzness is only valid under conditions which do not hold in practice, rendering existing theory of limited use, despite the strong empirical performance of these models. We provide a theoretical explanation for the effectiveness of these regularisation schemes using a frequency analysis perspective, showing that under mild conditions these schemes will enforce a lower Lipschitz bound on the low-frequency projection of images. We then provide empirical evidence supporting our theoretical claims, and perform further experiments which demonstrate that our broader conclusions appear to hold when some of the mathematical assumptions of our proof are relaxed, corresponding to the setup used in prior work. In addition, we present a simple constructive algorithm to search for counter examples to the distance preservation condition, and discuss possible implications of our theory for future model design.
Enhancing Cross-Sectional Currency Strategies by Ranking Refinement with Transformer-based Architectures
May 20, 2021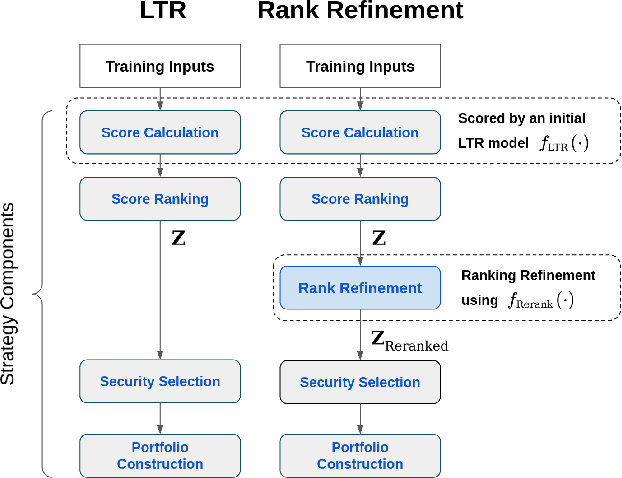
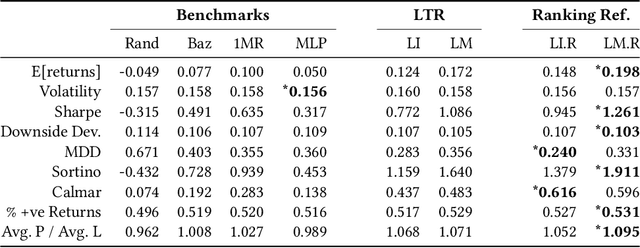
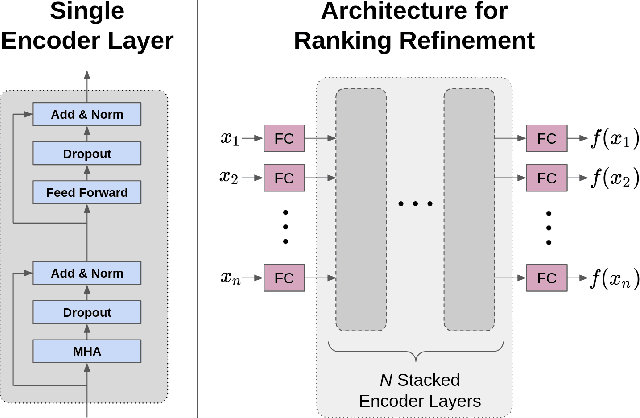
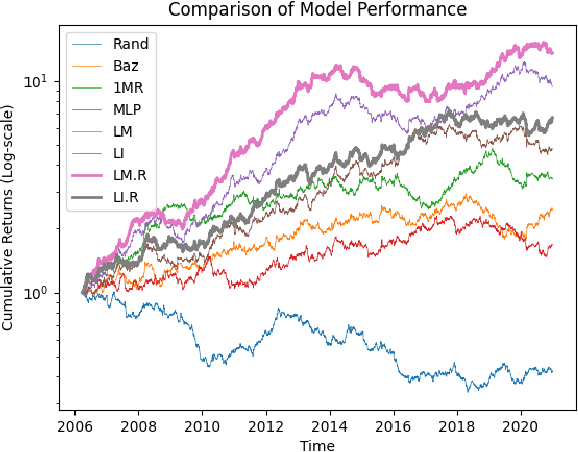
Abstract:The performance of a cross-sectional currency strategy depends crucially on accurately ranking instruments prior to portfolio construction. While this ranking step is traditionally performed using heuristics, or by sorting outputs produced by pointwise regression or classification models, Learning to Rank algorithms have recently presented themselves as competitive and viable alternatives. Despite improving ranking accuracy on average however, these techniques do not account for the possibility that assets positioned at the extreme ends of the ranked list -- which are ultimately used to construct the long/short portfolios -- can assume different distributions in the input space, and thus lead to sub-optimal strategy performance. Drawing from research in Information Retrieval that demonstrates the utility of contextual information embedded within top-ranked documents to learn the query's characteristics to improve ranking, we propose an analogous approach: exploiting the features of both out- and under-performing instruments to learn a model for refining the original ranked list. Under a re-ranking framework, we adapt the Transformer architecture to encode the features of extreme assets for refining our selection of long/short instruments obtained with an initial retrieval. Backtesting on a set of 31 currencies, our proposed methodology significantly boosts Sharpe ratios -- by approximately 20% over the original LTR algorithms and double that of traditional baselines.
Augmented World Models Facilitate Zero-Shot Dynamics Generalization From a Single Offline Environment
Apr 12, 2021
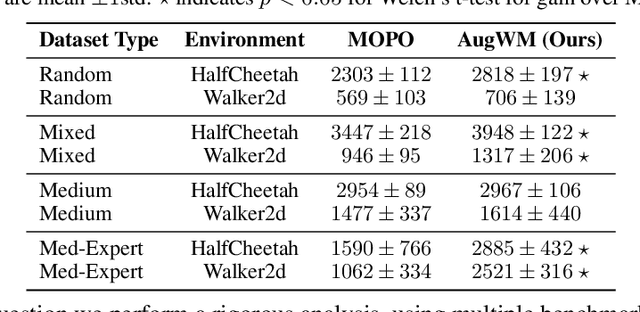

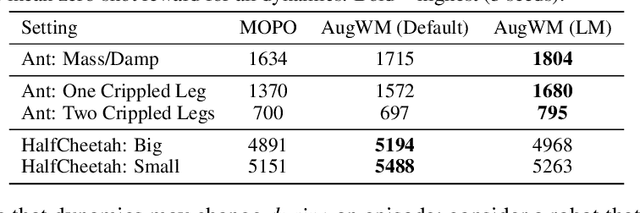
Abstract:Reinforcement learning from large-scale offline datasets provides us with the ability to learn policies without potentially unsafe or impractical exploration. Significant progress has been made in the past few years in dealing with the challenge of correcting for differing behavior between the data collection and learned policies. However, little attention has been paid to potentially changing dynamics when transferring a policy to the online setting, where performance can be up to 90% reduced for existing methods. In this paper we address this problem with Augmented World Models (AugWM). We augment a learned dynamics model with simple transformations that seek to capture potential changes in physical properties of the robot, leading to more robust policies. We not only train our policy in this new setting, but also provide it with the sampled augmentation as a context, allowing it to adapt to changes in the environment. At test time we learn the context in a self-supervised fashion by approximating the augmentation which corresponds to the new environment. We rigorously evaluate our approach on over 100 different changed dynamics settings, and show that this simple approach can significantly improve the zero-shot generalization of a recent state-of-the-art baseline, often achieving successful policies where the baseline fails.
Adversarial Robustness Guarantees for Gaussian Processes
Apr 07, 2021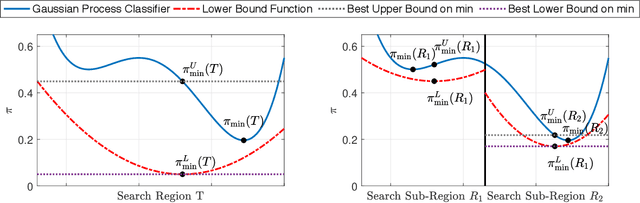
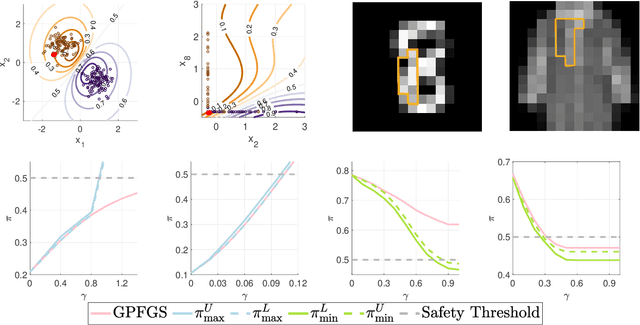
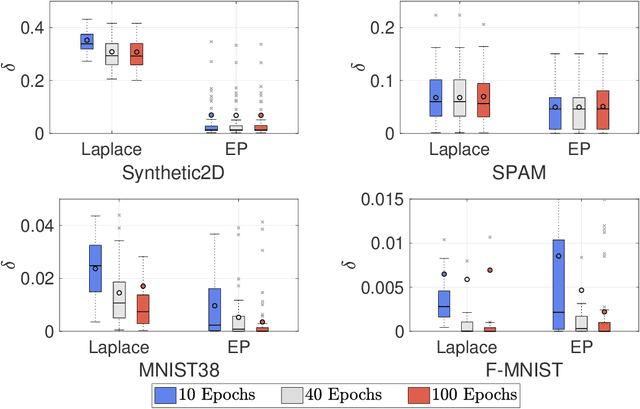
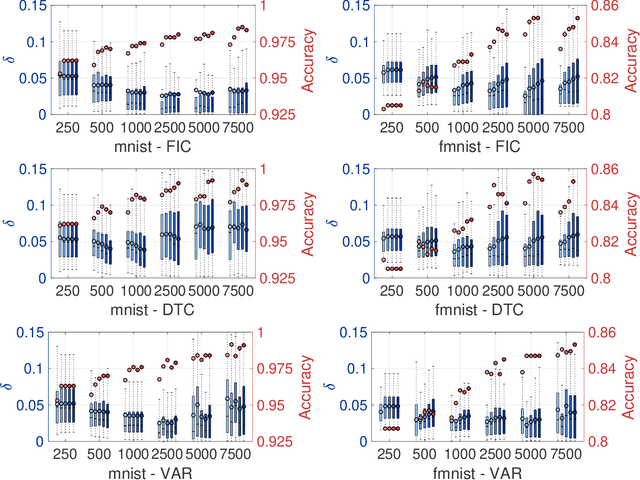
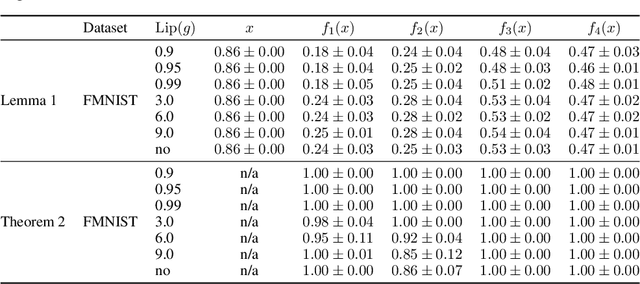
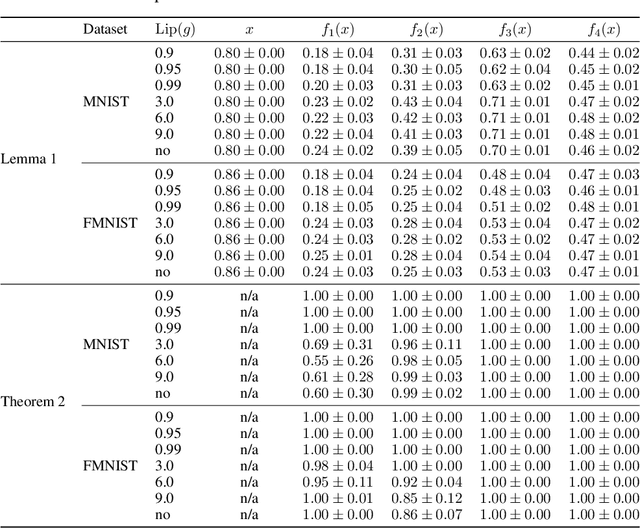
Abstract:Gaussian processes (GPs) enable principled computation of model uncertainty, making them attractive for safety-critical applications. Such scenarios demand that GP decisions are not only accurate, but also robust to perturbations. In this paper we present a framework to analyse adversarial robustness of GPs, defined as invariance of the model's decision to bounded perturbations. Given a compact subset of the input space $T\subseteq \mathbb{R}^d$, a point $x^*$ and a GP, we provide provable guarantees of adversarial robustness of the GP by computing lower and upper bounds on its prediction range in $T$. We develop a branch-and-bound scheme to refine the bounds and show, for any $\epsilon > 0$, that our algorithm is guaranteed to converge to values $\epsilon$-close to the actual values in finitely many iterations. The algorithm is anytime and can handle both regression and classification tasks, with analytical formulation for most kernels used in practice. We evaluate our methods on a collection of synthetic and standard benchmark datasets, including SPAM, MNIST and FashionMNIST. We study the effect of approximate inference techniques on robustness and demonstrate how our method can be used for interpretability. Our empirical results suggest that the adversarial robustness of GPs increases with accurate posterior estimation.
Building Cross-Sectional Systematic Strategies By Learning to Rank
Dec 13, 2020Abstract:The success of a cross-sectional systematic strategy depends critically on accurately ranking assets prior to portfolio construction. Contemporary techniques perform this ranking step either with simple heuristics or by sorting outputs from standard regression or classification models, which have been demonstrated to be sub-optimal for ranking in other domains (e.g. information retrieval). To address this deficiency, we propose a framework to enhance cross-sectional portfolios by incorporating learning-to-rank algorithms, which lead to improvements of ranking accuracy by learning pairwise and listwise structures across instruments. Using cross-sectional momentum as a demonstrative case study, we show that the use of modern machine learning ranking algorithms can substantially improve the trading performance of cross-sectional strategies -- providing approximately threefold boosting of Sharpe Ratios compared to traditional approaches.
Explaining the Adaptive Generalisation Gap
Nov 15, 2020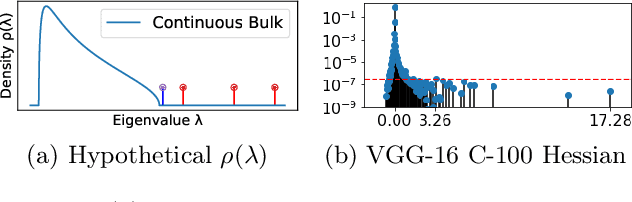

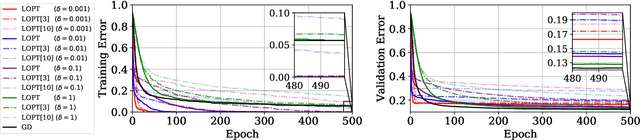
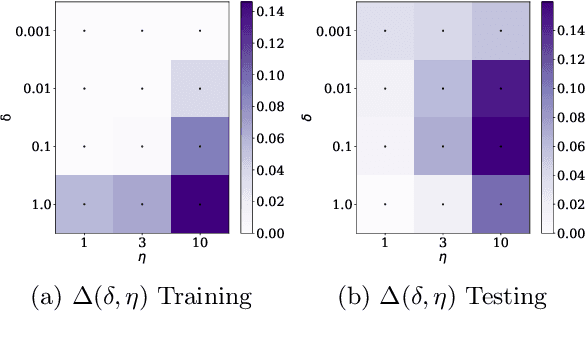
Abstract:We conjecture that the reason for the difference in generalisation between adaptive and non adaptive gradient methods stems from the failure of adaptive methods to account for the greater levels of noise associated with flatter directions in their estimates of local curvature. This conjecture motivated by results in random matrix theory has implications for optimisation in both simple convex settings and deep neural networks. We demonstrate that typical schedules used for adaptive methods (with low numerical stability or damping constants) serve to bias relative movement towards flat directions relative to sharp directions, effectively amplifying the noise-to-signal ratio and harming generalisation. We show that the numerical stability/damping constant used in these methods can be decomposed into a learning rate reduction and linear shrinkage of the estimated curvature matrix. We then demonstrate significant generalisation improvements by increasing the shrinkage coefficient, closing the generalisation gap entirely in our neural network experiments. Finally, we show that other popular modifications to adaptive methods, such as decoupled weight decay and partial adaptivity can be shown to calibrate parameter updates to make better use of sharper, more reliable directions.
SafePILCO: a software tool for safe and data-efficient policy synthesis
Aug 07, 2020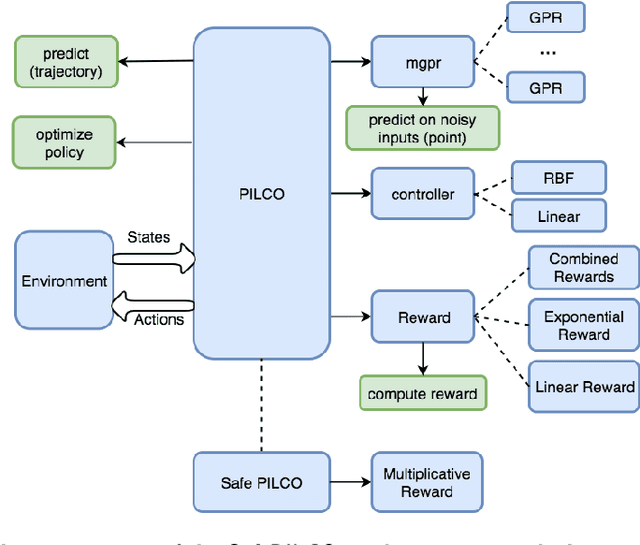
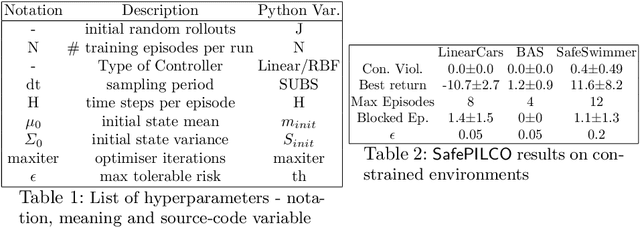
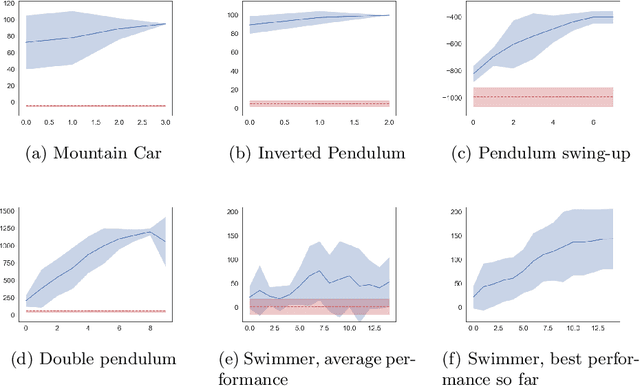
Abstract:SafePILCO is a software tool for safe and data-efficient policy search with reinforcement learning. It extends the known PILCO algorithm, originally written in MATLAB, to support safe learning. We provide a Python implementation and leverage existing libraries that allow the codebase to remain short and modular, which is appropriate for wider use by the verification, reinforcement learning, and control communities.
Explicit Regularisation in Gaussian Noise Injections
Jul 14, 2020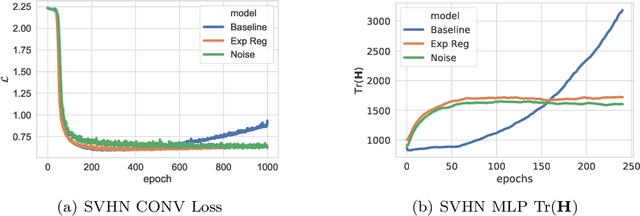
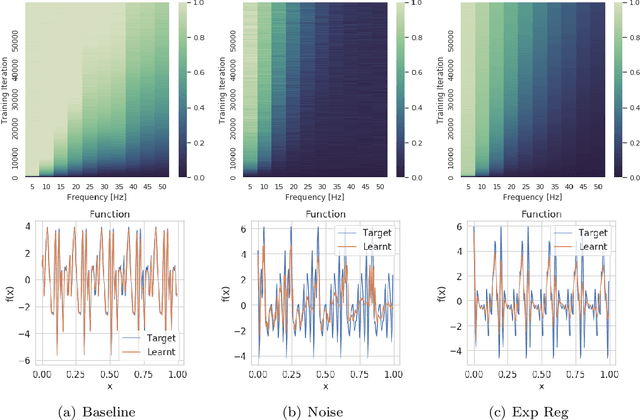
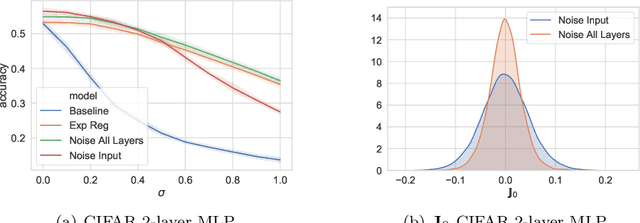
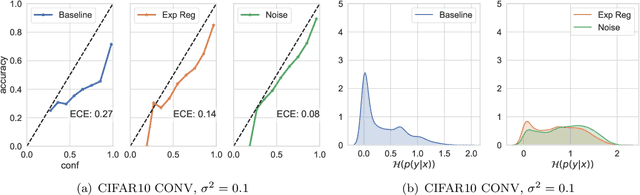
Abstract:We study the regularisation induced in neural networks by Gaussian noise injections (GNIs). Though such injections have been extensively studied when applied to data, there have been few studies on understanding the regularising effect they induce when applied to network activations. Here we derive the explicit regulariser of GNIs, obtained by marginalising out the injected noise, and show that it is a form of Tikhonov regularisation which penalises functions with high-frequency components in the Fourier domain. We show analytically and empirically that such regularisation produces calibrated classifiers with large classification margins and that the explicit regulariser we derive is able to reproduce these effects.
Towards a Theoretical Understanding of the Robustness of Variational Autoencoders
Jul 14, 2020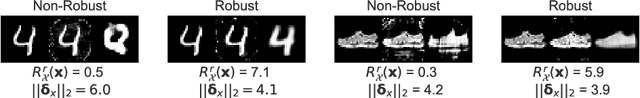

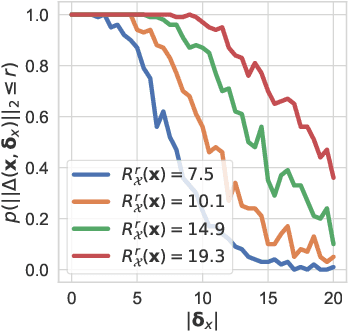
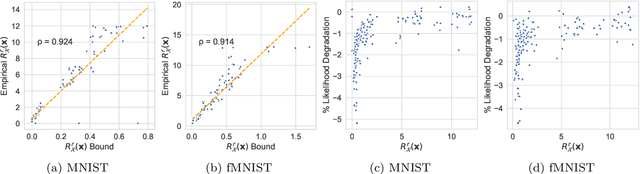
Abstract:We make inroads into understanding the robustness of Variational Autoencoders (VAEs) to adversarial attacks and other input perturbations. While previous work has developed algorithmic approaches to attacking and defending VAEs, there remains a lack of formalization for what it means for a VAE to be robust. To address this, we develop a novel criterion for robustness in probabilistic models: $r$-robustness. We then use this to construct the first theoretical results for the robustness of VAEs, deriving margins in the input space for which we can provide guarantees about the resulting reconstruction. Informally, we are able to define a region within which any perturbation will produce a reconstruction that is similar to the original reconstruction. To support our analysis, we show that VAEs trained using disentangling methods not only score well under our robustness metrics, but that the reasons for this can be interpreted through our theoretical results.
Relaxed-Responsibility Hierarchical Discrete VAEs
Jul 14, 2020
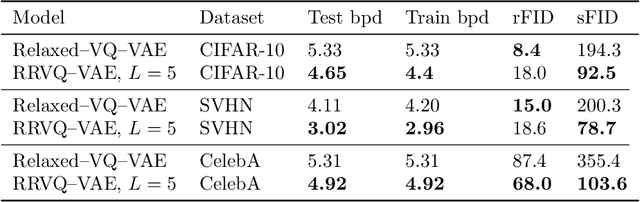
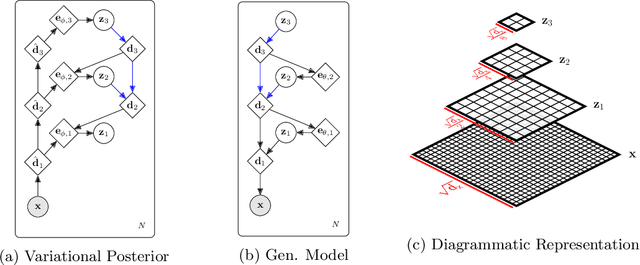

Abstract:Successfully training Variational Autoencoders (VAEs) with a hierarchy of discrete latent variables remains an area of active research. Leveraging insights from classical methods of inference we introduce $\textit{Relaxed-Responsibility Vector-Quantisation}$, a novel way to parameterise discrete latent variables, a refinement of relaxed Vector-Quantisation. This enables a novel approach to hierarchical discrete variational autoencoder with numerous layers of latent variables that we train end-to-end. Unlike discrete VAEs with a single layer of latent variables, we can produce realistic-looking samples by ancestral sampling: it is not essential to train a second generative model over the learnt latent representations to then sample from and then decode. Further, we observe different layers of our model become associated with different aspects of the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge