A Closer Look at Memorization in Deep Networks

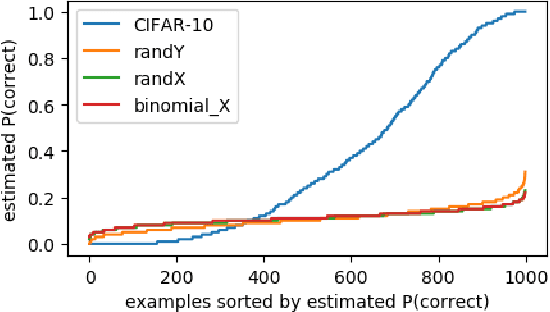
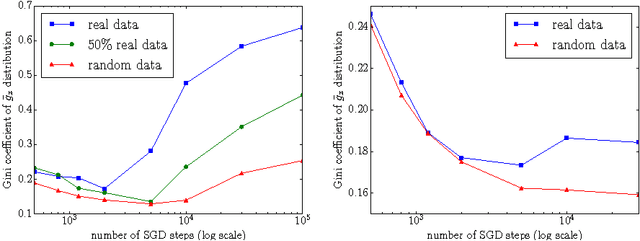
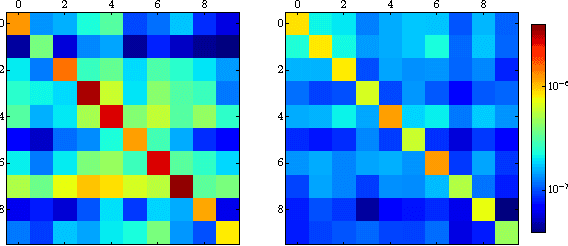
We examine the role of memorization in deep learning, drawing connections to capacity, generalization, and adversarial robustness. While deep networks are capable of memorizing noise data, our results suggest that they tend to prioritize learning simple patterns first. In our experiments, we expose qualitative differences in gradient-based optimization of deep neural networks (DNNs) on noise vs. real data. We also demonstrate that for appropriately tuned explicit regularization (e.g., dropout) we can degrade DNN training performance on noise datasets without compromising generalization on real data. Our analysis suggests that the notions of effective capacity which are dataset independent are unlikely to explain the generalization performance of deep networks when trained with gradient based methods because training data itself plays an important role in determining the degree of memorization.

Frank-Wolfe Algorithms for Saddle Point Problems

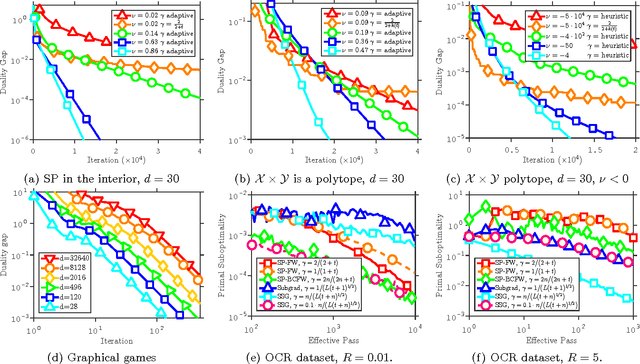
We extend the Frank-Wolfe (FW) optimization algorithm to solve constrained smooth convex-concave saddle point (SP) problems. Remarkably, the method only requires access to linear minimization oracles. Leveraging recent advances in FW optimization, we provide the first proof of convergence of a FW-type saddle point solver over polytopes, thereby partially answering a 30 year-old conjecture. We also survey other convergence results and highlight gaps in the theoretical underpinnings of FW-style algorithms. Motivating applications without known efficient alternatives are explored through structured prediction with combinatorial penalties as well as games over matching polytopes involving an exponential number of constraints.

PAC-Bayesian Theory Meets Bayesian Inference

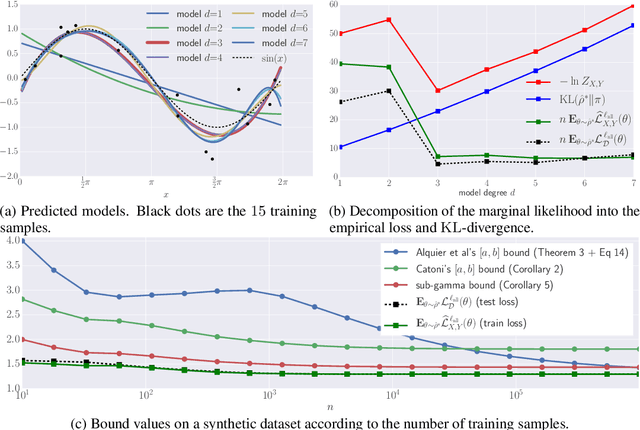
We exhibit a strong link between frequentist PAC-Bayesian risk bounds and the Bayesian marginal likelihood. That is, for the negative log-likelihood loss function, we show that the minimization of PAC-Bayesian generalization risk bounds maximizes the Bayesian marginal likelihood. This provides an alternative explanation to the Bayesian Occam's razor criteria, under the assumption that the data is generated by an i.i.d distribution. Moreover, as the negative log-likelihood is an unbounded loss function, we motivate and propose a PAC-Bayesian theorem tailored for the sub-gamma loss family, and we show that our approach is sound on classical Bayesian linear regression tasks.

Convergence Rate of Frank-Wolfe for Non-Convex Objectives

We give a simple proof that the Frank-Wolfe algorithm obtains a stationary point at a rate of $O(1/\sqrt{t})$ on non-convex objectives with a Lipschitz continuous gradient. Our analysis is affine invariant and is the first, to the best of our knowledge, giving a similar rate to what was already proven for projected gradient methods (though on slightly different measures of stationarity).

Unsupervised Learning from Narrated Instruction Videos

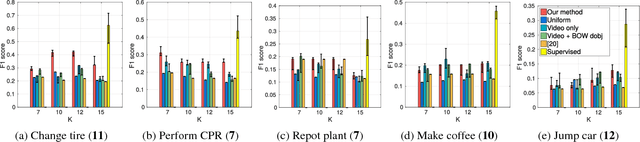
We address the problem of automatically learning the main steps to complete a certain task, such as changing a car tire, from a set of narrated instruction videos. The contributions of this paper are three-fold. First, we develop a new unsupervised learning approach that takes advantage of the complementary nature of the input video and the associated narration. The method solves two clustering problems, one in text and one in video, applied one after each other and linked by joint constraints to obtain a single coherent sequence of steps in both modalities. Second, we collect and annotate a new challenging dataset of real-world instruction videos from the Internet. The dataset contains about 800,000 frames for five different tasks that include complex interactions between people and objects, and are captured in a variety of indoor and outdoor settings. Third, we experimentally demonstrate that the proposed method can automatically discover, in an unsupervised manner, the main steps to achieve the task and locate the steps in the input videos.

Beyond CCA: Moment Matching for Multi-View Models

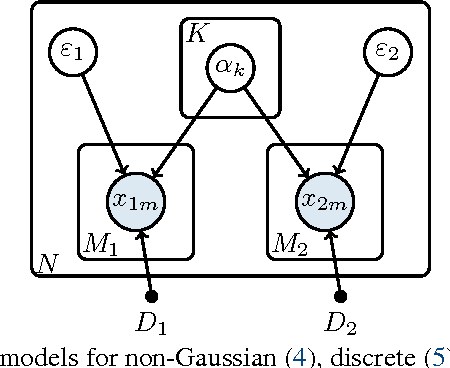
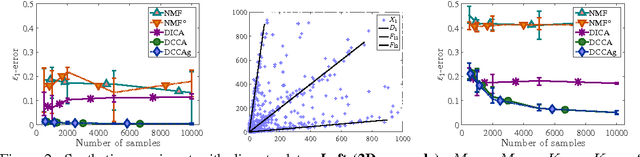
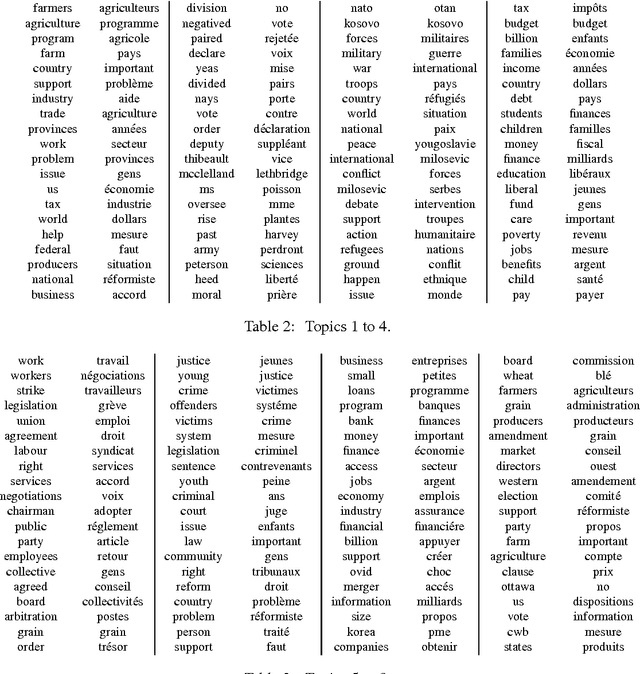
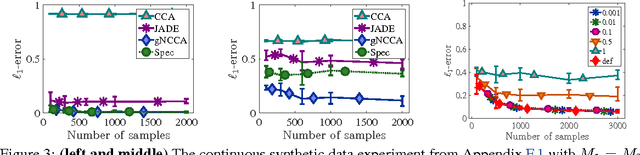
We introduce three novel semi-parametric extensions of probabilistic canonical correlation analysis with identifiability guarantees. We consider moment matching techniques for estimation in these models. For that, by drawing explicit links between the new models and a discrete version of independent component analysis (DICA), we first extend the DICA cumulant tensors to the new discrete version of CCA. By further using a close connection with independent component analysis, we introduce generalized covariance matrices, which can replace the cumulant tensors in the moment matching framework, and, therefore, improve sample complexity and simplify derivations and algorithms significantly. As the tensor power method or orthogonal joint diagonalization are not applicable in the new setting, we use non-orthogonal joint diagonalization techniques for matching the cumulants. We demonstrate performance of the proposed models and estimation techniques on experiments with both synthetic and real datasets.

Minding the Gaps for Block Frank-Wolfe Optimization of Structured SVMs

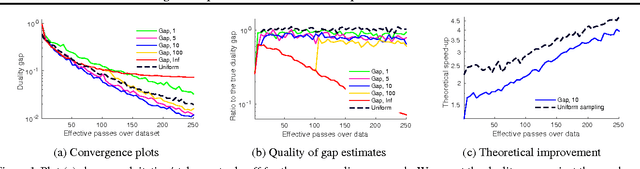
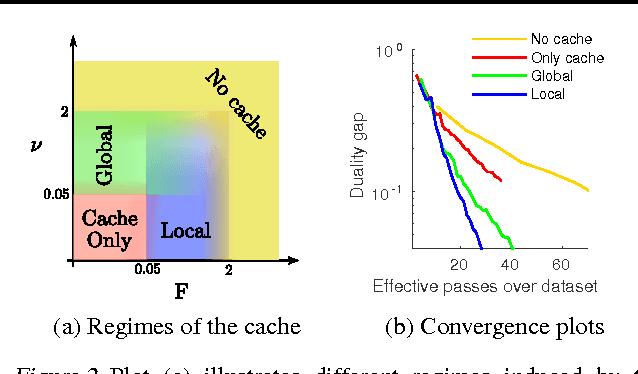
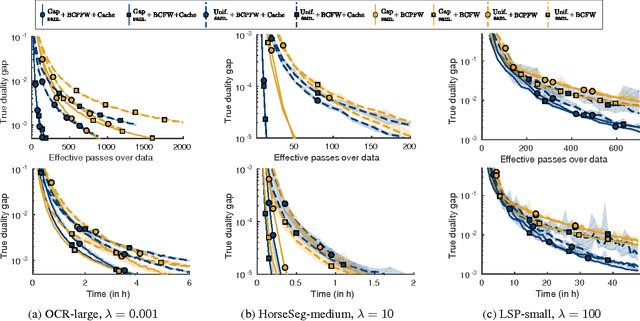
In this paper, we propose several improvements on the block-coordinate Frank-Wolfe (BCFW) algorithm from Lacoste-Julien et al. (2013) recently used to optimize the structured support vector machine (SSVM) objective in the context of structured prediction, though it has wider applications. The key intuition behind our improvements is that the estimates of block gaps maintained by BCFW reveal the block suboptimality that can be used as an adaptive criterion. First, we sample objects at each iteration of BCFW in an adaptive non-uniform way via gapbased sampling. Second, we incorporate pairwise and away-step variants of Frank-Wolfe into the block-coordinate setting. Third, we cache oracle calls with a cache-hit criterion based on the block gaps. Fourth, we provide the first method to compute an approximate regularization path for SSVM. Finally, we provide an exhaustive empirical evaluation of all our methods on four structured prediction datasets.

Variance Reduced Stochastic Gradient Descent with Neighbors

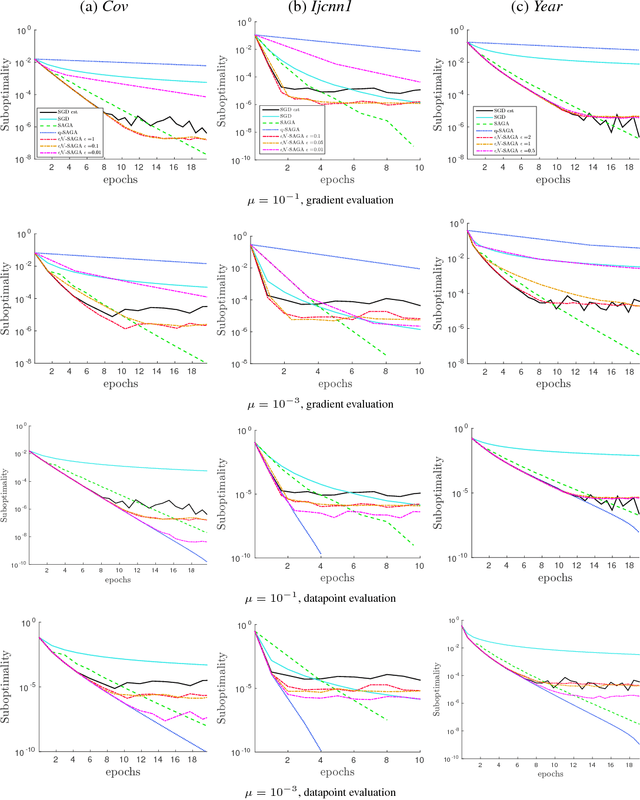
Stochastic Gradient Descent (SGD) is a workhorse in machine learning, yet its slow convergence can be a computational bottleneck. Variance reduction techniques such as SAG, SVRG and SAGA have been proposed to overcome this weakness, achieving linear convergence. However, these methods are either based on computations of full gradients at pivot points, or on keeping per data point corrections in memory. Therefore speed-ups relative to SGD may need a minimal number of epochs in order to materialize. This paper investigates algorithms that can exploit neighborhood structure in the training data to share and re-use information about past stochastic gradients across data points, which offers advantages in the transient optimization phase. As a side-product we provide a unified convergence analysis for a family of variance reduction algorithms, which we call memorization algorithms. We provide experimental results supporting our theory.

Barrier Frank-Wolfe for Marginal Inference

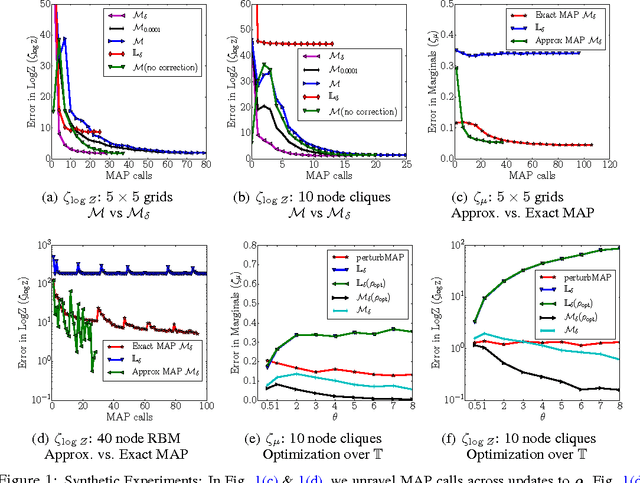
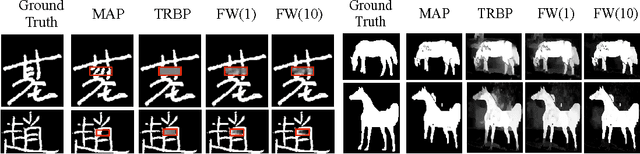
We introduce a globally-convergent algorithm for optimizing the tree-reweighted (TRW) variational objective over the marginal polytope. The algorithm is based on the conditional gradient method (Frank-Wolfe) and moves pseudomarginals within the marginal polytope through repeated maximum a posteriori (MAP) calls. This modular structure enables us to leverage black-box MAP solvers (both exact and approximate) for variational inference, and obtains more accurate results than tree-reweighted algorithms that optimize over the local consistency relaxation. Theoretically, we bound the sub-optimality for the proposed algorithm despite the TRW objective having unbounded gradients at the boundary of the marginal polytope. Empirically, we demonstrate the increased quality of results found by tightening the relaxation over the marginal polytope as well as the spanning tree polytope on synthetic and real-world instances.

On the Global Linear Convergence of Frank-Wolfe Optimization Variants

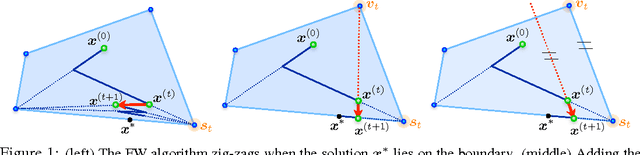
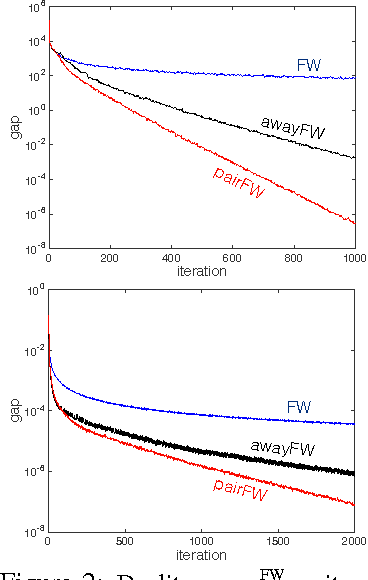
The Frank-Wolfe (FW) optimization algorithm has lately re-gained popularity thanks in particular to its ability to nicely handle the structured constraints appearing in machine learning applications. However, its convergence rate is known to be slow (sublinear) when the solution lies at the boundary. A simple less-known fix is to add the possibility to take 'away steps' during optimization, an operation that importantly does not require a feasibility oracle. In this paper, we highlight and clarify several variants of the Frank-Wolfe optimization algorithm that have been successfully applied in practice: away-steps FW, pairwise FW, fully-corrective FW and Wolfe's minimum norm point algorithm, and prove for the first time that they all enjoy global linear convergence, under a weaker condition than strong convexity of the objective. The constant in the convergence rate has an elegant interpretation as the product of the (classical) condition number of the function with a novel geometric quantity that plays the role of a 'condition number' of the constraint set. We provide pointers to where these algorithms have made a difference in practice, in particular with the flow polytope, the marginal polytope and the base polytope for submodular optimization.