Sample Compression Hypernetworks: From Generalization Bounds to Meta-Learning

Reconstruction functions are pivotal in sample compression theory, a framework for deriving tight generalization bounds. From a small sample of the training set (the compression set) and an optional stream of information (the message), they recover a predictor previously learned from the whole training set. While usually fixed, we propose to learn reconstruction functions. To facilitate the optimization and increase the expressiveness of the message, we derive a new sample compression generalization bound for real-valued messages. From this theoretical analysis, we then present a new hypernetwork architecture that outputs predictors with tight generalization guarantees when trained using an original meta-learning framework. The results of promising preliminary experiments are then reported.

Sample compression unleashed : New generalization bounds for real valued losses

The sample compression theory provides generalization guarantees for predictors that can be fully defined using a subset of the training dataset and a (short) message string, generally defined as a binary sequence. Previous works provided generalization bounds for the zero-one loss, which is restrictive, notably when applied to deep learning approaches. In this paper, we present a general framework for deriving new sample compression bounds that hold for real-valued losses. We empirically demonstrate the tightness of the bounds and their versatility by evaluating them on different types of models, e.g., neural networks and decision forests, trained with the Pick-To-Learn (P2L) meta-algorithm, which transforms the training method of any machine-learning predictor to yield sample-compressed predictors. In contrast to existing P2L bounds, ours are valid in the non-consistent case.

Phoneme Discretized Saliency Maps for Explainable Detection of AI-Generated Voice

In this paper, we propose Phoneme Discretized Saliency Maps (PDSM), a discretization algorithm for saliency maps that takes advantage of phoneme boundaries for explainable detection of AI-generated voice. We experimentally show with two different Text-to-Speech systems (i.e., Tacotron2 and Fastspeech2) that the proposed algorithm produces saliency maps that result in more faithful explanations compared to standard posthoc explanation methods. Moreover, by associating the saliency maps to the phoneme representations, this methodology generates explanations that tend to be more understandable than standard saliency maps on magnitude spectrograms.

Interpretability in Machine Learning: on the Interplay with Explainability, Predictive Performances and Models

Interpretability has recently gained attention in the field of machine learning, for it is crucial when it comes to high-stakes decisions or troubleshooting. This abstract concept is hard to grasp and has been associated, over time, with many labels and preconceived ideas. In this position paper, in order to clarify some misunderstandings regarding interpretability, we discuss its relationship with significant concepts in machine learning: explainability, predictive performances, and machine learning models. For instance, we challenge the idea that interpretability and explainability are substitutes to one another, or that a fixed degree of interpretability can be associated with a given machine learning model.

Statistical Guarantees for Variational Autoencoders using PAC-Bayesian Theory

Since their inception, Variational Autoencoders (VAEs) have become central in machine learning. Despite their widespread use, numerous questions regarding their theoretical properties remain open. Using PAC-Bayesian theory, this work develops statistical guarantees for VAEs. First, we derive the first PAC-Bayesian bound for posterior distributions conditioned on individual samples from the data-generating distribution. Then, we utilize this result to develop generalization guarantees for the VAE's reconstruction loss, as well as upper bounds on the distance between the input and the regenerated distributions. More importantly, we provide upper bounds on the Wasserstein distance between the input distribution and the distribution defined by the VAE's generative model.

Invariant Causal Set Covering Machines

Rule-based models, such as decision trees, appeal to practitioners due to their interpretable nature. However, the learning algorithms that produce such models are often vulnerable to spurious associations and thus, they are not guaranteed to extract causally-relevant insights. In this work, we build on ideas from the invariant causal prediction literature to propose Invariant Causal Set Covering Machines, an extension of the classical Set Covering Machine algorithm for conjunctions/disjunctions of binary-valued rules that provably avoids spurious associations. We demonstrate both theoretically and empirically that our method can identify the causal parents of a variable of interest in polynomial time.

PAC-Bayesian Generalization Bounds for Adversarial Generative Models

We extend PAC-Bayesian theory to generative models and develop generalization bounds for models based on the Wasserstein distance and the total variation distance. Our first result on the Wasserstein distance assumes the instance space is bounded, while our second result takes advantage of dimensionality reduction. Our results naturally apply to Wasserstein GANs and Energy-Based GANs, and our bounds provide new training objectives for these two. Although our work is mainly theoretical, we perform numerical experiments showing non-vacuous generalization bounds for Wasserstein GANs on synthetic datasets.

A Greedy Algorithm for Building Compact Binary Activated Neural Networks

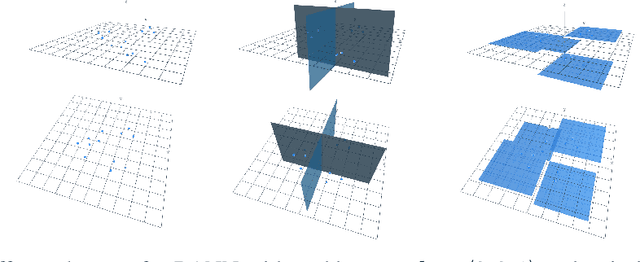
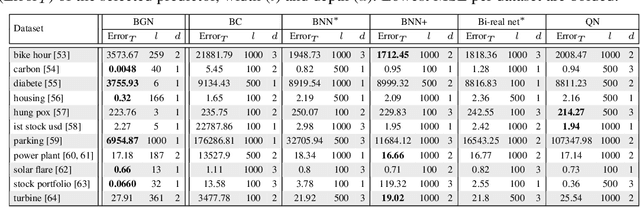
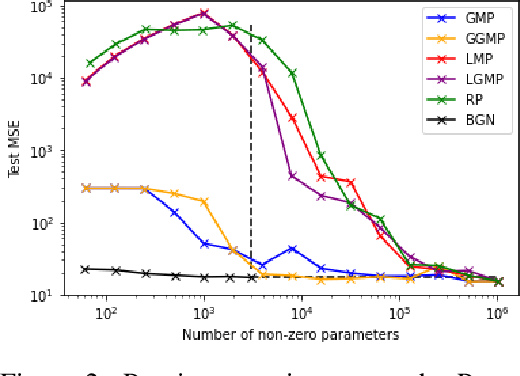
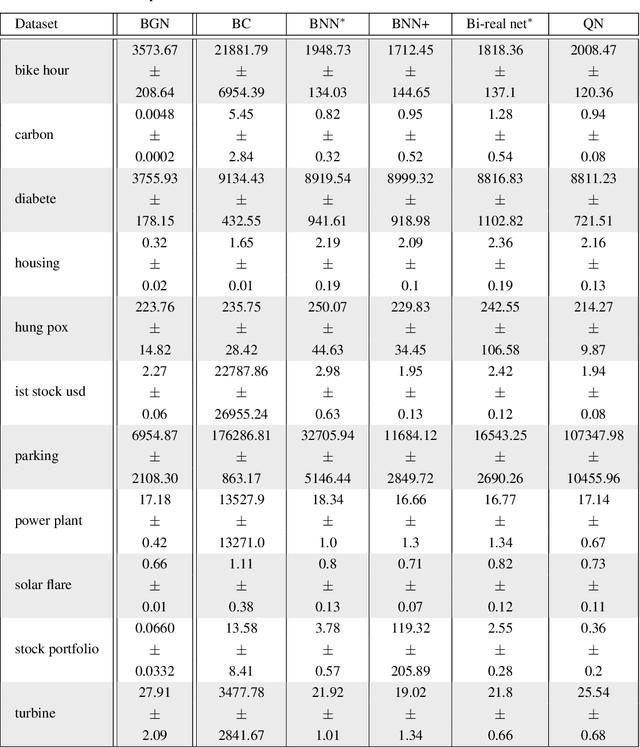
We study binary activated neural networks in the context of regression tasks, provide guarantees on the expressiveness of these particular networks and propose a greedy algorithm for building such networks. Aiming for predictors having small resources needs, the greedy approach does not need to fix in advance an architecture for the network: this one is built one layer at a time, one neuron at a time, leading to predictors that aren't needlessly wide and deep for a given task. Similarly to boosting algorithms, our approach guarantees a training loss reduction every time a neuron is added to a layer. This greatly differs from most binary activated neural networks training schemes that rely on stochastic gradient descent (circumventing the 0-almost-everywhere derivative problem of the binary activation function by surrogates such as the straight through estimator or continuous binarization). We show that our method provides compact and sparse predictors while obtaining similar performances to state-of-the-art methods for training binary activated networks.

Learning Aggregations of Binary Activated Neural Networks with Probabilities over Representations

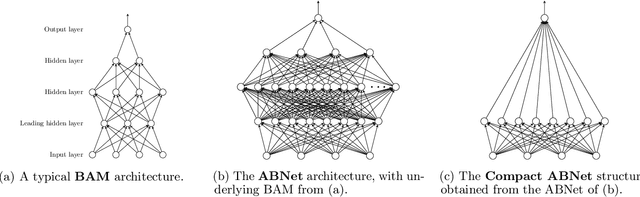
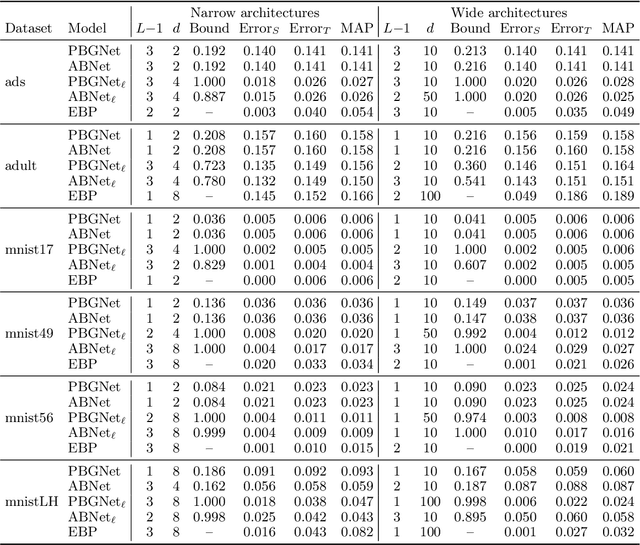
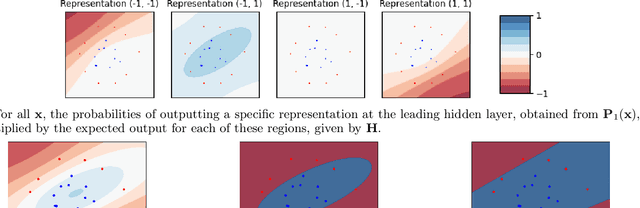
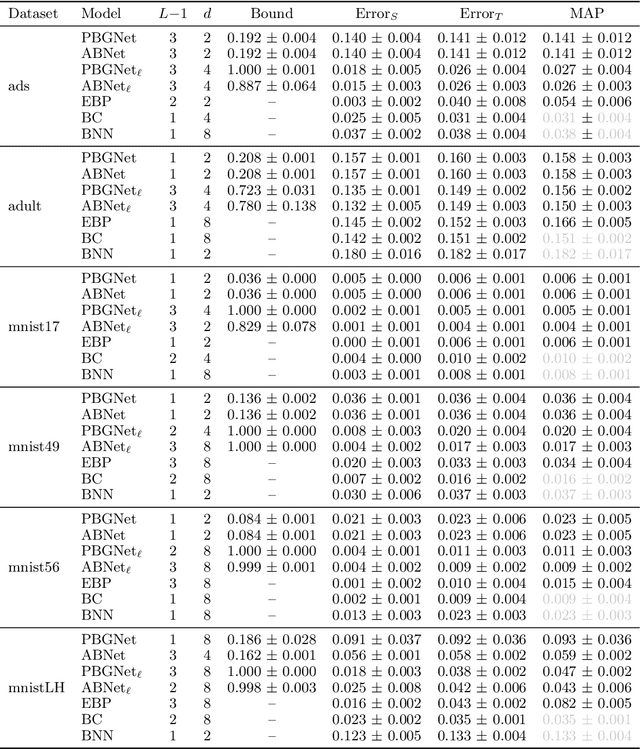
Considering a probability distribution over parameters is known as an efficient strategy to learn a neural network with non-differentiable activation functions. We study the expectation of a probabilistic neural network as a predictor by itself, focusing on the aggregation of binary activated neural networks with normal distributions over real-valued weights. Our work leverages a recent analysis derived from the PAC-Bayesian framework that derives tight generalization bounds and learning procedures for the expected output value of such an aggregation, which is given by an analytical expression. While the combinatorial nature of the latter has been circumvented by approximations in previous works, we show that the exact computation remains tractable for deep but narrow neural networks, thanks to a dynamic programming approach. This leads us to a peculiar bound minimization learning algorithm for binary activated neural networks, where the forward pass propagates probabilities over representations instead of activation values. A stochastic counterpart of this new neural networks training scheme that scales to wider architectures is proposed.

Learning Stochastic Majority Votes by Minimizing a PAC-Bayes Generalization Bound

We investigate a stochastic counterpart of majority votes over finite ensembles of classifiers, and study its generalization properties. While our approach holds for arbitrary distributions, we instantiate it with Dirichlet distributions: this allows for a closed-form and differentiable expression for the expected risk, which then turns the generalization bound into a tractable training objective. The resulting stochastic majority vote learning algorithm achieves state-of-the-art accuracy and benefits from (non-vacuous) tight generalization bounds, in a series of numerical experiments when compared to competing algorithms which also minimize PAC-Bayes objectives -- both with uninformed (data-independent) and informed (data-dependent) priors.