Discounted Online Convex Optimization: Uniform Regret Across a Continuous Interval

Reflecting the greater significance of recent history over the distant past in non-stationary environments, $\lambda$-discounted regret has been introduced in online convex optimization (OCO) to gracefully forget past data as new information arrives. When the discount factor $\lambda$ is given, online gradient descent with an appropriate step size achieves an $O(1/\sqrt{1-\lambda})$ discounted regret. However, the value of $\lambda$ is often not predetermined in real-world scenarios. This gives rise to a significant open question: is it possible to develop a discounted algorithm that adapts to an unknown discount factor. In this paper, we affirmatively answer this question by providing a novel analysis to demonstrate that smoothed OGD (SOGD) achieves a uniform $O(\sqrt{\log T/1-\lambda})$ discounted regret, holding for all values of $\lambda$ across a continuous interval simultaneously. The basic idea is to maintain multiple OGD instances to handle different discount factors, and aggregate their outputs sequentially by an online prediction algorithm named as Discounted-Normal-Predictor (DNP) (Kapralov and Panigrahy,2010). Our analysis reveals that DNP can combine the decisions of two experts, even when they operate on discounted regret with different discount factors.

Learning without Isolation: Pathway Protection for Continual Learning

Deep networks are prone to catastrophic forgetting during sequential task learning, i.e., losing the knowledge about old tasks upon learning new tasks. To this end, continual learning(CL) has emerged, whose existing methods focus mostly on regulating or protecting the parameters associated with the previous tasks. However, parameter protection is often impractical, since the size of parameters for storing the old-task knowledge increases linearly with the number of tasks, otherwise it is hard to preserve the parameters related to the old-task knowledge. In this work, we bring a dual opinion from neuroscience and physics to CL: in the whole networks, the pathways matter more than the parameters when concerning the knowledge acquired from the old tasks. Following this opinion, we propose a novel CL framework, learning without isolation(LwI), where model fusion is formulated as graph matching and the pathways occupied by the old tasks are protected without being isolated. Thanks to the sparsity of activation channels in a deep network, LwI can adaptively allocate available pathways for a new task, realizing pathway protection and addressing catastrophic forgetting in a parameter-efficient manner. Experiments on popular benchmark datasets demonstrate the superiority of the proposed LwI.

Projection-Free Variance Reduction Methods for Stochastic Constrained Multi-Level Compositional Optimization

This paper investigates projection-free algorithms for stochastic constrained multi-level optimization. In this context, the objective function is a nested composition of several smooth functions, and the decision set is closed and convex. Existing projection-free algorithms for solving this problem suffer from two limitations: 1) they solely focus on the gradient mapping criterion and fail to match the optimal sample complexities in unconstrained settings; 2) their analysis is exclusively applicable to non-convex functions, without considering convex and strongly convex objectives. To address these issues, we introduce novel projection-free variance reduction algorithms and analyze their complexities under different criteria. For gradient mapping, our complexities improve existing results and match the optimal rates for unconstrained problems. For the widely-used Frank-Wolfe gap criterion, we provide theoretical guarantees that align with those for single-level problems. Additionally, by using a stage-wise adaptation, we further obtain complexities for convex and strongly convex functions. Finally, numerical experiments on different tasks demonstrate the effectiveness of our methods.

Adaptive Variance Reduction for Stochastic Optimization under Weaker Assumptions

This paper explores adaptive variance reduction methods for stochastic optimization based on the STORM technique. Existing adaptive extensions of STORM rely on strong assumptions like bounded gradients and bounded function values, or suffer an additional $\mathcal{O}(\log T)$ term in the convergence rate. To address these limitations, we introduce a novel adaptive STORM method that achieves an optimal convergence rate of $\mathcal{O}(T^{-1/3})$ for non-convex functions with our newly designed learning rate strategy. Compared with existing approaches, our method requires weaker assumptions and attains the optimal convergence rate without the additional $\mathcal{O}(\log T)$ term. We also extend the proposed technique to stochastic compositional optimization, obtaining the same optimal rate of $\mathcal{O}(T^{-1/3})$. Furthermore, we investigate the non-convex finite-sum problem and develop another innovative adaptive variance reduction method that achieves an optimal convergence rate of $\mathcal{O}(n^{1/4} T^{-1/2} )$, where $n$ represents the number of component functions. Numerical experiments across various tasks validate the effectiveness of our method.

Efficient Sign-Based Optimization: Accelerating Convergence via Variance Reduction

Sign stochastic gradient descent (signSGD) is a communication-efficient method that transmits only the sign of stochastic gradients for parameter updating. Existing literature has demonstrated that signSGD can achieve a convergence rate of $\mathcal{O}(d^{1/2}T^{-1/4})$, where $d$ represents the dimension and $T$ is the iteration number. In this paper, we improve this convergence rate to $\mathcal{O}(d^{1/2}T^{-1/3})$ by introducing the Sign-based Stochastic Variance Reduction (SSVR) method, which employs variance reduction estimators to track gradients and leverages their signs to update. For finite-sum problems, our method can be further enhanced to achieve a convergence rate of $\mathcal{O}(m^{1/4}d^{1/2}T^{-1/2})$, where $m$ denotes the number of component functions. Furthermore, we investigate the heterogeneous majority vote in distributed settings and introduce two novel algorithms that attain improved convergence rates of $\mathcal{O}(d^{1/2}T^{-1/2} + dn^{-1/2})$ and $\mathcal{O}(d^{1/4}T^{-1/4})$ respectively, outperforming the previous results of $\mathcal{O}(dT^{-1/4} + dn^{-1/2})$ and $\mathcal{O}(d^{3/8}T^{-1/8})$, where $n$ represents the number of nodes. Numerical experiments across different tasks validate the effectiveness of our proposed methods.

Experimental Investigation on the Friction-induced Vibration with Periodic Characteristics in a Running-in Process under Lubrication

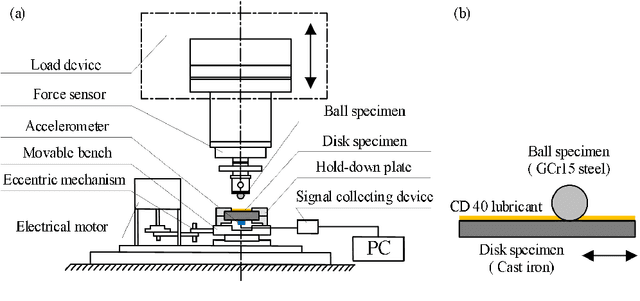
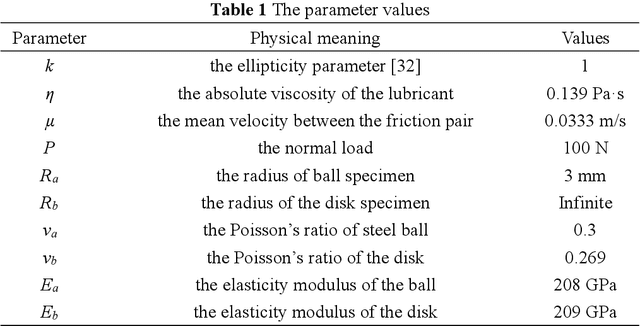
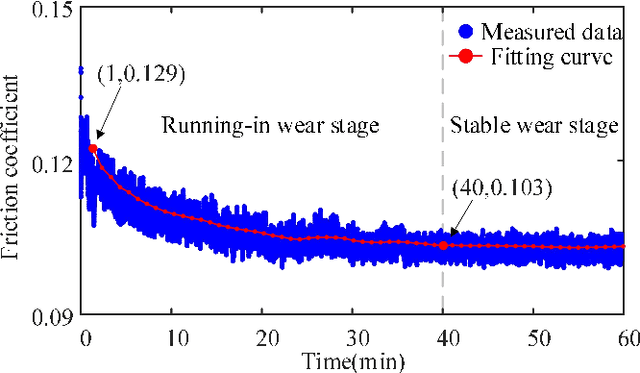
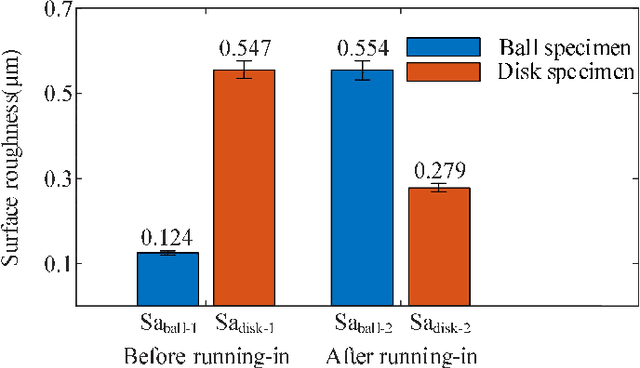
This paper investigated the friction-induced vibration (FIV) behavior under the running-in process with oil lubrication. The FIV signal with periodic characteristics under lubrication was identified with the help of the squeal signal induced in an oil-free wear experiment and then extracted by the harmonic wavelet packet transform (HWPT). The variation of the FIV signal from running-in wear stage to steady wear stage was studied by its root mean square (RMS) values. The result indicates that the time-frequency characteristics of the FIV signals evolve with the wear process and can reflect the wear stages of the friction pairs. The RMS evolvement of the FIV signal is in the same trend to the composite surface roughness and demonstrates that the friction pair goes through the running-in wear stage and the steady wear stage. Therefore, the FIV signal with periodic characteristics can describe the evolvement of the running-in process and distinguish the running-in wear stage and the stable wear stage of the friction pair.