Learning an Inventory Control Policy with General Inventory Arrival Dynamics

In this paper we address the problem of learning and backtesting inventory control policies in the presence of general arrival dynamics -- which we term as a quantity-over-time arrivals model (QOT). We also allow for order quantities to be modified as a post-processing step to meet vendor constraints such as order minimum and batch size constraints -- a common practice in real supply chains. To the best of our knowledge this is the first work to handle either arbitrary arrival dynamics or an arbitrary downstream post-processing of order quantities. Building upon recent work (Madeka et al., 2022) we similarly formulate the periodic review inventory control problem as an exogenous decision process, where most of the state is outside the control of the agent. Madeka et al. (2022) show how to construct a simulator that replays historic data to solve this class of problem. In our case, we incorporate a deep generative model for the arrivals process as part of the history replay. By formulating the problem as an exogenous decision process, we can apply results from Madeka et al. (2022) to obtain a reduction to supervised learning. Finally, we show via simulation studies that this approach yields statistically significant improvements in profitability over production baselines. Using data from an ongoing real-world A/B test, we show that Gen-QOT generalizes well to off-policy data.

MatFormer: Nested Transformer for Elastic Inference

Transformer models are deployed in a wide range of settings, from multi-accelerator clusters to standalone mobile phones. The diverse inference constraints in these scenarios necessitate practitioners to train foundation models such as PaLM 2, Llama, & ViTs as a series of models of varying sizes. Due to significant training costs, only a select few model sizes are trained and supported, limiting more fine-grained control over relevant tradeoffs, including latency, cost, and accuracy. This work introduces MatFormer, a nested Transformer architecture designed to offer elasticity in a variety of deployment constraints. Each Feed Forward Network (FFN) block of a MatFormer model is jointly optimized with a few nested smaller FFN blocks. This training procedure allows for the Mix'n'Match of model granularities across layers -- i.e., a trained universal MatFormer model enables extraction of hundreds of accurate smaller models, which were never explicitly optimized. We empirically demonstrate MatFormer's effectiveness across different model classes (decoders & encoders), modalities (language & vision), and scales (up to 2.6B parameters). We find that a 2.6B decoder-only MatFormer language model (MatLM) allows us to extract smaller models spanning from 1.5B to 2.6B, each exhibiting comparable validation loss and one-shot downstream evaluations to their independently trained counterparts. Furthermore, we observe that smaller encoders extracted from a universal MatFormer-based ViT (MatViT) encoder preserve the metric-space structure for adaptive large-scale retrieval. Finally, we showcase that speculative decoding with the accurate and consistent submodels extracted from MatFormer can further reduce inference latency.

Pareto Frontiers in Neural Feature Learning: Data, Compute, Width, and Luck

This work investigates the nuanced algorithm design choices for deep learning in the presence of computational-statistical gaps. We begin by considering offline sparse parity learning, a supervised classification problem which admits a statistical query lower bound for gradient-based training of a multilayer perceptron. This lower bound can be interpreted as a multi-resource tradeoff frontier: successful learning can only occur if one is sufficiently rich (large model), knowledgeable (large dataset), patient (many training iterations), or lucky (many random guesses). We show, theoretically and experimentally, that sparse initialization and increasing network width yield significant improvements in sample efficiency in this setting. Here, width plays the role of parallel search: it amplifies the probability of finding "lottery ticket" neurons, which learn sparse features more sample-efficiently. Finally, we show that the synthetic sparse parity task can be useful as a proxy for real problems requiring axis-aligned feature learning. We demonstrate improved sample efficiency on tabular classification benchmarks by using wide, sparsely-initialized MLP models; these networks sometimes outperform tuned random forests.

Scaling Laws for Imitation Learning in NetHack

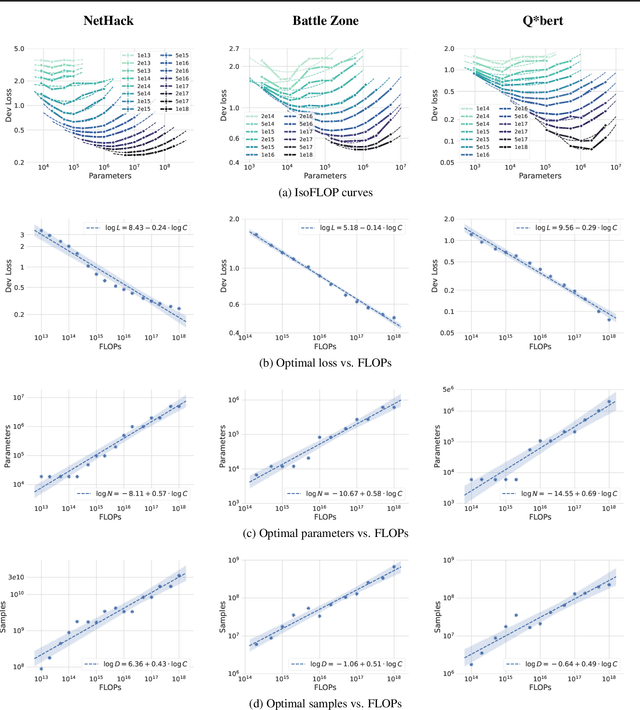
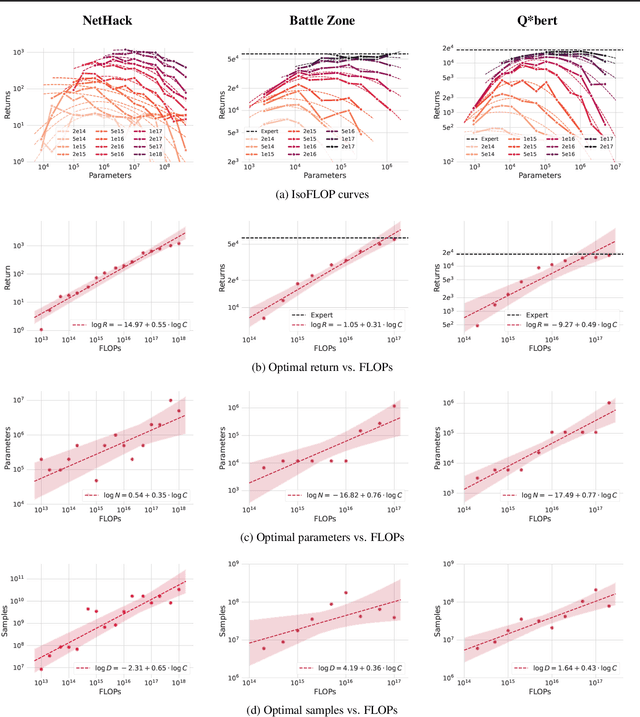
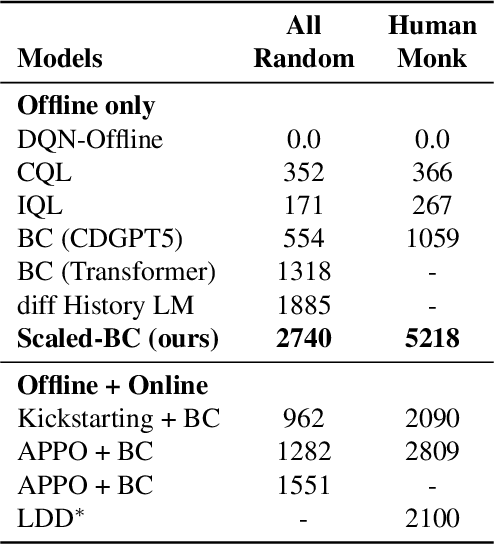
Imitation Learning (IL) is one of the most widely used methods in machine learning. Yet, while powerful, many works find it is often not able to fully recover the underlying expert behavior. However, none of these works deeply investigate the role of scaling up the model and data size. Inspired by recent work in Natural Language Processing (NLP) where "scaling up" has resulted in increasingly more capable LLMs, we investigate whether carefully scaling up model and data size can bring similar improvements in the imitation learning setting. To demonstrate our findings, we focus on the game of NetHack, a challenging environment featuring procedural generation, stochasticity, long-term dependencies, and partial observability. We find IL loss and mean return scale smoothly with the compute budget and are strongly correlated, resulting in power laws for training compute-optimal IL agents with respect to model size and number of samples. We forecast and train several NetHack agents with IL and find they outperform prior state-of-the-art by at least 2x in all settings. Our work both demonstrates the scaling behavior of imitation learning in a challenging domain, as well as the viability of scaling up current approaches for increasingly capable agents in NetHack, a game that remains elusively hard for current AI systems.

Beyond Implicit Bias: The Insignificance of SGD Noise in Online Learning

The success of SGD in deep learning has been ascribed by prior works to the implicit bias induced by high learning rate or small batch size ("SGD noise"). While prior works that focused on offline learning (i.e., multiple-epoch training), we study the impact of SGD noise on online (i.e., single epoch) learning. Through an extensive empirical analysis of image and language data, we demonstrate that large learning rate and small batch size do not confer any implicit bias advantages in online learning. In contrast to offline learning, the benefits of SGD noise in online learning are strictly computational, facilitating larger or more cost-effective gradient steps. Our work suggests that SGD in the online regime can be construed as taking noisy steps along the "golden path" of the noiseless gradient flow algorithm. We provide evidence to support this hypothesis by conducting experiments that reduce SGD noise during training and by measuring the pointwise functional distance between models trained with varying SGD noise levels, but at equivalent loss values. Our findings challenge the prevailing understanding of SGD and offer novel insights into its role in online learning.

AdANNS: A Framework for Adaptive Semantic Search

Web-scale search systems learn an encoder to embed a given query which is then hooked into an approximate nearest neighbor search (ANNS) pipeline to retrieve similar data points. To accurately capture tail queries and data points, learned representations typically are rigid, high-dimensional vectors that are generally used as-is in the entire ANNS pipeline and can lead to computationally expensive retrieval. In this paper, we argue that instead of rigid representations, different stages of ANNS can leverage adaptive representations of varying capacities to achieve significantly better accuracy-compute trade-offs, i.e., stages of ANNS that can get away with more approximate computation should use a lower-capacity representation of the same data point. To this end, we introduce AdANNS, a novel ANNS design framework that explicitly leverages the flexibility of Matryoshka Representations. We demonstrate state-of-the-art accuracy-compute trade-offs using novel AdANNS-based key ANNS building blocks like search data structures (AdANNS-IVF) and quantization (AdANNS-OPQ). For example on ImageNet retrieval, AdANNS-IVF is up to 1.5% more accurate than the rigid representations-based IVF at the same compute budget; and matches accuracy while being up to 90x faster in wall-clock time. For Natural Questions, 32-byte AdANNS-OPQ matches the accuracy of the 64-byte OPQ baseline constructed using rigid representations -- same accuracy at half the cost! We further show that the gains from AdANNS translate to modern-day composite ANNS indices that combine search structures and quantization. Finally, we demonstrate that AdANNS can enable inference-time adaptivity for compute-aware search on ANNS indices built non-adaptively on matryoshka representations. Code is open-sourced at https://github.com/RAIVNLab/AdANNS.

Modified Gauss-Newton Algorithms under Noise

Gauss-Newton methods and their stochastic version have been widely used in machine learning and signal processing. Their nonsmooth counterparts, modified Gauss-Newton or prox-linear algorithms, can lead to contrasting outcomes when compared to gradient descent in large-scale statistical settings. We explore the contrasting performance of these two classes of algorithms in theory on a stylized statistical example, and experimentally on learning problems including structured prediction. In theory, we delineate the regime where the quadratic convergence of the modified Gauss-Newton method is active under statistical noise. In the experiments, we underline the versatility of stochastic (sub)-gradient descent to minimize nonsmooth composite objectives.

Provable Copyright Protection for Generative Models

There is a growing concern that learned conditional generative models may output samples that are substantially similar to some copyrighted data $C$ that was in their training set. We give a formal definition of $\textit{near access-freeness (NAF)}$ and prove bounds on the probability that a model satisfying this definition outputs a sample similar to $C$, even if $C$ is included in its training set. Roughly speaking, a generative model $p$ is $\textit{$k$-NAF}$ if for every potentially copyrighted data $C$, the output of $p$ diverges by at most $k$-bits from the output of a model $q$ that $\textit{did not access $C$ at all}$. We also give generative model learning algorithms, which efficiently modify the original generative model learning algorithm in a black box manner, that output generative models with strong bounds on the probability of sampling protected content. Furthermore, we provide promising experiments for both language (transformers) and image (diffusion) generative models, showing minimal degradation in output quality while ensuring strong protections against sampling protected content.

Recurrent Convolutional Neural Networks Learn Succinct Learning Algorithms

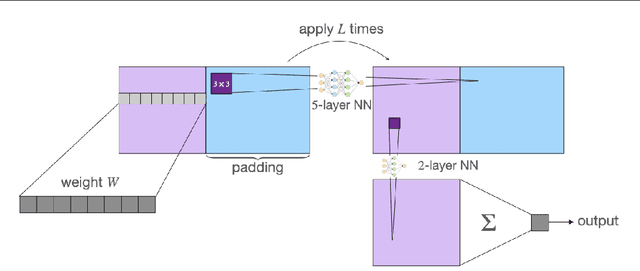
Neural Networks (NNs) struggle to efficiently learn certain problems, such as parity problems, even when there are simple learning algorithms for those problems. Can NNs discover learning algorithms on their own? We exhibit a NN architecture that, in polynomial time, learns as well as any efficient learning algorithm describable by a constant-sized learning algorithm. For example, on parity problems, the NN learns as well as row reduction, an efficient algorithm that can be succinctly described. Our architecture combines both recurrent weight-sharing between layers and convolutional weight-sharing to reduce the number of parameters down to a constant, even though the network itself may have trillions of nodes. While in practice the constants in our analysis are too large to be directly meaningful, our work suggests that the synergy of Recurrent and Convolutional NNs (RCNNs) may be more powerful than either alone.

Hidden Progress in Deep Learning: SGD Learns Parities Near the Computational Limit

There is mounting empirical evidence of emergent phenomena in the capabilities of deep learning methods as we scale up datasets, model sizes, and training times. While there are some accounts of how these resources modulate statistical capacity, far less is known about their effect on the computational problem of model training. This work conducts such an exploration through the lens of learning $k$-sparse parities of $n$ bits, a canonical family of problems which pose theoretical computational barriers. In this setting, we find that neural networks exhibit surprising phase transitions when scaling up dataset size and running time. In particular, we demonstrate empirically that with standard training, a variety of architectures learn sparse parities with $n^{O(k)}$ examples, with loss (and error) curves abruptly dropping after $n^{O(k)}$ iterations. These positive results nearly match known SQ lower bounds, even without an explicit sparsity-promoting prior. We elucidate the mechanisms of these phenomena with a theoretical analysis: we find that the phase transition in performance is not due to SGD "stumbling in the dark" until it finds the hidden set of features (a natural algorithm which also runs in $n^{O(k)}$ time); instead, we show that SGD gradually amplifies a Fourier gap in the population gradient.